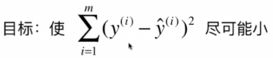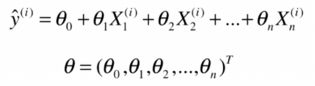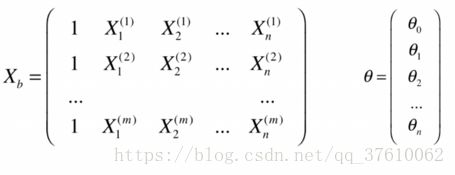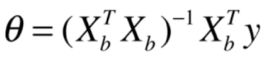多元线性回归算法学习笔记

多元线性回归的思路

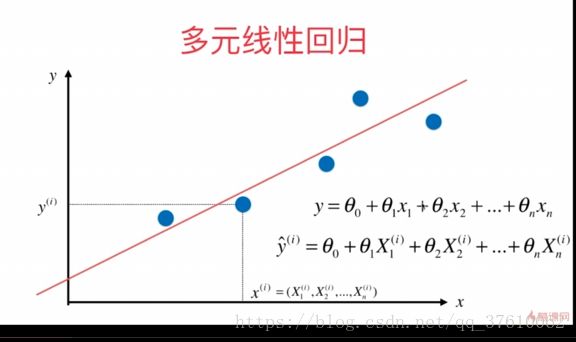
和简单线性回归相比 x 由一个特征，变为一个向量 X，含有多个特征。

找出一条直线（多维度实际不是直线，只是为了形象描述），最大程度的拟合 所有的点；

直线的方程是  ，X ， 和Y都是已知的，只需要求出 每一个 即可，所求的也是一个向量；

思路：

和简单线性回归一样，让预测结果和真实的结果的差值的平方 尽可能的小；

方法：

先看  ，中的实际为一个行向量，首先将转置为一个列向量 ；

然后对 的式子做一点改变： 在  前也乘一个系数  ，但是不改变原式子，所以让  1。

 

所以 就变成了：

 

因此，显而易见的  就可以写成两个向量的点乘：

然后把这个式子推广到整个的  和  中：

其中  和  为：

 

即 原来的矩阵 在第一列加了一个元素全部为1 的列向量，是（m,n）的矩阵，所以 为（m,n+1）的矩阵；

 即我们需要求的所有组成的矩阵（每个X前的系数，和一个截距），一共有n 个X（特征），再加一个截距，所以是一个（n+1,1）的矩阵。

所得结果：为 所有的预测值组成的向量 ；

所以这是一个矩阵的乘法所得到的结果，是一个(m , n+1)的矩阵，是一个(n+1,1)的矩阵；（矩阵的乘法的规则，的每一行的元素和的每一列的元素相乘再相加得到结果，是一个（m , 1）的矩阵）

将 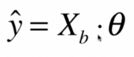 带入目标函数，并将目标函数向量化：  

在目标函数中，对第一个 进行了转置，这是为了方便使用矩阵的乘法；转置之后，第一个式子为（1，m）的行向量，第二个式子为（m,1）的列向量；所以最终结果为一个值。

目标函数中 和 都是已知的，所以只需要求出 即可；的推导在这里不讨论

多元线性回归的正规方程解（Normal Equation）:

缺点：时间复杂度高：O(n^3) (优化O(n^2.4))； 当我们有上百万个样本，或者上百万个特征的时候，运算时间会非常长；但是能直接求得数学解也是很不错的，因为在机器学习算法中，很少有算法可以直接求出数学解。

优点：不需要对数据做归一化处理；结果是 原始数据运算得到结果，所以不存在量纲的问题；

编写一个自己的LinearRegression 的算法：

注意：

求矩阵的逆矩阵的方法： 

np.linalg.inv()

将两个矩阵在水平方向上堆叠起来的方法：

np.hstack([矩阵1,矩阵2]

具体代码如下：

import numpy as np
class LinearRegression():

    def __init__(self):
        '''初始化Linear Regression 模型'''
        self.coef_ = None
        self.interception_ = None
        self._theta = None

    def fit_normal(self , X_train , y_train):

        assert X_train.shape[0] == y_train.shape[0]

        X_b = np.hstack([np.ones((len(X_train), 1)),X_train])


        ##
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.coef_ = self._theta[1:]
        self.interception_ = self._theta[0]

        return self

    def predict(self, X_predict):
        assert self.interception_ is not None and self.coef_ is not None
        assert X_predict.shape[1] == len(self.coef_.shape)

        X_b = np.hstack([np.ones((len(X_predict), 1)),X_predict])
        return X_b.dot(self._theta)

    def score(self,X_test ,y_test):
        assert self.interception_ is not None and self.coef_ is not None
        y_predict = self.predict(X_test)
        r2_score = 1-  (np.sum((y_test-y_predict)**2)/len(y_test))/np.var(y_test)
        return r2_score


    def __repr__(self):
        return 'LinearRegression()'