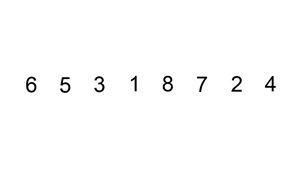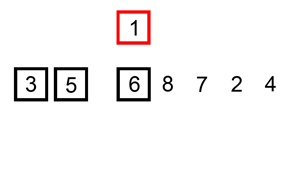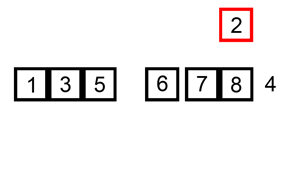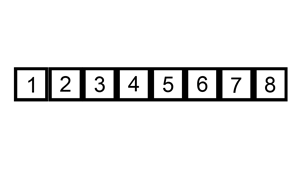Java中的数据结构和算法快速学习

Java中的数据结构和算法

在Java软件开发工程师（SDE）的面试过程中非常有用。

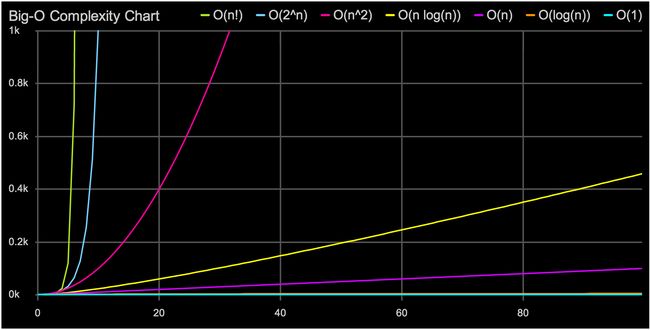
大O符号

Big-O复杂性图表

常量 - 语句（一行代码）

a + =  1 ;

增长率：1

对数 - 分为两半（二分搜索）

而（n >  1）{ 
  n = n /  2 ; 
}

增长率：log（n）

线性 - 循环

for（int i =  0 ; i < n; i ++）{
   // statement 
  a + =  1 ; 
}

增长率：n

循环执行N时间，因此语句序列也执行N时间。如果我们假设语句是O(1)，则for循环的总时间N * O(1)是O(N)整体。

二次 - 有效的排序算法

Mergesort, Quicksort, …

增长率：n * log（n）

二次 - 双循环（嵌套循环）

for（int c =  0 ; c < n; c ++）{
   for（int i =  0 ; i < n; i ++）{
     //语句序列 
    a + =  1 ; 
  } 
}

增长率：n ^ 2

外循环执行N次。每次外循环执行时，内循环执行M次数。结果，内循环中的语句总共执行一次N * M。因此，复杂性是O(N * M)。在一个常见的特殊情况下，内循环的停止条件J < N代替J < M（即内循环也执行N时间），两个循环的总复杂度是O(N2)。

立方 - 三重循环

for（c =  0 ; c < n; c ++）{
   for（i =  0 ; i < n; i ++）{
     for（x =  0 ; x < n; x ++）{ 
      a + =  1 ; 
    } 
  } 
}

增长率：n ^ 3

指数 - 穷举搜索

Trying to break a password generating all possible combinations

增长率：2 ^ n

IF-THEN-ELSE

if（cond）{ 
  block 1（statement of statements）
} else { 
  block 2（statement of statements）
}

如果block 1采取O(1)和block 2采取O(N)，if-then-else声明将是O(N)。

带有函数/过程调用的语句

当语句涉及函数/过程调用时，语句的复杂性包括函数/过程的复杂性。假设您知道函数/过程f需要恒定时间，并且该函数/过程g需要与其参数值成比例（线性输入）的时间k。然后，下面的陈述表明时间复杂。

f(k)已经O(1) g(k)有O(k)

涉及循环时，适用相同的规则。例如：

for J in 1 .. N loop
  g(J);
end loop;

有复杂性(N2)。循环执行N次，每个函数/过程调用g(N)都很复杂O(N)。

算法

简单的排序

冒泡排序

示例代码

泡泡排序非常慢，但它在概念上是最简单的排序算法。

排序过程

1. 比较两个项目。
2. 如果左边的那个更大，则交换它们。
3. 向右移动一个位置。

效率

对于10数据项，这是45比较（9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1）。

通常，N数组中的项目数在哪里，N-1第一遍，N-2第二遍，等等都有比较。对于这样的一系列的总和的公式是 (N–1) + (N–2) + (N–3) + ... + 1 = N*(N–1)/2 N*(N–1)/2 is 45 (10*9/2)当N是10。

选择排序

示例代码

简单学习

选择排序通过减少必要从交换次数上冒泡排序提高O(N2)到O(N)。不幸的是，比较的数量仍然存在O(N2)。但是，选择排序仍然可以为必须在内存中物理移动的大型记录提供显着改进，从而导致交换时间比比较时间更重要。

效率

选择排序执行与冒泡排序相同数量的比较：N*(N-1)/2。对于10数据项，这是45比较。但是，10项目需要少于10掉期。对于100项目，4,950需要进行比较，但少于100交换。对于较大的值N，比较时间将占主导地位，因此我们不得不说选择排序在O(N2)时间上运行，就像冒泡排序一样。

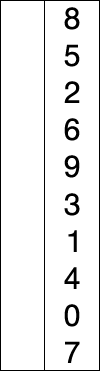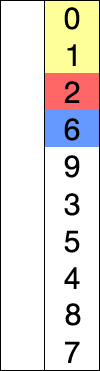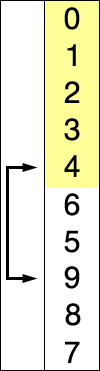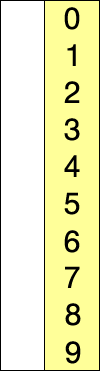
插入排序

示例代码

简单的解释

在大多数情况下，插入排序是本章所述的基本排序中最好的。它仍然可以O(N2)及时执行，但它的速度大约是冒泡排序的两倍，并且比正常情况下的选择排序快一些。它也不是太复杂，虽然它比泡沫和选择的排序稍微多一些。它经常被用作更复杂的排序的最后阶段，例如quicksort。

效率

这个算法需要多少次比较和复制？在第一次传递时，它比较最多一个项目。在第二次传球时，最多两个项目，依此类推，最后一次传球最多可进行N-1次比较。这是1 + 2 + 3 + ... + N-1 = N*(N-1)/2

但是，因为在每次传递时，在找到插入点之前实际比较了最大项目数的一半的平均值，我们可以除以2，这给出了 N*(N-1)/4

副本数量与比较数量大致相同。但是，副本不像交换那样耗费时间，因此对于随机数据，此算法的运行速度是冒泡排序的两倍，并且比选择排序的速度快。

在任何情况下，与本章中的其他排序例程一样，插入排序会O(N2)及时运行随机数据。

对于已经排序或几乎排序的数据，插入排序的效果要好得多。当数据按顺序排列时，while循环中的条件永远不会为真，因此它将成为外循环中的一个简单语句，它执行N-1时间。在这种情况下，算法O(N)及时运行。如果数据几乎已经排序，插入排序几乎可以在几乎O(N)一段时间内运行，这使得它成为一种简单而有效的方式来订购一个只是稍微乱序的文件。

高级排序

合并排序

示例代码

简单的解释

mergesort是一种比我们在“简单排序”中看到的更有效的排序技术，至少在速度方面。虽然泡沫，插入和选择排序需要花费O(N2)时间，但mergesort却是O(N*logN)。

例如，如果N（要排序的项目数）是10,000，则N2是100,000,000，而N*logN仅是40,000。如果40使用mergesort 对这么多项进行排序需要几秒钟，那么28插入排序几乎需要几个小时。

mergesort也很容易实现。它在概念上比快速排序更容易，壳牌更短。

mergesort算法的核心是两个已经排序的数组的合并。合并两个已排序的数组A并B创建第三个数组，C其中包含和的所有元素，A并按B排序顺序排列。

与quicksort类似，应该排序的元素列表分为两个列表。这些列表独立排序然后组合。在列表组合期间，元素被插入（或合并）在列表中的正确位置。

您将一半划分为两个季度，对每个季度进行排序，然后将它们合并以进行排序。

排序过程

1. 假设左数组的大小为k，右数组的大小为m，总数组的大小为n（= k + m）。
2. 创建一个大小为n的辅助数组
3. 将左数组的元素复制到辅助数组的左侧部分。这是位置0直到k-1。
4. 将右侧数组的元素复制到辅助数组的右侧部分。这是位置k直到m-1。
5. 创建索引变量i = 0; 并且j = k + 1
6. 循环遍历数组的左侧和右侧部分，并始终将最小值复制回原始数组。一旦i = k，所有值都被复制回原始数组。右数组的值已经到位。

效率

正如我们所指出的，mergesort及时运行O(N*logN)。存在24对8项目进行排序所需的副本。Log28是的3，8*log28等于24。这表明，对于8项目的情况，副本的数量是成比例的N*log2N。

在mergesort算法中，比较次数总是略小于副本数。

与Quicksort比较

与快速排序相比，mergesort算法在划分列表方面投入的精力更少，但更多地用于解决方案的合并。

Quicksort可以对现有集合进行“内联”排序，例如，它不必创建集合的副本，而标准mergesort确实需要数组的副本，尽管mergesort的（复杂）实现允许避免这种复制。

快速排序

示例代码

简单解释 简单说明2

Quicksort无疑是最受欢迎的排序算法，并且有充分的理由：在大多数情况下，它是最快的，O(N*logN)及时运行。（这仅适用于内部或内存中的排序;对于磁盘文件中的数据排序，其他算法可能更好。）

要了解quicksort，您应该熟悉分区算法。

Quicksort算法通过将数组分成两个子数组然后递归调用自身来快速分配这些子数组。

排序过程

预习

如果数组只包含一个元素或零元素，则对数组进行排序。

如果数组包含多个元素，则：

1. 从数组中选择一个元素。该元素称为“枢轴元素”。例如，选择数组中间的元素。
2. 所有小于枢轴元素的元素都放在一个数组中，所有较大的元素放在另一个数组中。
3. 通过递归地将Quicksort应用于它们来对两个数组进行排序。
4. 组合阵列。

Quicksort可以实现“就地”排序。这意味着排序发生在数组中，并且不需要创建其他数组。

效率

Quicksort O(N*logN)及时运作。分而治之算法通常都是如此，其中递归方法将一系列项目分成两组，然后调用自身来处理每个组。在这种情况下，对数实际上有一个基数2：运行时间与之成正比N*log2N。

标准Java数组排序

Java提供了一种使用标准排序数组的标准方法Arrays.sort()。这种排序算法是一种经过修改的快速排序，可以更频繁地显示出复杂性O(n log(n))。有关详细信息，请参阅Javadoc。

数据结构

堆栈

堆栈只允许访问一个数据项：插入的最后一项。如果删除此项，则可以访问插入的倒数第二个项目，依此类推。

堆栈也是应用于某些复杂数据结构的算法的便利辅助。在“二叉树”中，我们将看到它用于帮助遍历树的节点。

注意数据的顺序是如何反转的。因为推送的最后一个项目是第一个弹出的项目。

效率

可以在常量O(1)时间内从Stack类中实现的堆栈中推送和弹出项目。也就是说，时间不依赖于堆栈中有多少项，因此非常快。不需要进行比较或移动。

队列

队列是一种类似于堆栈的数据结构，除了在队列中插入的第一个项目是第一个要删除的项目（先进先出FIFO），而在堆栈中，就像我们一样看到，插入的最后一项是第一个被删除（LIFO）。

双端

双端队列是一个双端队列。您可以在任一端插入项目并从任一端删除它们。可以调用方法insertLeft()和insertRight()，removeLeft()和removeRight()。

优先级队列

优先级队列是比堆栈或队列更专业的数据结构。但是，它在令人惊讶的情况下是一个有用的工具。与普通队列一样，优先级队列具有前部和后部，并且项目从前部移除。但是，在优先级队列中，项目按键值排序，以便具有最低键（或在某些实现中为最高键）的项目始终位于前面。将物品插入适当的位置以维持订单。

效率

在我们在此处显示的优先级队列实现中，插入O(N)及时运行，而删除需要O(1)时间。

链接列表

阵列具有作为数据存储结构的某些缺点。在无序数组中，搜索速度很慢，而在有序数组中，插入速度很慢。在这两种数组中，删除速度很慢。此外，数组的大小在创建后无法更改。

我们将看一个解决其中一些问题的数据存储结构：链表。链接列表可能是数组之后第二常用的通用存储结构。

链接

在链表中，每个数据项都嵌入在链接中。链接是一个名为Link的类的对象。每个Link对象都包含列表中下一个链接的引用（通常称为next）。

LinkList类只包含一个数据项：对列表中第一个链接的引用。首先调用此引用。这是列表中唯一保留的关于任何链接位置的永久信息。它使用每个链接的下一个字段，通过首先跟随引用链来查找其他链接。

双端列表

双端列表类似于普通链表，但它还有一个附加功能：对最后一个链接以及第一个链接的引用。

对最后一个链接的引用允许您直接在列表末尾和开头插入新链接。当然，您可以在普通单端列表的末尾插入一个新链接，方法是遍历整个列表，直到结束，但这种方法效率很低。

访问列表末尾以及开头使得双端列表适用于单端列表无法有效处理的某些情况。一种这样的情况是实现队列; 我们将在下一节中看到这种技术的工作原理。

链表效率

在链表的开头插入和删除非常快。它们涉及仅更改一个或两个引用，这需要O(1)时间。

在特定项目旁边查找，删除或插入需要平均搜索列表中一半的项目。这需要O(N)比较。数组也O(N)适用于这些操作，但链接列表更快，因为插入或删除项目时不需要移动任何内容。效率的提高可能非常显着，特别是如果副本比比较需要更长的时间。

当然，链表相对于数组的另一个重要优点是链表使用了所需的内存，并且可以扩展以填充所有可用内存。

排序列表

在我们迄今为止看到的链表中，没有要求按顺序存储数据。但是，对于某些应用程序，在列表中按排序顺序维护数据很有用。具有此特征的列表称为排序列表。

在排序列表中，项目按键值按排序顺序排列。删除往往局限于最小（或最大）在列表中，这是在列表中的启动项，虽然有时find()和delete()方法，它通过列表中指定的链接进行搜索，也会被使用。

排序链表的效率

在排序的链表中插入和删除任意项需要O(N)进行比较（N/2平均），因为必须通过单步执行找到适当的位置。但是，可以及时找到或删除最小值，O(1)因为它位于列表的开头。如果应用程序经常访问最小项目，并且快速插入并不重要，那么排序链接列表是一种有效的选择。例如，优先级队列可以由排序的链表实现。

双重链接列表

让我们检查链表上的另一个变体：双向链表（不要与双端列表混淆）。双向链表的优势是什么？普通链表的一个潜在问题是难以沿列表向后遍历。像current = current.next这样的语句可以方便地进入下一个链接，但是没有相应的方法可以转到上一个链接。

双向链表提供此功能。它允许您向后遍历以及在列表中前进。秘诀是每个链接都有两个引用而不是一个链接。第一个是下一个链接，就像普通列表一样。第二个是上一个链接。

双重链接列表作为Deques的基础

双向链表可以用作双端队列的基础。在双端队列中，您可以在任一端插入和删除，双向链表提供此功能。

迭代器

包含对数据结构中的项的引用的对象（用于遍历这些结构）通常称为迭代器（或者有时，如某些Java类，枚举器）。

哈希表

一个重要的概念是如何将一系列键值转换为一系列数组索引值。在哈希表中，这是通过哈希函数完成的。但是，对于某些类型的密钥，不需要散列函数; 键值可以直接用作数组索引。

因此，我们寻找一种方式来挤压范围为0至超过7,000,000,000,000入范围0来100,000。一个简单的方法是使用模运算符（%），当一个数字除以另一个数时，它会找到余数：

arrayIndex = hugeNumber % arraySize;

这是散列函数的示例。它将大范围内的数字哈希（转换）为较小范围内的数字。

哈希效率

在哈希表中插入和搜索可以接近O(1)时间。如果不发生冲突，则只需调用哈希函数和单个数组引用即可插入新项或查找现有项。这是最短的访问时间。

 

十大面向对象设计原则

1. 保持代码干净（不要重复自己） - 避免代码重复
2. 封装了哪些细节 - 隐藏实现细节，有助于维护
3. 开放式封闭式设计原理 - 开放式扩展，关闭以进行修改
4. SRP（单一责任原则） - 一个班级应该做一件事，做得好
5. DIP（依赖倒置原则） - 不要问，让框架给你
6. 支持组合而不是继承 - 代码重用而不需要不灵活的代价
7. LSP（Liskov替换原则） - 子类型必须可替代超类型
8. ISP（Interface Segregation Pricinciple） - 避免monilithic接口，减少客户端的痛苦
9. 接口编程 - 有助于维护，提高灵活性
10. 授权原则 - 不要自己做所有事情，委托它

可以尝试的

1. 三角形数字
2. 堆排序，二进制搜索（BST）
3. 面向对象的设计。主要概念，是否需要使用模式？
4. 动态重新编译如何在Resin（或任何其他Java servlet容器）中工作
5. 写一个O（log（n））函数

参考

1. Java中的数据结构和算法，Robert Lafore的第二版
2. 10 Java程序员应该知道的面向对象设计原则
3. 设计模式
4. 傻瓜算法（第1部分）：Big-O表示法和排序
5. 大O符号
6. Big O表示法的初学者指南
7. 大O符号。使用无聊的数学来衡量代码的效率
8. 理解算法复杂度，渐近和Big-O表示法
9. Big-O算法复杂性备忘单
10. Java中的算法
11. Java中的Mergesort
12. Java中的Quicksort

本教程翻译自：https://github.com/donbeave/interview

转载需备注作者及出处