k-d tree算法原理及实现
k-d tree即k-dimensional tree,常用来作空间划分及近邻搜索,是二叉空间划分树的一个特例。通常,对于维度为k,数据点数为N的数据集,k-d tree适用于N≫2k的情形。
1)k-d tree算法原理
k-d tree是每个节点均为k维数值点的二叉树,其上的每个节点代表一个超平面,该超平面垂直于当前划分维度的坐标轴,并在该维度上将空间划分为两部分,一部分在其左子树,另一部分在其右子树。即若当前节点的划分维度为d,其左子树上所有点在d维的坐标值均小于当前值,右子树上所有点在d维的坐标值均大于等于当前值,本定义对其任意子节点均成立。
1.1)树的构建
一个平衡的k-d tree,其所有叶子节点到根节点的距离近似相等。但一个平衡的k-d tree对最近邻搜索、空间搜索等应用场景并非是最优的。
常规的k-d tree的构建过程为:循环依序取数据点的各维度来作为切分维度,取数据点在该维度的中值作为切分超平面,将中值左侧的数据点挂在其左子树,将中值右侧的数据点挂在其右子树。递归处理其子树,直至所有数据点挂载完毕。
a)切分维度选择优化
构建开始前,对比数据点在各维度的分布情况,数据点在某一维度坐标值的方差越大分布越分散,方差越小分布越集中。从方差大的维度开始切分可以取得很好的切分效果及平衡性。
b)中值选择优化
第一种,算法开始前,对原始数据点在所有维度进行一次排序,存储下来,然后在后续的中值选择中,无须每次都对其子集进行排序,提升了性能。
第二种,从原始数据点中随机选择固定数目的点,然后对其进行排序,每次从这些样本点中取中值,来作为分割超平面。该方式在实践中被证明可以取得很好性能及很好的平衡性。
本文采用常规的构建方式,以二维平面点(x,y)的集合(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)为例结合下图来说明k-d tree的构建过程。
a)构建根节点时,此时的切分维度为x,如上点集合在x维从小到大排序为(2,3),(4,7),(5,4),(7,2),(8,1),(9,6);其中值为(7,2)。(注:2,4,5,7,8,9在数学中的中值为(5 + 7)/2=6,但因该算法的中值需在点集合之内,所以本文中值计算用的是len(points)//2=3, points[3]=(7,2))
b)(2,3),(4,7),(5,4)挂在(7,2)节点的左子树,(8,1),(9,6)挂在(7,2)节点的右子树。
c)构建(7,2)节点的左子树时,点集合(2,3),(4,7),(5,4)此时的切分维度为y,中值为(5,4)作为分割平面,(2,3)挂在其左子树,(4,7)挂在其右子树。
d)构建(7,2)节点的右子树时,点集合(8,1),(9,6)此时的切分维度也为y,中值为(9,6)作为分割平面,(8,1)挂在其左子树。至此k-d tree构建完成。
上述的构建过程结合下图可以看出,构建一个k-d tree即是将一个二维平面逐步划分的过程。
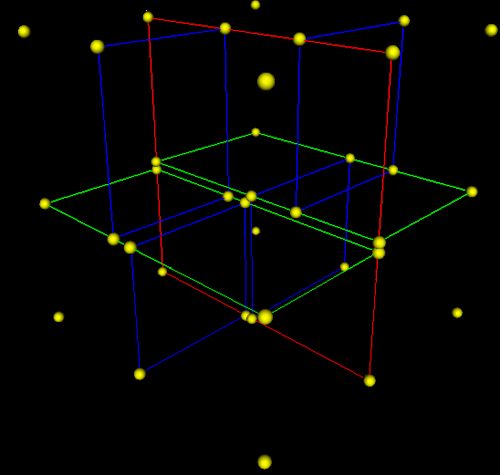
我们还可以结合下图(该图引自维基百科),从三维空间来看一下k-d tree的构建及空间划分过程。首先,边框为红色的竖直平面将整个空间划分为两部分,此两部分又分别被边框为绿色的水平平面划分为上下两部分。最后此4个子空间又分别被边框为蓝色的竖直平面分割为两部分,变为8个子空间,此8个子空间即为叶子节点。
2)最近邻搜索
给定点p,查询数据集中与其距离最近点的过程即为最近邻搜索。
如在上文构建好的k-d tree上搜索(3,5)的最近邻时,本文结合如下左右两图对二维空间的最近邻搜索过程作分析。
a)首先从根节点(7,2)出发,将当前最近邻设为(7,2),对该k-d tree作深度优先遍历。以(3,5)为圆心,其到(7,2)的距离为半径画圆(多维空间为超球面),可以看出(8,1)右侧的区域与该圆不相交,所以(8,1)的右子树全部忽略。
b)接着走到(7,2)左子树根节点(5,4),与原最近邻对比距离后,更新当前最近邻为(5,4)。以(3,5)为圆心,其到(5,4)的距离为半径画圆,发现(7,2)右侧的区域与该圆不相交,忽略该侧所有节点,这样(7,2)的整个右子树被标记为已忽略。
c)遍历完(5,4)的左右叶子节点,发现与当前最优距离相等,不更新最近邻。所以(3,5)的最近邻为(5,4)。
3)复杂度分析
| 操作 | 平均复杂度 | 最坏复杂度 |
| 新增节点 | O(logn) | O(n) |
| 删除节点 | O(logn) | O(n) |
| 最近邻搜索 | O(logn) | O(n) |
4)scikit-learn使用
scikit-learn是一个实用的机器学习类库,其有KDTree的实现。如下例子为直观展示,仅构建了一个二维空间的k-d tree,然后对其作k近邻搜索及指定半径的范围搜索。多维空间的检索,调用方式与此例相差无多。
# -*- coding: UTF-8 -*-
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.patches import Circle
from sklearn.neighbors import KDTree
np.random.seed(0)
points = np.random.random((100, 2))
tree = KDTree(points)
point = points[0]
# kNN
dists, indices = tree.query([point], k=3)
print(dists, indices)
# query radius
indices = tree.query_radius([point], r=0.2)
print(indices)