Matlab之山东大学数字图像处理实验三（图像滤波）

本文属于原创，转载请注明出处。

实验3.1：高斯滤波
实现图像的高斯滤波：
通过调整高斯函数的标准差(sigma)来控制平滑程度；
void Gaussian(const MyImage &input, MyImage &output, double sigma);
滤波窗口大小取为[6sigma-1]/22+1，[.]表示取整；
利用二维高斯函数的行列可分离性进行加速；
先对每行进行一维高斯滤波，再对结果的每列进行同样的一维高斯滤波；

实验3.2 快速均值滤波
实现图像的均值滤波
滤波窗口大小通过参数来指定：
void MeanFilter(const MyImage &input, MyImage &output, int window_size);
采用积分图进行加速，实现与滤波窗口大小无关的效率；

实验3.1：高斯滤波
高斯滤波

• 空间滤波=图像卷积
• 高斯滤波=以高斯函数为卷积核的图像卷积
• 
  二维高斯函数的公式如下所示：
  
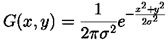
  根据题目要求，要根据输入的sigma创建二维高斯函数的卷积核，其中窗口大小的计算公式为：[6sigma-1]/22+1
  一开始我并没有注意到题目要求中的利用二维高斯函数的行列可分离性进行加速这一要求，先按照着自己的思路，就是先生成二维高斯函数的卷积核来进行高斯滤波：

生成高斯分布的卷积核的函数如下所示：

function[ kernal ] = getGaussian(sigma)
%用于生成符合高斯分布的卷积核
%   input_img为输入图像，sigma为标准差
%卷积核
n = round(6*sigma-1)/2*2+1;
%归一化的总值
h_sum = 0.0;
%卷积核的值
temp = 0.0;
%n*n的卷积核
kernal = zeros(n);
%卷积核的中心坐标
x = ceil(n/2);
y = ceil(n/2);
%display(x);
%根据高斯公式生成卷积核
for i = 1:n
    for j = 1:n
        distance = (i-x)^2+(j-y)^2;
        temp = exp((-distance)/2*sigma^2)/(2*pi*sigma^2);
        h_sum = h_sum + temp;
        kernal(i,j) = temp; 
    end
end
%display(kernal);
%归一化之后的卷积核
for i = 1:n
    for j = 1:n
        kernal(i,j) = kernal(i,j)/h_sum;
    end
end
%display(kernal);
end

其中要注意的就是要对卷积核进行归一化。

然后就是使用二维高斯滤波的函数：

function gaussian( input_img,sigma )
%   使用二维高斯滤波，效率低，耗时大概是40多倍
%   input_img是输入图像，output_img是输出图像，sigma是标准差
%计算运行时间
close;
tic;
%获取高斯滤波
kernal = getGaussian(sigma);
%获取高斯滤波的长宽
[kx,ky,dimension] = size(kernal);
%获取高斯滤波除中心点外的边界长度
k = floor(kx/2);
%获取输入图像的索引图像
[I,map] = imread(input_img);
input = imread(input_img);
subplot(1,2,1);
imshow(input),title('椒盐噪声的图片');
input = double(input);
%获取输入图像的长宽
[rows,cols,dimension] = size(I);

%初始化输出图像
output_img = uint8(zeros(rows,cols,dimension));
%边缘处理
for i = 1:k
    for j = 1:cols
        output_img(i,j,:) = input(i,j,:);
    end
end
for i = rows-k:rows
    for j = 1:cols
        output_img(i,j,:) = input(i,j,:);
    end
end
for j = 1:k
    for i = 1:rows
        output_img(i,j,:) = input(i,j,:);
    end
end
for j = cols-k:cols
    for i = 1:rows
        output_img(i,j,:) = input(i,j,:);
    end
end
%图像处理
for i = k+1:rows-k
    for j = k+1:cols-k
        %高斯滤波的每个权值之和
        temp_sum = 0.0;
        for ki = 1:kx
            for kj = 1:ky
                 temp_sum = temp_sum + input(i-k-1+ki,j-k-1+kj,:)*kernal(ki,kj);                     
            end
        end
        output_img(i,j,:) = temp_sum;
    end
end
subplot(1,2,2);
imshow(output_img),title('高斯滤波去噪结果');
imwrite(output_img,'gaussian.jpg');
toc;
end

这里提前对图片进行了加入椒盐噪声的处理，方便之后查看高斯滤波的处理效果。

P=imnoise(M,'gaussian',0.02)

总体思想就是获取高斯滤波的中心点，以及距离边界的长度，然后使用高斯滤波对原图进行每个相应像素点的加权计算，然后计算出该中心点处理后的值，这里要注意的是边缘处理，以及高斯滤波处理的都是原来的像素点的值，不能使用处理后的值，否则叠加起来误差会很大。

这个是二维高斯滤波的处理过程，它的执行时间大概在11s左右，非常耗时，不如将高斯滤波行列分离之后来得有效率。

下面介绍一下一维高斯滤波处理，核心思想是差不多的，就是将原来的二维高斯函数进行行列分离，然后先对行处理，然后再对结果的列进行处理，具体代码如下所示：

function gaussian2(input_img,sigma)
%   使用一维高斯滤波，效率高
%   input_img是输入图像，output_img是输出图像，sigma是标准差
%计算运行时间
close;
tic;
input = imread(input_img);
subplot(1,2,1);
imshow(input),title('椒盐噪声的图片');
input = double(input);
[rows,cols,dimension]=size(input);
%输出图像
output_img = uint8(zeros(rows,cols,dimension));
%卷积核
n = floor(6*sigma-1)/2*2+1;
%计算图象中心
k = floor((n+1)/2);
%存放一维高斯函数
gau = zeros(n);
sum = 0.0;
%二维高斯函数行列可分离成单个
for i  = 1:n
    gau(i)= exp(-((i-k).^2)/(2*sigma^2))/(sqrt(2*pi*sigma));
    sum = sum + gau(i);
end
%归一化
for i = 1:n  
    gau(i)=gau(i)/sum;
end

%卷积核中心到边界的距离
k = (n-1)/2;

%处理图片
%RGB三通道
R = input(:,:,1);
G = input(:,:,2);
B = input(:,:,3);
RR = uint8(zeros(rows,cols));
GG = uint8(zeros(rows,cols));
BB = uint8(zeros(rows,cols));
% x方向滤波
for y = 1:cols 
  for x = 1-k:rows-k  
        R_sum = 0;
        G_sum = 0;
        B_sum = 0;
        temp_sum = 0;  
        for i = -k:k             
            %判断是否在图像内部  
            if((i+x)>=1 && (i+x)<=rows)
                %单个通道的在x方向上一维高斯滤波中的值的总和
                R_sum = R_sum+(R(i+x,y) * gau(k+i+1));
                G_sum = G_sum+(G(i+x,y) * gau(k+i+1));
                B_sum = B_sum+(B(i+x,y) * gau(k+i+1));
                %一维高斯滤波的值得之和
                temp_sum = temp_sum + gau(k+i+1);  
            end
        end
        % x方向上的使用高斯滤波之后的结果
        RR(i+x,y) = R_sum/temp_sum;  
        GG(i+x,y) = G_sum/temp_sum;
        BB(i+x,y) = B_sum/temp_sum;
  end        
end  
% y方向滤波
for x = 1:rows 
  for y = 1-k:cols-k  
        R_sum = 0;
        G_sum = 0;
        B_sum = 0;
        temp_sum = 0;  
        for i = -k:k             
            %判断是否在图像内部  
            if((i+y)>=1 && (i+y)<=cols)
                %单个通道的在y方向上一维高斯滤波中的值的总和
                R_sum = R_sum+(RR(x,i+y) * gau(k+i+1));
                G_sum = G_sum+(GG(x,i+y) * gau(k+i+1));
                B_sum = B_sum+(BB(x,i+y) * gau(k+i+1));
                %一维高斯滤波的值得之和
                temp_sum = temp_sum + gau(k+i+1);  
            end
        end
        % y方向上的使用高斯滤波之后的最终结果
        R(x,i+y) = R_sum/temp_sum;  
        G(x,i+y) = G_sum/temp_sum;
        B(x,i+y) = B_sum/temp_sum;
  end        
end
%合成三通道
output_img(:,:,1) = R;
output_img(:,:,2) = G;
output_img(:,:,3) = B;
subplot(1,2,2);
imshow(output_img),title(['高斯滤波去噪结果,sigma为',num2str(sigma)]);
imwrite(output_img,'gaussian2.jpg');
toc;
end

这里要分成三通道进行处理，像之前那样一起处理不知道为啥不行。。。现在看一下两个函数的执行结果，并且进行比较一下：

加了椒盐噪声的图片：

二维高斯滤波：

gaussian('noise.jpg',0.8);

一维高斯滤波

gaussian2('noise.jpg',1.2);

很明显地能够看出来两种方式的执行效率上的不同，一维比二维快得多得多。

实验3.2 快速均值滤波
原理
积分图

• 图像I的积分图S是与其大小相同的图像，S的每一像素S(u,v)存贮的是I(u,v)左上角所有像素的颜色值之和。
  

• 积分图可增量计算，只需对原图进行一遍扫描：
  
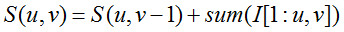
  基于积分图的快速均值滤波

• 设滤波窗口大小为2w+1，滤波结果为图像O，则：
  
  快速均值滤波第一步就是要计算积分图，计算积分图的时候要注意点（1,1），矩阵第一列进行单独的处理，保证积分图计算时不会出现矩阵越界的问题，然后再进行积分图的计算。
  然后根据积分图的快速均值滤波公式，由于中心点到边界的距离为w，所以我们还要对图像的边缘进行处理。
  具体的处理方法，根据积分图的愿意，可以用S(i,j)/(i*j)来表示。
  具体代码如下所示：

  function output_img = meanFilter(input_img,w)
  %   快速均值滤波
  %   input_img是输入图像，output_img是输出图像，w是窗口大小，但是之后要转化成2*size+1,保证为奇数
  close;
  input = imread(input_img);
  subplot(1,2,1);
  imshow(input),title('椒盐噪声的图片');
  [rows,cols,dimension]=size(input);
  %Z为像素个数
  Z = (2*w+1)*(2*w+1);
  %输出图像
  output_img = uint8(zeros(rows,cols,dimension));
  %三通道处理
  R = input(:,:,1);
  G = input(:,:,2);
  B = input(:,:,3);
  %积分图S的初始化
  SR = zeros(rows,cols);
  SG = zeros(rows,cols);
  SB = zeros(rows,cols);
  %S赋值
  SR(1,1) = R(1,1);
  SG(1,1) = G(1,1);
  SB(1,1) = B(1,1);
  %第一列赋值
  for i = 2:rows
      SR(i,1) = SR(1,1) + R(i,1);
      SG(i,1) = SR(1,1) + G(i,1);
      SB(i,1) = SR(1,1) + B(i,1);
  end
  %其余赋值
  for i = 1:rows
      for j = 2:cols
          SR(i,j) = SR(i,j-1) + sum(R(1:i,j));
          SG(i,j) = SG(i,j-1) + sum(G(1:i,j));
          SB(i,j) = SB(i,j-1) + sum(B(1:i,j));
      end
  end
  %边缘处理
  for i = 1:w+1
      for j = 1:cols
          output_img(i,j,1) = SR(i,j)/(i*j);
          output_img(i,j,2) = SG(i,j)/(i*j);
          output_img(i,j,3) = SB(i,j)/(i*j);
      end
  end
  for i = rows-w:rows
      for j = 1:cols
          output_img(i,j,1) = SR(i,j)/(i*j);
          output_img(i,j,2) = SG(i,j)/(i*j);
          output_img(i,j,3) = SB(i,j)/(i*j);
      end
  end
  for j = 1:w+1
      for i = 1:rows
          output_img(i,j,1) = SR(i,j)/(i*j);
          output_img(i,j,2) = SG(i,j)/(i*j);
          output_img(i,j,3) = SB(i,j)/(i*j);
      end
  end
  for j = cols-w:cols
      for i = 1:rows
          output_img(i,j,1) = SR(i,j)/(i*j);
          output_img(i,j,2) = SG(i,j)/(i*j);
          output_img(i,j,3) = SB(i,j)/(i*j);
      end
  end
  %滤波公式
  for i = w+2:rows-w
      for j = w+2:cols-w
          output_img(i,j,1) = (1/Z)*(SR(i+w,j+w)+SR(i-w-1,j-w-1)-SR(i+w,j-w-1)-SR(i-w-1,j+w));
          output_img(i,j,2) = (1/Z)*(SG(i+w,j+w)+SG(i-w-1,j-w-1)-SG(i+w,j-w-1)-SG(i-w-1,j+w));
          output_img(i,j,3) = (1/Z)*(SB(i+w,j+w)+SB(i-w-1,j-w-1)-SB(i+w,j-w-1)-SB(i-w-1,j+w));
      end
  end
  subplot(1,2,2);
  imshow(output_img),title('快速均值去噪后的图片');
  imwrite(output_img,'meanFilter.jpg');
  end
  
  
  

现在看看结果：

meanFilter('noise.jpg',5);

加了椒盐噪声的图片：

结果

可以看出边缘处理的还是比较有问题的，比较突兀，以后再接再厉！