Unity开发中常用的基础3D数学(向量,点乘,叉乘,矩阵,四元数,欧拉角)
在看了很多文章和书籍直后发现Unity中的数学知识是很重要的,想要做到游戏的高真实度和高流畅度,数学是必不可少的,今天就来记录一下基础的3D数学在Unity中开发时的运用,若文章中所写有不足,欢迎指出留言,互相交流,感谢!
转载请标注转载地址
一、Unity中的向量
向量这个词大家应该不陌生,在数学里向量就是一个方向,没有大小,同样,在Unity中我们可以根据向量去获取方向。比如说,我想把a物体移动到b物体所在的位置,那么首先我们要做的就是先确定我们前进的方向,在确立了方向之后,就可以按照我们想要的速度向b目标点移动了,Unity中使用向量的加法来实现物体位移,代码如下:
///
/// 向量的加法(从a位置移动到b位置)
///
public void Add()
{
//先计算二者方向
Vector3 dir = (target.position - cube.position).normalized;
//开始从a位置移动到b位置
cube.position = cube.position + dir * Time.deltaTime * 3;
}
其中,(target.forward - cube.forward)可以求得一个向量值,此处可以将该向量理解为有方向有大小的矢量,normalized表示该向量长度为1,向量没有大小,所以如果光是向量的话并不能完全表示朝向,将其大小设置为noemalized可以很好的表示出向量的朝向。
Unity中对于向量最好的一个例子是Vector3.Distance(),这个方法很常用,用来求得两个物体之间的距离,或者作为攻击范围等来使用,其实它的原理就是用两个向量相减求平方根得到的距离值,代码如下:
///
/// 向量的减法(计算a,b两物体间的距离)
///
public void Sub()
{
float dic = Vector3.Distance(cube.position, target.position);
print("距离为:" + dic);
}
二、向量的点乘和叉乘
很多地方出现过这么一句话:向量的点乘(Dot)判断角度,向量的叉乘(Cross)判断方向
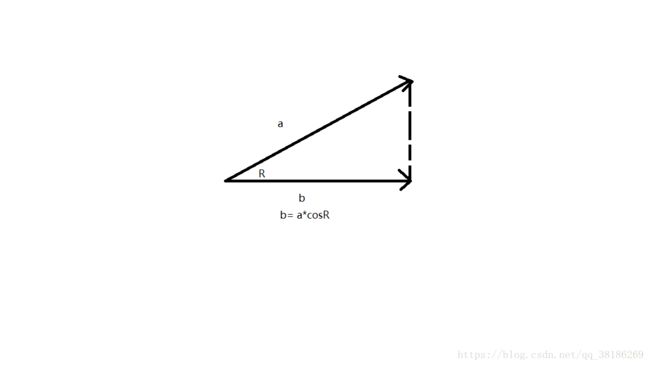
先说点乘,点乘在Unity中的使用是用来计算两个物体之间角度,用Vector2.Dot()或Vector3.Dot()方法可以得到一个弧度制,也就是这两个物体夹角的弧度值,可以使用Mathf.Acos(弧度制)*Rad2Deg来转换为夹角的角度值。对于点乘的理解2D的理解起来比较简单,数学中的勾股定理,当知道斜边长度为a,一条直角边长度为b,夹角为R,那么b = a*cosR,如下图所示:
叉乘判断方向,叉乘是两物体的法向量,举个例子,当我们的主角没有面对怪物时,我们可以先用点乘计算出当前主角的朝向和怪物当前朝向的角度,然后用叉乘我们可以判断出怪物是在我们的前?后?左?右?根据右手定则,当指向我们自己时,四指是逆时针,指向我们面朝方向时四指是顺时针,无论当前指向哪里,超过180度时都会变换朝向,所以叉乘时时刻刻都会告诉我们怎么转是最近的,Unity中我们用Vector3.Cross()计算两物体的叉乘,返回值是一个Vector3类型,最大为1最小为-1。我们可以用一个案例来理解点乘和叉乘:
public class SteeringWheelScript : MonoBehaviour {
private GameObject image;
private Vector3 imageTra;
//鼠标点向量
Vector3 mouseVec;
//上一帧鼠标点向量
Vector3 beforeMouseVec;
//鼠标点上一帧位置
Vector3 beforeMousePos;
private void Awake()
{
image = GameObject.Find("Canvas/Image");
imageTra = image.transform.position;
//beforeMousePos = imageTra;
}
///
/// 得到鼠标坐标
///
///
public Vector3 GetMousePos()
{
if (EventSystem.current.IsPointerOverGameObject()&&Input.GetMouseButton(0)&&!Input.GetMouseButtonUp(0))
{
return Input.mousePosition;
}
else
return default(Vector3);
}
///
/// 开始转动
///
public void TurnRun(Vector3 currentMousePos)
{
//得到向量
mouseVec = (currentMousePos - imageTra).normalized;
beforeMouseVec = (beforeMousePos - imageTra).normalized;
//计算方向
Vector3 direction = Vector3.Cross(beforeMousePos.normalized, beforeMouseVec.normalized);
print("方向:" + direction.z);
//计算角度
float radianValue = Vector3.Dot(beforeMouseVec.normalized, currentMousePos.normalized);//得到弧度值
float angleValue = Mathf.Acos(radianValue) * Mathf.Rad2Deg;//角度
print("角度:" + angleValue);
//顺时针转
if (direction.z > 0)
{
image.transform.eulerAngles = new Vector3(0,0, angleValue);
}
//逆时针
else if (direction.z < 0)
{
image.transform.eulerAngles = new Vector3(0, 0, -angleValue);
}
beforeMousePos = currentMousePos;
}
private void FixedUpdate()
{
TurnRun(GetMousePos());
}
}
这个是模拟方向盘的转动,这里我用的是UGUI,Unity版本是5.6,EventSystem.current.IsPointerOverGameObject()是用来判断当前鼠标是否在UI上面。
三、矩阵
矩阵在3D引擎底层实现中使用的非常多,对于矩阵,我们从固定流水线开始理解,固定流水线是指一个3D物体在显示器上成像的过程,在这个过程中就用到了非常多的矩阵转换。用一个比较好理解的方式来说吧,首先,当我们需要一个3D模型时,会让美工开始在3DMax里面制作,制作完成导出FBX格式,当前这个模型就是一个个体,也就是局部坐标,然后我们会把模型导入Unity中调整位置,进行拖拽,这个过程使得模型从单个个体变为了Unity中模型的其中之一,也就是世界坐标,此时我们要看到该模型,所以添加摄像机,把模型放在摄像机视野内,这样,又从世界坐标变成了观察坐标,当然,摄像机看不到的模型背面就会被优化掉,那么观察坐标就变成了裁剪坐标,之后为了把模型显示在屏幕上,又把裁剪坐标变为视口坐标,最后进行光栅化完成固定流水线。
以上是对矩阵的一个简单了解,物体的缩放,旋转,位移,虽然我们直接用Rotate等函数就可以很便捷的完成,但是其底层实现也是矩阵的变换,这里说一个小点,3D空间中,点是三维的,而矩阵是四维,这里涉及到了齐次坐标,进行矩阵计算时,会把三维的点转变成齐次坐标然后才可以计算,因为像位移,旋转,缩放等三维矩阵是完成不了的,点转为齐次坐标时会用1补齐第四位比如(x,y,z,1)
四、四元数
四元数在Unity中主要用于做旋转使用,这里说几个很常用的四元数方法,Quaternion.Eular()可以获取物体的四元数,Rotation就是一个四元数,但是不可以直接对它进行赋值,这里可以用到eularAngle 进行赋值,控制物体的旋转可以用AngleAxis()方法进行操作。
五、欧拉角
使用欧拉角进行旋转赋值时一定可能性会出现万向节死锁,什么是万向节死锁,其实万向节死锁的原因是欧拉角本身,欧拉角旋转赋值一般情况下是一对一,比如,旋转X轴,旋转Y轴,旋转Z轴,但是在一些情况下会变成一对多,比如旋转Z轴,X轴和Z轴进行了旋转使得整体旋转发生改变,X轴的旋转自由缺失,这种情况最好的避免方式是,仅对一个轴进行赋值,其余轴为0。直接使用欧拉角的代码效率还是比较高的。
到此Unity中比较常用的基础3D数学也就介绍完了,整体我是沿着在Unity开发中的使用来介绍的,如果大家对其中某些部分有兴趣可以去查阅一下资料,深挖一下。