TensorfFlow 实战Google深度学习框架读书笔记二:深层神经网络
1.激活函数
1.1线性模型的局限性
线性模型:
线性模型可以很好地解决线性可分问题。但在现实世界中,绝大部分的问题都是无法线性分割的。
深度学习为了更好地解决更加复杂的问题,而所谓复杂问题,至少是无法通过直线(或者高维空间的平面)划分的。
所以我们在深层神经网络中使用激活函数。
1.2激活函数去线性化
三种常用激活函数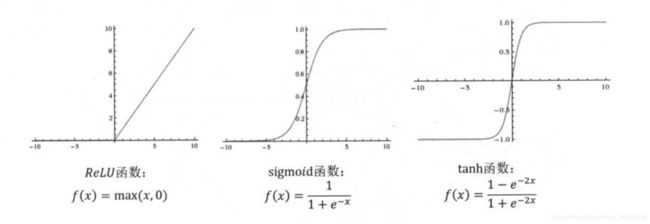
tensorflow提供了7中不同的非线性激活函数,tf.nn.relu、tf.sigmoid、tf.tanh是其中比较常用的几个。
例如前向传播算法使用relu
a = tf.nn.relu(tf.matmul(x,w1)+biases1)
y = tf.nn.relu(tf.matmul(a,w2)+biases2)
2.损失函数
2.1经典损失函数
交叉熵:用来判断输出向量和期望向量的距离。
给定两个概率分布p和q,通过q来表示p的交叉熵为:
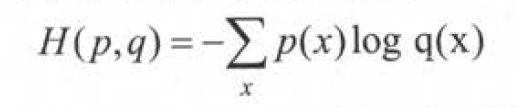
交叉熵刻画的是两个概率分布之间的距离,然而神经网络的输出却不一定是一个概率分布。
如何将神经网络前向传播得到的结果也变成概率分布呢?Sofmax回归就是一个非常常用的方法。
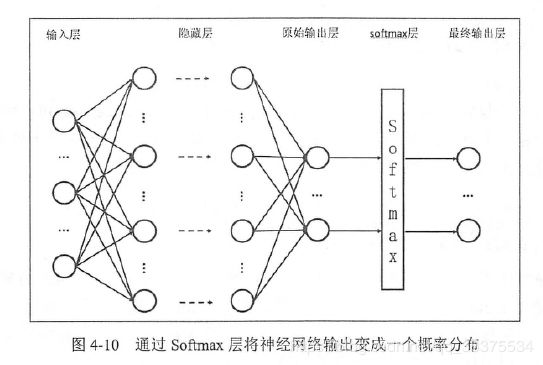
假设原始神经网络输出为y1,y2,…yn,那么经过softmax回归处理之后的输出为

当交叉熵作为神经网络的损失函数时,p代表的是正确答案,q代表的是预测值。

从直观上可以很容易地知道第二个预测答案要优于第一个。通过交叉熵计算得到的结果也是一致的(第二个交叉熵的值更小)。
代码实现如下
cross_entropy=-tf.reduce_mean(y_*tf.log(tf.clip_by_value(y,1e-10,1.0)))
#y_代表正确结果,y代表预测结果
上述过程包含了4个不同的tensorflow运算。
- tf.clip_by_value
可以将一个张量中的数值限制在一个范围之内,这样可以避免一些运算错误(比如log0是无效的)。
import tensorflow as tf
v=tf.constant([[1.0,2.0,3.0],[4.0,5.0,6.0]])
y=tf.clip_by_value(v,2.5,4.5)
sess = tf.Session()
print(sess.run(y))
sess.close()
输出
[[2.5 2.5 3. ]
[4. 4.5 4.5]]
- tf.log
底数为自然底数e(约等于2.718)
import tensorflow as tf
import math
v=tf.constant([[math.exp(1),math.exp(10),2.718]])
y=tf.log(v)
sess = tf.Session()
print(sess.run(y))
sess.close()
输出
[[ 0.99999994 10. 0.9998963 ]]
- 元素相乘*
与矩阵乘法tf.matmul不同,是元素之间直接相乘。
import tensorflow as tf
v1 = tf.constant([[1.0,2.0],[3.0,4.0]])
v2 = tf.constant([[5.0,6.0],[7.0,8.0]])
sess = tf.Session()
print(sess.run(v1*v2))
print(sess.run(tf.matmul(v1,v2)))
sess.close()
输出
[[ 5. 12.]
[21. 32.]]
[[19. 22.]
[43. 50.]]
- tf.reduce_mean
对整个矩阵做平均
import tensorflow as tf
v1 = tf.constant([[1.0,2.0,3.0],[4.0,5.0,6.0]])
sess = tf.Session()
with sess.as_default():
print(tf.reduce_mean(v1).eval())
输出
3.5
因为交叉熵一般会与softmax回归一起使用,所以tensorflow对这两个函数进行了统一封装,即:
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=y,labels=y_)
y为神经网络输出结果,y_为标准答案。
上述为分类问题,回归问题则不同。
均方误差(MSE)
均方误差一般应用于回归问题,解决回归问题的神经网络一般只有一个输出节点,这个节点的输出值就是预测值。

其中yi为一个batch中第i个数据的正确答案,而yi’为神经网络给出的预测值。
mse=tf.reduce_mean(tf.square(y_-y))
其中y代表神经网络的输出答案,y_代表标准答案。
2.2经典损失函数
tf.greater(a,b),比较a是否大于b。
tf.where(a,b,c):a为ture为b,否则为c。
import tensorflow as tf
a = tf.constant([1,2,3,4])
b = tf.constant([0,3,4,1])
sess = tf.InteractiveSession()
print(tf.greater(a,b).eval())
print(tf.where(tf.greater(a,b),a,b).eval())
输出
[ True False False True]
[1,3,4,4]
3.优化算法
梯度下降算法主要用于优化单个参数的取值。
反向传播算法给出了一个高效的方式在所有参数上使用梯度下降算法。
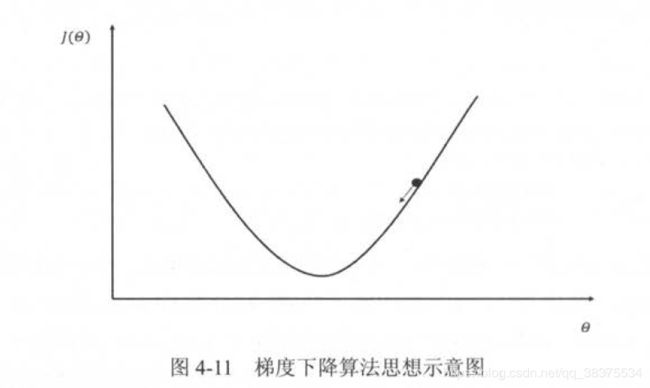
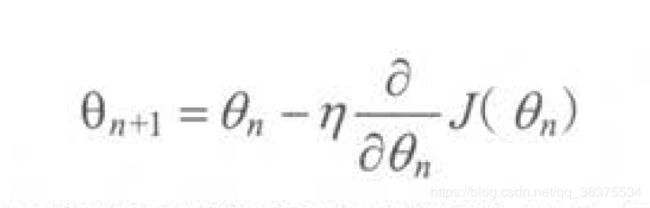
n为学习率
在海量训练数据下,要计算所有训练数据的损失函数是非常消耗时间的。为了加速训练过程,可以使用随机梯度下降的算法(SGD)。每次优化的是某一条数据上的损失函数,而不是全部训练数据上的损失函数。但是同时存在问题:在某一条数据上损失函数更小并不能代表全部数据上损失函数更小。
综上,在实际中使用这两种方式的折中–每次计算一小部分训练数据(batch)的损失函数。
神经网络训练过程大致如下:
batch_size=n
#每次读取一小部分数据
x=tf.placeholder(tf.float32,shape=(batch_size,2),name='x-input')
y_=tf.placeholder(tf.float32,shape=(batch_size,1),name='y-input')
#定义神经网络结构和优化算法
loss=...
train_step=tf.train.AdamOptimizer(0.001).minimize(loss)
#训练神经网络
with tf.Session()as sess
#参数初始化
...
#迭代的更新参数
for i in range(STEPS):
#准备batch_size个训练数据。一般将所有训练数据随机打乱之后再选取可以得到更好的优化效果
current_X,current_Y=...
sess.run(train_step,feed_dict={x:current_X,y_:current_Y})
4.学习率的设置
tensorflow提供了一中灵活的学习率设置方法----指数衰减法
tf.train_exponential_decay函数实现了指数衰减学习率
它实现了以下代码的功能:
decayed_learning_rate_base=learning_rate*decay_rate^(global_step/decay_steps)
decayed_learning_date:当前学习率
learning_rate_base:初始学习率
decay_rate:衰减速率
global_step:当前是第几次训练
decay_steps:通常表示完整的使用一边训练数据所需的迭代次数,也就是总样本数/batch
tf.train_exponential_decay函数的使用
import tensorflow as tf
global_step = tf.Variable(0)
#生成学习率
learning_rate = tf.train.exponential_decay(0.1,global_step,100,0.96,staircase=True)
#在minimize函数中传入global_step将自动更新global_step参数,从而更新学习率
learn_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(..my loss..,global_step=global_step)
上段代码设定了初始学习率为0.1,指定了staircase=True,所以每训练100轮后学习率乘以0.96.
tf.train_exponential_decay中staircase参数:默认为False,这时学习率变化曲线如灰色曲线所示;当为True时,学习率为阶梯状,表示一个batch的学习率一样,global_step/decay_steps会被转化为整数。
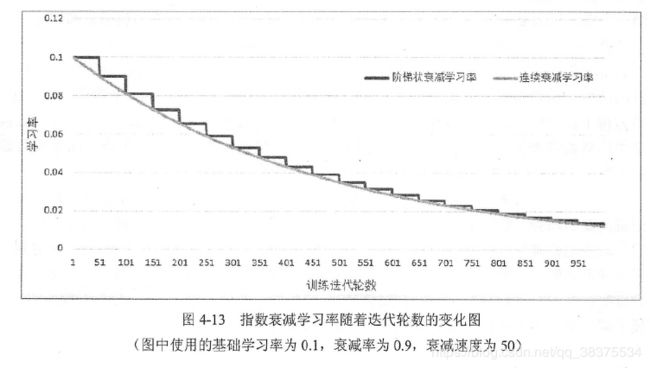
之所以这样设置,是为了让学习率既可以每次训练后都变化,也可以一个batch后再变化。
5.过拟合问题
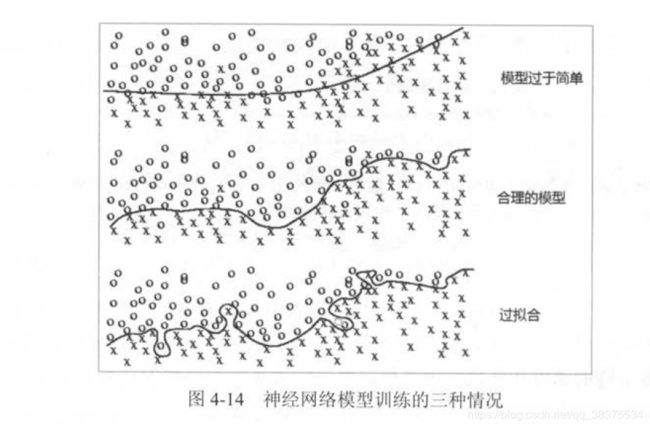
为了避免过拟合,一个常用的方法是正则化(regularization)。正则化的思想就是在损失函数中加入刻画模型复杂程度的指标。
![]()
其中R(w)刻画的是模型复杂度,λ表示模型复杂损失在总损失的比例,θ表示一个神经网络中的所有参数(一般只有权重w决定)。
常用的R(w)有两种:
第一种:L1正则化

第二种:L2正则化

无论是哪一种正则化方式,基本思想都是希望通过限制权重的大小,使得模型不能任意拟合训练数据中的随机噪音。
L1正则化会让参数变得稀疏(很多参数变为0,可以达到类似特征选取的功能);L2则不会,原因:当参数很小,比如为0.001时,这个参数的平方就可以忽略了,于是模型不会进一步调整参数为0。
L1正则化不可导,L2正则化可导,优化L2更简单。
在实践中,可以将L1和L2同时使用:

带L2正则化的损失函数定义:
import tensorflow as tf
w = tf.Variable(tf.random_normal([2,1],stddev=1,seed=1))
y = tf.matmul(x,w)
loss = tf.reduce_mean(tf.square(y,y_))+tf.contrib.layers.l2_regularizer(lambda)(w)
L1和L2正则化
import tensorflow as tf
weights = tf.constant([[1,-2],[-3,4]],dtype=tf.float32)
with tf.Session() as sess:
print(sess.run(tf.contrib.layers.l1_regularizer(0.5)(weights)))#5
print(sess.run(tf.contrib.layers.l2_regularizer(0.5)(weights)))#7.5
使用集合(collection)
通过集合计算一个5层神经网络带L2正则化损失函数的计算方法:
import tensorflow as tf
#获取一层神经网络上的权重,并将这个权重的l2正则化损失加入"losses"集合
def get_weights(shape,lamda):
#生成一个变量
var = tf.Variable(tf.random_normal(shape),dtype=tf.float32)
#加入集合losses
tf.add_to_collection("losses",tf.contrib.layer.l2_regularizer(lamda)(var))
return var
x = tf.placeholder(tf.float32,shape=(None,2))
y_ = tf.placeholder(tf.float32,shape=(None,1))
batch_size = 8
#每一层网络中的节点数
layer_dimension = [2,10,20,20,1]
n_layers = len(layer_dimension)
cur_layer = x#当前输入层
in_dimension = layer_dimension[0]#当前输出层节点数
#通过循环生成一个5层神经网络
for i in range(1,n_layers):
out_dimension = layer_dimension[i]#下一层节点数
weight = get_weights([in_dimension,out_dimension],0.001)
bias = tf.Variable(tf.constant(0.1,shape=[out_dimension]))
#使用Relu函数
cur_layer = tf.nn.relu(tf.matmul(cur_layer,weight)+bias)
in_dimension = layer_dimension[i]
mse_loss = tf.reduce_mean(tf.square(y_-cur_layer))
tf.add_to_collection("losses",mse_loss)
loss = tf.add_n(tf.get_collection("losses"))
6.滑动平均模型
滑动平均模型,它可以使得模型在测试数据上更健壮,在使用随机梯度下降算法训练神经网络时,通过滑动平均模型可以在很多的应用中在一定程度上提高最终模型在测试数据上的表现。
其实滑动平均模型,主要是通过控制衰减率来控制参数更新前后之间的差距,从而达到减缓参数的变化值(如,参数更新前是5,更新后的值是4,通过滑动平均模型之后,参数的值会在4到5之间),如果参数更新前后的值保持不变,通过滑动平均模型之后,参数的值仍然保持不变。
计算公式:shadow_variable = decay * shadow_variable + (1-decay) * variable
计算公式中的shadow_variable为影子变量,也就是变量在更新之前的值,variable是变量现在的值。decay决定了模型更新的速度,decay越大模型越趋于稳定。
TensorFlow中的ExponentialMovingAverage函数实现了滑动平均模型,下面对该函数进行简单的介绍。
tf.train.ExponentialMovingAverage(decay, num_updates=None, zero_debias=False,name="ExponentialMovingAverage")
参数:
decay:实数类型,衰减率。
num_updates:可选,设置这个参数之后,将会通过min(decay, (1 + num_updates) / (10 + num_updates))函数,从中选择最小值做为衰减率。
返回值:ExponentialMovingAverage对象,通过对象调用apply方法可以通过滑动平均模型来更新参数。
下面用TensorFlow的程序来实现滑动平均模型。
#滑动平均模型
import tensorflow as tf
#定义一个变量用于计算滑动平均,变量的初始值为0,变量的类型必须是实数
v1=tf.Variable(0,dtype=tf.float32)
#定义一个迭代轮数的变量,动态控制衰减率,并设置为不可训练
step=tf.Variable(0,trainable=False)
#定义一个滑动平均类,初始化衰减率为0.99和衰减率的变量step
ema=tf.train.ExponentialMovingAverage(0.99,step)
#定义每次滑动平均所更新的列表
maintain_averages_op=ema.apply([v1])#apply(func [, args [, kwargs ]]) 函数用于当函数参数已经存在于一个元组或字典中时,间接地调用函数。
#args是一个包含将要提供给函数的按位置传递的参数的元组。如果省略了args,任 何参数都不会被传递,kwargs是一个包含关键字参数的字典。
with tf.Session( ) as sess:
#初始化所有变量
init_op=tf.global_variables_initializer()
sess.run(init_op)
#衰减率为min(0.99,(1+step)/(10+step)=0.1}=0.1
print(sess.run([v1,ema.average(v1)]))
#更新v1的滑动平均值
sess.run(tf.assign(v1,5)) #tf.assign(A, new_number): 这个函数的功能主要是把A的值变为new_number
#v1的滑动平均0.1*0+0.9*5=4.5
sess.run(maintain_averages_op)
print(sess.run([v1,ema.average(v1)]))
输出
[0.0, 0.0]
[5.0, 4.5]