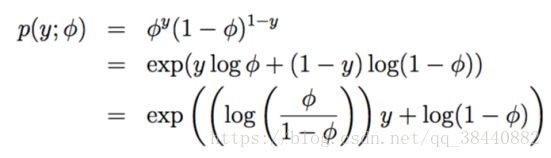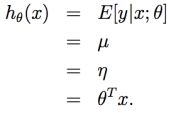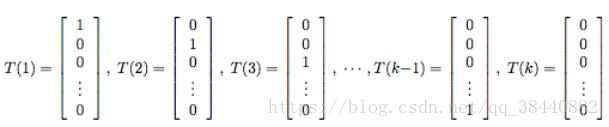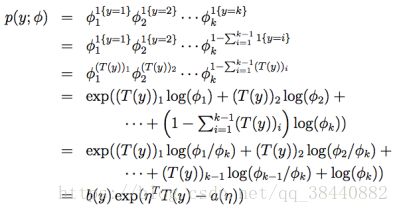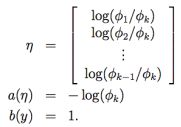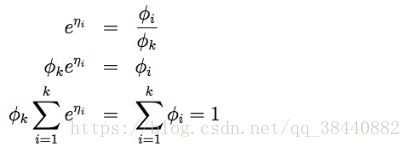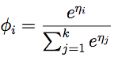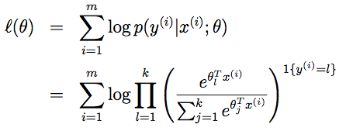machine learning 机器学习入门（四)

构建广义线性模型

先了解一下指数族分布的形式，如果一个分布能用以下的形式写出来，则这个式子为指数族分布

稍微对比思考会发现，之前的分类用的伯努利分布以及高斯分布都是属于指数族分布的

对于伯努利分布，有如下的式子

与指数族的式子相对比会发现，对应关系为

即

其实也就是我们上篇博客说到的logistic函数，从某种层面上也可以解释我们选择logistic函数作为二元分类的概率模型预估。

其他的分布这里就不一一列出来对比了。

设想你要构建一个模型，来估计在给定的某个小时内来到你商店的顾客人数（或者是你的网站的页面访问次数），基于某些确定的特征 x ，例如商店的促销、最近的广告、天气、今天周几啊等等。我们已经知道泊松分布（Poisson distribution）通常能适合用来对访客数目进行建模。知道了这个之后，怎么来建立一个模型来解决咱们这个具体问题呢？非常幸运的是，泊松分布是属于指数分布族的一个分部，所以我们可以使用一个广义线性模型（Generalized Linear Model，缩写为 GLM）。在本节，我们讲一种对刚刚这类问题来构建广义线性模型的方法。 

进一步泛化，设想一个分类或者回归问题，要预测一些随机变量 y 的值，作为 x 的一个函数。要导出适用于这个问题的广义线性模型，就要对我们的模型、给定 x 下 y 的条件分布来做出以下三个假设：

1、y | x; θ ∼ Exponential Family(η)，即给定 x 和 θ, y 的分布属于指数分布族，是一个参数为 η 的指数分布。 


2、给定 x，目的是要预测对应这个给定 x 的 T(y) 的期望值。咱们的例子中绝大部分情况都是 T(y) = y，这也就意味着我们的学习假设 h 输出的预测值 h(x) 要满足 h(x) = E[y|x]。 (注意，这个假设通过对 hθ(x) 的选择而满足，在逻辑回归和线性回归中都是如此。例如在逻辑回归中， hθ (x) = [p (y = 1|x; θ)] =[ 0 · p (y = 0|x; θ)+1·p(y = 1|x;θ)] = E[y|x;θ]。译者注：这里的E[y|x]应该就是对给定x时的y值的期望的意思。)

3、自然参数 η 和输入值 x 是线性相关的，η = θT x，或者如果 η 是有值的向量，则有ηi = θiT x。

上面的几个假设中，第三个可能看上去证明得最差，所以也更适合把这第三个假设看作是一个我们在设计广义线性模型时候的一种 “设计选择 design choice”，而不是一个假设。那么这三个假设/设计，就可以用来推导出一个非常合适的学习算法类别，也就是广义线性模型 GLMs，这个模型有很多特别友好又理想的性质，比如很容易学习。

此外，这类模型对一些关于 y 的分布的不同类型建模来说通常效率都很高；例如，我们下面就将要简单介绍一些逻辑回归以及普通最小二乘法这两者如何作为广义线性模型来推出。（ps:以上这一段直接从课堂笔记中直接复制过来了）

普通最小二乘法

普通最小二乘法其实是广义线性模型的一种特例，假设如下的背景设置：目标变量y（也称响应变量）是连续的，然后我们将x的y分布用高斯分布来建模，其中

μ 可以使依赖 x 的一个函数。这样，我们就让上面的指数分布族的(η)分布成为了一个高斯分布。在前面内容中我们提到过，在把高斯分布写成指数分布族的分布的时候，有μ = η。所以就能得到下面的等式：

第一行的等式是基于假设2；第二个等式是基于定理当 y|x; θ ∼ N (μ, σ2)，则 y 的期望就是 μ；第三个等式是基于假设1，以及之前我们此前将高斯分布写成指数族分布的时候推导出来的性质 μ = η；最后一个等式就是基于假设3。

softmax 回归 

softmax回归其实本质上就是一个多元的分类模型，之前提到的分类问题都是二元（结果为两个种类：eg：是、不是）的，而softamx则是针对多元的分类问题，比如我们设计邮件分类器的时候，不能简单的分为垃圾邮件和非垃圾邮件，在实际生活中往往需要更精细的划分，比如个人私密邮件，工作邮件，垃圾邮件等等，这个时候就不是简单地伯努利分布，而是服从一个多项式分布的实际问题。

要对一个可能有k个输出值的多项式进行参数化，可以用k个参数φ1,...,φk来对应各自输出值的概率，为了表述方便我们可以把第k个φ用前k-1个φ来表示（因为总的和为1），按照下面的方式定义一个 T (y) ∈ ：

 

在介绍一种非常有用的记号。指示函数（indicator function）1{·}，如果参数为真，则等于1；反之则等于0（1{True} = 1, 1{False} = 0）。在此基础上，就有了E[(T(y))i] = P (y = i) = φi。现在一切就绪，可以把多项式写成指数族分布了。

其中有

所以就已经化成了指数族分布的形式

这样咱们就把多项式方程作为一个指数族分布来写了出来。

与 i （for i = 1, ..., k）对应的链接函数为： 

为了方便起见，我们再定义 ηk = log(φk/φk) = 0。对链接函数取反函数然后推导出响应函数，就得到了下面的等式： 

这就说明了φk = 1/ Σki=1 eηi ，然后可以把这个关系代入回到等式(7)，这样就得到了响应函数：

上面这个函数从η 映射到了φ，其实这也就是softmax函数，这个其实和上面伯努利分布推出来的logistic函数一样，所以化为这样可以帮助我们更好地理解某一类问题的内在规律。所以给定x后y的条件分布为

所以可以写出似然函数的对数：

注：这里的y和x都是存在矩阵中。所以得到上面的式子后可以利用梯度上升或者牛顿法求出最大似然来拟合参数。

so cool!