随机森林模型详解

1.定义

决策树+bagging=随机森林，随机森林是一种比较新的机器学习模型(非线性基于树的模型)集成学习方法。上世纪八十年代Breiman等人发明分类树算法，通过反复二分数据进行分类或回归，计算量大大降低，2001年Breiman把分类树组合成随机森林，即在变量(列)的使用和数据(行)的使用上进行随机化，生成很多分类树，再汇总分类树结果。随机森林在运算量没有显著提高前提下提高了预测精度，随机森林对多元共线性不敏感，结果对缺失数据和非平衡数据比较稳健，可以很好地预测多达几千个解释变量的作用，被誉为当前最好算法之一

随机森林是集群分类模型中的一种，随机森林是用随机的方式建立一个森林，森林由很多的决策树组成，且每一棵决策树之间是没有关联的。得到随机森林模型后，当新样本进入时随机森林中的每一棵决策树分别进行判断，bagging集合策略比较简单，对于分类问题通常使用投票法，得到最多票数类别或者类别之一为最终模型输出。对于回归通常使用简单平均法，T个弱学习器得到的回归结果进行算术平均即最终模型输出

随机森林使用CART决策树作为弱学习器

2.优缺点

优点：

a.在数据集上表现良好，两个随机性的引入使随机森林不容易陷入过拟合

b.在当前很多数据集上，相对其他算法有很大优势，两个随机性的引入使得随机森林具有很好的抗噪声能力

c.能处理高维度(feature很多)数据，且不用做特征选择，对数据集适应能力强：既能处理离散型数据，也能处理连续型数据，数据集无需规范化

d.可生成一个Proximities=pij矩阵，用于度量样本间相似性： pij=aij/N, aij表示样本i和j出现在随机森林中同一个叶结点的次数，N随机森林树的颗数

e.创建随机森林时，对generlization error使用的是无偏估计

f.训练速度快，可得到变量重要性排序

g.在训练过程中，能够检测到feature间的互相影响

h.容易做成并行化方法，针对大样本训练速度有优势

i.实现比较简单

缺点：

a.在某些噪音比较大的样本集上，RF模型容易陷入过拟合

b.取值划分比较多的特征容易对RF决策产生更大的影响，从而影响拟合模型效果

3.应用范围

随机森林主要应用于回归和分类。随机森林进行bootstrap抽样，但它与bagging区别是：生成每棵树时每个节点变量都仅在随机选出的少数变量中产生。因此不但样本是随机的，连每个节点变量(Features)的产生都是随机的

许多研究表明组合分类器比单一分类器的分类效果好，随机森林是一种利用多个分类树对数据进行判别与分类的方法，它在对数据进行分类的同时，还可以给出各个变量重要性评分，评估各个变量在分类中所起的作用

4.基本原理

随机森林通过自助法(bootstrap)重采样技术，从原始训练样本集N中有放回地重复随机抽取k个样本(k一般和N相同)生成新的训练样本集，然后根据自助样本集生成n个分类树组成随机森林。其实质是对决策树算法的一种改进，将多个决策树合并在一起，每棵树的建立依赖于一个独立抽取的样本集

特征选择采用随机方法，然后比较不同情况下产生的误差，能检测到内在估计误差、分类能力和相关性决定选择特征的数目。单棵树分类能力可能很小，但在随机产生大量决策树后，一个测试样品可通过每一棵树的分类结果经统计后选择最可能的分类

假设输入的样本量为N个，那么采样样本量也为N个。这样使在训练时每棵树的输入样本都不是全部样本，相对不容易出现over-fitting。然后进行列采样从M个feature中选择m个(m << M)。之后是对采样后的数据使用完全分裂方式建立出决策树，这样决策树某一叶子节点要么是无法继续分裂的，要么里面所有样本都是指向的同一个分类。一般很多决策树算法都一个重要步骤—剪枝，但这里不这样干，由于两个随机采样过程保证了随机性，所以就算不剪枝，也不会出现over-fitting

5.实现过程

随机森林模型的OOB统计，当随机森林模型利用Bootstrap抽样法抽取样本时，以N表示训练集中样本个数，当N足够大时，依据极限推导训练集中每个样本未被抽中的概率为将收敛于36.8%，即原始数据中有接近37%的样本不会出现在Bootstrap样本中，这些数据成为袋外数据，可以用来对模型泛化误差进行估计

1.从原始训练数据集中，应用bootstrap方法有放回地随机抽取k个新自助样本集，并由此构建k棵决策树，每次未被抽到的样本组成Ｋ个袋外数据。2.设有n 个特征，在每一棵树的每个节点处随机抽取mtry 个特征，通过计算每个特征的蕴含信息量，在特征中选择一个最具分类能力的特征进行节点分裂。3.每棵树最大限度生长不做任何剪裁。4.将生成的多棵树组成随机森林，用随机森林对新数据进行分类，分类结果按树分类器投票多少而定

5.1.数据随机选取

首先从原始数据集中采取有放回抽样，构造子数据集，子数据集数据量是与原始数据集相同的，不同子数据集的元素可以重复，同一子数据集中的元素也可重复。第二利用子数据集构建子决策树，将这个数据放到子决策树中，每个子决策树输出一个结果。最后如果有新数据需要通过随机森林得到分类结果，就可通过对子决策树的判断结果投票，得到随机森林输出结果。假设随机森林中有3棵子决策树，2棵子树分类结果是A类，1棵子树分类结果是B类，那么随机森林的分类结果就是A类

5.2.待选特征随机选取

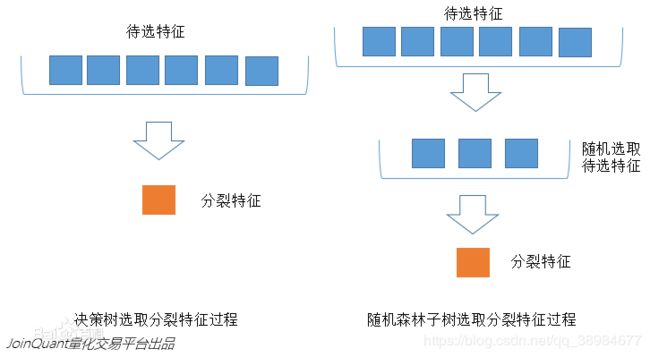
与数据集随机选取类似，随机森林子决策树的每一分裂过程(即每一枝节点处)并未用到所有待选特征，而是从所有待选特征中随机选取一定数量特征(三分之一，值越小模型越健壮，无放回抽取)，之后再在随机选取特征中选取最优特征。这样能使随机森林中的决策树都能彼此不同，提升系统多样性从而提升分类性能

下图蓝色方块代表所有可被选择的特征，也就是目前待选特征。黄色方块是分裂特征。左边是一棵决策树的特征选取过程，通过在待选特征中选取最优分裂特征完成分裂。右边是一颗随机森林子树的特征选取过程

分枝优度准则是基于离均差平方和，假设有p个自变量X=(X1,X2,…,Xp)和连续型因变量Y。对于树某一节点t的样本量为N(t)，可计算该节点的离均差平方和。假定该阶段t内所有可能的分枝集合(含变量和相应切点)为A，分枝s将节点t分裂为两个子节点tl与tr，最佳分枝即使t节点离均差平方和与分裂后两个子节点对应离均差平方和之和差距最大的分枝，即分裂后效果优于分裂前，使得各子节点内的变异最小

将生成的b颗回归树组成随机森林回归模型，回归效果评价采用袋外数据预测均方残差MSE及拟合优度 R2

5.3.重要性评分

定义为袋外数据自变量值发生轻微扰动后的分类正确率与扰动前分类正确率的平均减少量，OOB误差

1.对于每棵决策树，利用袋外数据进行预测，将袋外数据的预测误差记录下来。每棵树误差为：vote1，vote2，...，voteb

2.随机变换每个预测变量，从而形成新的袋外数据，再利用袋外数据进行验证，其每个变量的误差是：vote11，vote12，...，vote1b

3.对于某预测变量，计算其重要性是变换后的预测误差与原来相比差的均值

 6.party包

与randomForest包不同之处在于party可处理缺失值。party包中的随机森林建模函数为cforest(ctree函数建立决策树)，mtry表示在每棵树的每个节点处随机抽取mtry 个特征，通过计算每个特征的蕴含信息量，在特征中选择一个最具分类能力的特征进行节点分裂。varimp代表重要性函数

ctree()不能很好地处理缺失值，含有缺失值的观测有时被划分到左子树，有时划到右子树，这是由缺失值的替代规则决定的

library(party)
set.seed(42)
crf<-cforest(carb~.,control=cforest_unbiased(mtry=2,ntree=50),data=mtcars) 
print(crf)
varimpt<-data.frame(varimp(crf))

 

7.randomForest包

使用randomForest存在两个限制，一是该函数不能处理带有缺失值的数据，要事先对缺失值进行处理。二是分类属性水平划分最大值为32，大于32的分类属性需要事先转换，party包中的cforest没有限定分类属性水平划分数

library(randomForest)
data(iris)
set.seed(100)
ind=sample(2,nrow(iris),replace=TRUE,prob=c(0.8,0.2))

#ntree生成决策树数目
#mtry选择分裂属性个数
#importance=TRUE是否输出分裂属性重要性
#proximity=TRUE表示生成临近矩阵(样本间相似性)
#nperm计算importance重复次数
iris.rf=randomForest(Species~.,iris[ind==1,],ntree=50,nPerm=10,mtry=3,proximity=TRUE,importance=TRUE)
print(iris.rf)
iris.pred=predict(iris.rf,iris[ind==2,])
table(observed=iris[ind==2,"Species"],predicted=iris.pred)

#预测概率即众数的那一类占当前样本集的比例
iris.pred=predict(iris.rf,iris[ind==2,],type="prob");
#type="class"预测分类结果


#重要性绘图函数
varlmpPlot(iris.rf)
#调用plot函数绘制随机森林对象均方差,即绘制误差率
plot(iris.rf)
随机森林默认决策树数目500，分别计算不同数目下误差率
n=500
nerr_train=nerr_test<-rep(0,n)
for(i in 1:n){
	fit<-randomForest(是否流失~.,data=train_data,mtry=6,ntree=i)
	train<-predict(fit,train_data,type="class")
	test<-predict(fit,test_data,type="class")
	nerr_train[i]<-sum(train_data$是否流失!=train)/nrow(train_data)
	nerr_test[i]<-sum(test_data$是否流失!=test)/nrow(test_data)
}
plot(1:n,nerr_train,type="l",ylim=c(min(nerr_train,nerr_test),max(nerr_train,nerr_test)),xlab="数的数目",ylab="误差率",lty=1,col=1)
lines(1:n,nerr_test,lty=2,col=2)
legend("right",lty=1:2,col=1:2,legend =c("训练集","测试集"),bty="n",cex=0.8)

图形给出随机森林ntree取不同数值时，训练集与测试集的误差大小，随着取值不断增大训练集误差在0处稳定，测试集误差波动幅度不断减小，在0.075左右上下波动。可见随机森林对结果的预测并非过拟合