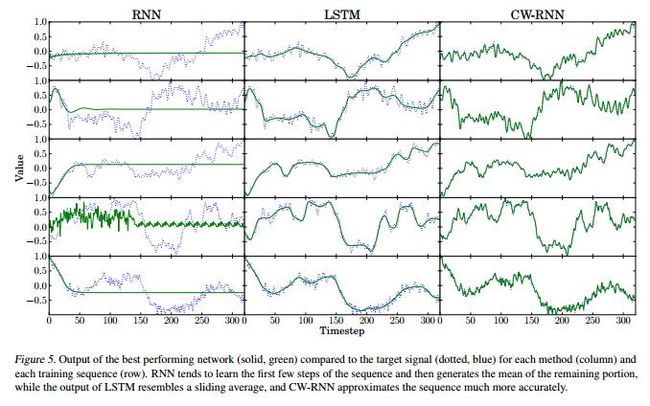
内容来自:A Clockwork RNN
Jan Koutník, Klaus Greff, Faustino Gomez, Jürgen Schmidhuber
CW-RNN是一个带时钟频率的RNN变种,似乎是对回归有不错的效果,不过这个有争论。对一个时间序列,无论是回归还是分类都是将数据经过循环按照时间序列输入,RNN使用隐藏矩阵进行记忆,然后判定输出。针对原始RNN对长序列记忆效果极差,作者在这里设计了一种将隐藏状态矩阵(记忆机制)分割成g个小模块并使用类时钟频率掩码的方式,将RNN的记忆分割成几个部分,然后经过特定设计,使CW-RNN记忆矩阵中每个部分处理不同的时刻的数据,加强记忆效果。
在论文中作者列举的数据显示这种设计在特定的应用中具有更优的效果。例如,对一个长度为L的时间序列进行预测,在使用CW-RNN的时候可以通过设置时钟频率人工设定记忆序列。如,L长度为36,那我们可以设置CW为[1,2,4,8,16,12,18,36],这相当于在长度为36的序列设置了多个记忆点,每个记忆点基于此记忆点之前的输入值进行抽象记忆。这个设计与RNN经典变种LSTM有巨大的差异。LSTM通过gate结构实现自动的记忆选择汲取,这里的CW设计需要有一种类似于先验值的CW设定,这并不是一种十分优雅的设计。但这种设计增加的人工设定序列节点选取的操作空间,应该可以在一定程度上对标收益率的时间序列进行特别设计,从而取得不错的回归效果。
该设计进行时间序列回归拟合,在取局部图的时候可以观察到,LSTM的回归效果相对平滑,而CW-RNN并没有这种缺陷。
import numpy as np
import pandas as pd
# import statsmodels.api as sm
import tensorflow as tf
# import matplotlib.pylab as plt
import seaborn as sns
# %matplotlib inline
sns.set_style('whitegrid')
class ClockworkRNN(object):
def __init__(self,
in_length,
in_width,
out_width,
training_epochs=1e2,
batch_size=1024,
learning_rate=1e-4,
hidden_neurons=360,
Rb=60,
Ti=2,
Ti_sum=6,
display=1e2):
#
self.in_length = in_length
self.in_width = in_width
self.out_width = out_width
self.batch_size = batch_size
self.learning_rate = learning_rate
self.display = display
#
self.hidden_neurons = hidden_neurons
self.Rb = Rb
self.Ti = Ti
self.Ti_sum = Ti_sum
self.clockwork_periods = [self.Ti ** x for x in range(self.Ti_sum)]
self.training_epochs = training_epochs
self.inputs = tf.placeholder(dtype=tf.float32, shape=[None, self.in_length, self.in_width], name='inputs')
self.targets = tf.placeholder(dtype=tf.float32, shape=[None, self.out_width], name='targets')
#
self.__inference()
# 下三角掩码矩阵,处理g-moduels划分形成的上三角权重矩阵
def __Mask_Matrix(self, W, k):
length = np.int(W / k)
tmp = np.ones([W, W])
for i in range(length)[1:]:
tmp[i * k:(i + 1) * k, :i * k] = 0
tmp[(i + 1) * k:, :i * k] = 0
return np.transpose(tmp)
def __inference(self):
self.sess = sess = tf.InteractiveSession()
# 标准RNN初始权重
with tf.variable_scope('input_layers'):
self.WI = tf.get_variable('W', shape=[self.in_width, self.hidden_neurons],
initializer=tf.truncated_normal_initializer(stddev=0.1))
self.bI = tf.get_variable('b', shape=[self.hidden_neurons],
initializer=tf.truncated_normal_initializer(stddev=0.1))
traingular_mask = self.__Mask_Matrix(self.hidden_neurons, self.Rb)
self.traingular_mask = tf.constant(traingular_mask, dtype=tf.float32, name='mask_upper_traingular')
with tf.variable_scope('hidden_layers'):
self.WH = tf.get_variable('W', shape=[self.hidden_neurons, self.hidden_neurons],
initializer=tf.truncated_normal_initializer(stddev=0.1))
self.WH = tf.multiply(self.WH, self.traingular_mask)
self.bH = tf.get_variable('b', shape=[self.hidden_neurons],
initializer=tf.truncated_normal_initializer(stddev=0.1))
with tf.variable_scope('output_layers'):
self.WO = tf.get_variable('W', shape=[self.hidden_neurons, self.out_width],
initializer=tf.truncated_normal_initializer(stddev=0.1))
self.bO = tf.get_variable('b', shape=[self.out_width],
initializer=tf.truncated_normal_initializer(stddev=0.1))
# 输入训练数据转换为列表
X_list = [tf.squeeze(x, axis=[1]) for x
in tf.split(value=self.inputs, axis=1, num_or_size_splits=self.in_length, name='inputs_list')]
with tf.variable_scope('clockwork_rnn') as scope:
# 定义初始时刻的隐藏状态,设定为全0
self.state = tf.get_variable('hidden_sate', shape=[self.batch_size, self.hidden_neurons],
initializer=tf.zeros_initializer(), trainable=False)
for i in range(self.in_length):
# 获取g_moduels索引
if i > 0:
scope.reuse_variables()
g_counter = 0
for j in range(self.Ti_sum):
if i % self.clockwork_periods[j] == 0:
g_counter += 1
if g_counter == self.Ti_sum:
g_counter = self.hidden_neurons
else:
g_counter *= self.Rb
# t时刻eq1
tmp_right = tf.matmul(X_list[i], tf.slice(self.WI, [0, 0], [-1, g_counter]))
tmp_right = tf.nn.bias_add(tmp_right, tf.slice(self.bI, [0], [g_counter]))
self.WH = tf.multiply(self.WH, self.traingular_mask)
tmp_left = tf.matmul(self.state, tf.slice(self.WH, [0, 0], [-1, g_counter]))
tmp_left = tf.nn.bias_add(tmp_left, tf.slice(self.bH, [0], [g_counter]))
tmp_hidden = tf.tanh(tf.add(tmp_left, tmp_right))
# 更新隐藏状态
self.state = tf.concat(axis=1, values=[tmp_hidden, tf.slice(self.state, [0, g_counter], [-1, -1])])
self.final_state = self.state
self.pred = tf.nn.bias_add(tf.matmul(self.final_state, self.WO), self.bO)
# self.cost_sum = tf.reduce_sum(tf.square(self.targets - self.pred))
self.cost = tf.reduce_sum(tf.square(self.targets - self.pred))
self.optimizer = tf.train.AdamOptimizer(self.learning_rate).minimize(self.cost)
self.sess.run(tf.global_variables_initializer())
def fit(self, inputs, targets):
sess = self.sess
for step in range(np.int(self.training_epochs)):
for i in range(np.int(len(targets) / self.batch_size)):
batch_x = inputs[i * self.batch_size:(i + 1) * self.batch_size].reshape(
[self.batch_size, self.in_length, self.in_width])
batch_y = targets[i * self.batch_size:(i + 1) * self.batch_size].reshape(
[self.batch_size, self.out_width])
sess.run(self.optimizer, feed_dict={self.inputs: batch_x, self.targets: batch_y})
if len(targets) % self.batch_size != 0:
batch_x = inputs[-self.batch_size:].reshape([self.batch_size, self.in_length, self.in_width])
batch_y = targets[-self.batch_size:].reshape([self.batch_size, self.out_width])
sess.run(self.optimizer, feed_dict={self.inputs: batch_x, self.targets: batch_y})
if step % self.display == 0:
print(sess.run(self.cost, feed_dict={self.inputs: batch_x, self.targets: batch_y}))
def prediction(self, inputs):
sess = self.sess
tmp = np.zeros(self.out_width)
for i in range(np.int(len(inputs) / self.batch_size)):
batch_x = inputs[i * self.batch_size:(i + 1) * self.batch_size].reshape(
[self.batch_size, self.in_length, self.in_width])
tmp = np.vstack((tmp, sess.run(self.pred, feed_dict={self.inputs: batch_x})))
if len(inputs) % self.batch_size != 0:
batch_x = inputs[-self.batch_size:].reshape([self.batch_size, self.in_length, self.in_width])
tp = np.vstack((tmp, sess.run(self.pred, feed_dict={self.inputs: batch_x})))
l = len(targets) % self.batch_size
tp = tp[-l:]
tmp = np.vstack((tmp, tp))
tmp = np.delete(tmp, 0, 0)
return tmp
tmp = pd.read_csv('SHCOMP.csv')
tmp['trading_moment'] = pd.to_datetime(tmp['DATE'].values)
tmp.set_index('trading_moment', drop=True, inplace=True)
tmp['Returns'] = np.log(tmp.Close.shift(-10) / tmp.Close)
tmp.dropna(inplace=True)
tp = np.array(tmp['Returns'])
# del tmp['Unnamed: 0']
in_length = 36
out_length = 1
inputs = np.zeros(in_length)
targets = np.zeros(1)
for i in range(len(tp))[in_length:-out_length]:
m = tp[i - in_length:i]
R = tp[i:i + 1]
inputs = np.vstack((inputs, m))
targets = np.vstack((targets, R))
targets = np.delete(targets, 0, 0)
inputs = np.delete(inputs, 0, 0)
T_inputs = inputs[:512]
T_targets = targets[:512]
a = ClockworkRNN(36, 1, 1, training_epochs=2e4, batch_size=512)
a.fit(T_inputs, T_targets)
outputs = a.prediction(T_inputs)
CW_RNN = outputs
show = pd.DataFrame([T_targets.ravel('C'), outputs.ravel('C')]).T
show.plot()