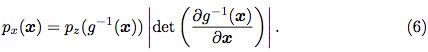2 生成式模型如何工作?比较 GANs 和其他生成式模型有何不同?
我们现在了解了生成式模型能做什么以及为何有必要来构建生成式模型。现在我们要问:生成式模型如何工作的?尤其是,相比于其他的生成式模型,GANs 如何工作?
2.1 最大似然估计(Maximum likelihood estimation)
为了简化讨论,我们先来看看通过最大似然原理进行的生成式模型。不是所有的生成式模型采用最大似然。一些生成式模型默认是不使用最大似然的,但是可以通过改动来使用(GANs 就落在这类)。如果忽略那些不使用最大释然,聚焦于一般不用最大似然的模型的最大似然版本的模型,我们可以去掉不同模型之间的一些让人格外分心的差异。
最大似然的基本想法是定义一个给出参数为 θ 的概率分布的估计的模型。然后将 似然(likelihood) 定义为模型分配给训练数据的概率
这个数据集包含 m 个样本 x (i)。
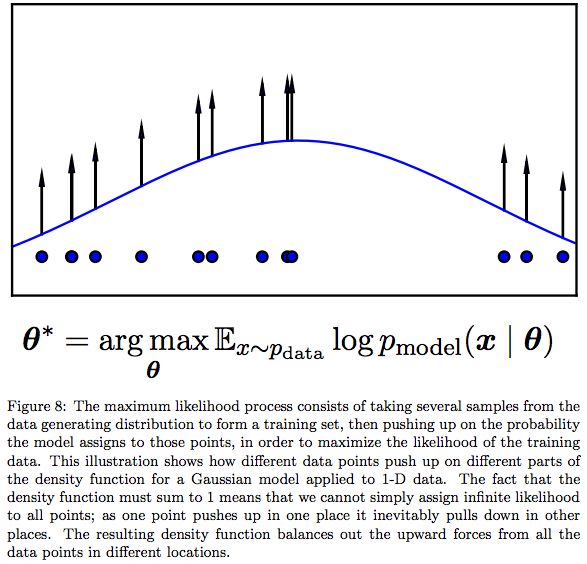
最大似然的原理实际上就是选择可以最大化训练数据的似然的模型参数。这在对数空间中很容易完成,我们可以将原来的乘积转化为求和。这样可以简化似然关于模型的导数的代数表达式,而且在用计算机实现的时候,也能够避免数值问题,比如说乘上几个很小的概率值的时候出现的下溢情形。
在(2)式中,我们用到了性质:对正数 v,有
由于对数函数是一个单调增函数,并不会概率最大值的位置。
在图 8 中我们给出最大似然过程的示例。
我们同样可以将最大似然估计看做是最小化生成概率分布和模型的 KL散度:
如果我们能够足够准确地做到此操作,那么若 pdata 处在分布 pmodel(x;θ) 族中,则模型能够准确地恢复 pdata。实践中,我们不能获取 pdata 本身,而仅仅是从pdata中采样出的 m 个样本的训练集。我们使用这些来定义 p^data,即将概率放在这 m 个点上的经验分布,来近似pdata。最小化 p^data 和 pmodel 之间的 KL 散度实际上就和最大化训练集的似然完全等价。
对最大似然和其他统计估计量更加详细的讨论参见 Goodfellow 等人深度学习书中第 5 章。
2.2 深度生成式模型的分类
如果我们将注意力放在通过最大化似然的深度生成式模型上,我们可以通过对比他们计算似然及其梯度或者近似这些量的方式来比较这几种模型。如前面提到的,这些模型中很多是不通过最大似然的原理进行的,但是我们可以检查这些模型的最大似然变体来减少这些方法之间的不同。所以按照这样的观点,我们构建了在图 9 中的分类。分类树的每个叶子都有其优缺点。GANs 为了避免这样缺点设计而成,但同时也引入一些新的缺点。
2.3 显式的密度模型
在分类树的左边分支是定义了显式的密度函数 pmodel(x;θ)。对这些模型,最大化似然是直接的;我们简单地将模型定义密度函数插入到似然函数的表达式中,然后使用梯度上升即可。
显式的密度模型引入的主要困难是设计一个可以刻画要被生成的数据所有复杂性的模型同时又能保持计算易解性。有两种不同的解决策略来解决这个问题:(1)精心设计模型来保证易解性,在 2.3.1 节会进行解释,(2)模型可以获得似然及其梯度的易解近似,在 2.3.2 节解释。
2.3.1 易解显式模型
在分类树最左的叶子上面的模型定义了一个显式的计算易解的密度函数。目前有两种方法来解决:全可见信念网络(Fully visible belief networks)和非线性独立成分分析(Non linear independent components analysis)。
全可见信念网络 全可见信念网络(Frey et al. 1996; Frey, 1998) 或者 FVBN 是使用概率链式法则将一个 n-维向量 x 分解为一维概率分布的乘积形式的概率分布:
FVBNs 是生成式建模的三个流行方法之一,另外两个是 GANs 和变分自编码器。他们形成了来自 DeepMind 复杂生成式模型(如 Wavenet,Oord et al., 2016)的基础。Wavenet 能够产生真实的人类语音。FVBNs 的主要缺点是样本必须每次产生一个:首先是 x1,然后是 x2
等等,所以生成一个样本的代价是 O(n)。在现代 FVBN 如 Wavenet 中,在每个 xi 上的分布用一个深度神经网络计算得出,所有这 n 个步骤需要特别大的计算量。而且,这些步骤不能并行。Wavenet 需要两分钟才能产生一秒的声音,不能进行交互式对话。GANs 设计为能够并行产生所有的 x,有着更好的生成速度。
非线性独立成分分析 另一类有着显式密度函数的深度生成式模型族是基于两个不同空间的连续、非线性变化的。例如,如果有一个隐含变量 z 向量和一个连续、可微分、可逆的变换 g 使得 g(z) 得到一个在 x 空间的模型产生的样本,那么
�所以 px 易解当密度 pz 易解且g-1 Jacobian 行列式易解。换言之,在 z 上的简单的分布加上一个变换 g 可以用复杂方式来对空间进行变形可以产生一个 x 上的复杂分布,如果 g 设计得很巧妙,这个密度也会易解。使用非线性 g 函数的模型最早可以追溯到 Deco 和 Brauer(1995) 的工作。而这个族的最新成员是 real NVP(Dinh et al., 2016)。参见图 10中由 real NVP 生成的 ImageNet 样本。非线性 ICA 模型主要缺点是他们引入对函数 g 的限制。特别是,可逆性要求意味着隐含变量 z 必须有和 x 同样的维度。GANs 的设计思想就是减少这样的对 g 的限制,尤其是可以使用比 x 更大维度的 z。
如果想了解更多的关于用来定义 FVBN 的概率链式法则或者用来定义非线性 ICA 模型的概率密度函数的确定型变换的影响,请参考 Goodfellow et al. 书的第 3 章。
这里总结一下,定义了一个显式、易解密度函数的模型是非常有效的,因为他们可以直接在训练数据的对数似然上直接应用优化算法。然而,拥有易解密度的模型族其实很有限,不同的族也有相应不同的缺点。
2.3.2 需要近似的显式模型
为了避开由设计易解密度函数的要求带来的缺点,另外也有一些模型可以有显式的密度函数,这些函数是不易解的,需要使用近似来最大化似然。这些基本上被分为两个类别:使用确定型近似(一般就是指变分方法)和随机近似方法(Markov chain Monte Carlo,MCMC 方法)。
变分近似 变分方法定义了一个下界
最大化 L 的学习算法确保能够获得至少和其作用在 L 上一样高的似然值。对许多模型的族,即使在对数似然不是易解的情形下,可以定义一个 L 是计算易解的。目前,在深度生成式模型中变分学习最流行的方法就是 变分自编码器(Variational autoencoder)(Kingma, 2013;Rezende et al., 2014) 或者 简称 VAE。变分自编码器是最流行的三个深度生成式模型之一,除此之外就是 FVBNs 和 GANs。而变分方法的主要缺点就是,当近似后验分布太弱或者先验分布太弱,即使有一个完美的优化算法和无限的训练数据,L 和真实的似然之间的间隔会导致 pmodel 学到和真实的 pdata 不同的东西。GANs 被设计成无偏的,就是说在给定足够大的模型和无限数据的情况下,GAN 博弈的 Nash 均衡能够准确恢复 pdata。在实践中,变分方法通常能够获得非常好的似然,但是会产生低质量的样本。并没有一种好的方法来量化样本的质量,所以这其实是一个主观判断,不是实验事实。参见图 11 VAE 生成的样本。尽管很难指出 GAN 设计的一个方面说这是获得更好样本的起作用的部分,GANs 一般会生成更好的样本。对比 FVBNs,VAEs 是更难优化的,但是 GANs 并不是在这个方面做了优化,参考 Goodfellow 书的第 19 章。
实验中,高度灵活的先验或者灵活的近似后验的 VAEs 可以获得靠近他们自身对数似然 L 的值(Kingma et al., 2016; Chen et al., 2016)当然,这是测试目标和最大界的界之间的间隔。VAEs 能够得到与其他方面相差不多的似然,也就是说他们同样靠近目标的最大值。L. Dinh 和 D. Kingma 已经给出了一个猜想,模型族(Dinh et al., 2014; Rezende and
Mohamed, 2015; Kingma et al., 2016; Dinh et al., 2016) 可以用作 VAE 先验或者近似后验是通用近似子。如果这个被证明,就可以知道 VAEs 是渐进一致的。
Markov chain 近似 大多数深度学习算法使用某种形式的随机近似,至少是采用了使用小量随机选择的训练样本形成一个小批量来最小化期望损失函数。通常,基于采样的近似在有用的样本被快速采样(比如说,选择单个样本操作代价很小)并且只要这些样本方差也不高的情形下能够表现的很好。一些模型需要采取 Markov chain 来生成更加昂贵的样本。Markov chain 是一个通过重复采样样本 x'~q(x'|x) 来生成样本的过程。并根据变换算子 q来更新 x,Markov chain 方法可以保证 x 最终会收敛到一个来自 pmodel(x) 的样本。不幸的是,这个收敛过程会非常缓慢,也没有很好的方法来测试是否已经收敛,所以在实践中,通常会在其没有真正收敛到一个 pmodel 的样本时,过早使用 x。在高维空间中,Markov chain 更加低效。Botlzmann machiness (Fahlman et al., 1983; Ackley et al., 1985; Hinton et al., 1984; Hinton and
Sejnowski, 1986) 是依赖于 Markov chain 训练模型和生成样本的一类生成式模型。Botlzmann machines 在深度学习复兴的开始发挥了重要作用(Hinton et al., 2006; Hinton, 2007) 但是现在很少有人使用了,最大的原因是其依赖的 Markov chain 近似技术在 ImageNet 这样的问题上难以规模化。而且,即使 Markov chain 方法能够规模化很好用来训练,用其进行样本生成也有非常大的计算消耗,大家往往会选择单步生成方法。也是因为这样的原因,GANs 才设计成避免使用 Markov chain。对 Markov chain Monte Carlo 近似更详细的讨论参见 Goodfellow 书的第 18 章。在同一本书的第 20 章有对 Botlzmann machines 的介绍。
还有一些方法同时使用了变分和 Markov chain 近似。例如,深度 Boltzmann machine 用了这两个类型的近似(Salakhutdinov and Hinton, 2009).
2.4 隐式密度模型
有些模型可以不需要显式定义一个密度函数进行训练。这些模型给出了一种间接和pmodel 进行交互的方式(通常是从中进行采样)训练模型。这些技术构成了图 9 中分类图的第二个分支。
一些基于从pmodel 进行采样的方式隐式模型定义了一个 Markov chain 转移算子,必须运行多次来从模型中获得一个样本。这个家族中的首个例子就是生成式随机网络(Generative stochastic network)(Bengio et al., 2014)。正如 2.3.2 节中讲的那样,Markov chain 常常不能规模化到高维空间中,而且在生成时也有过高的计算代价。GANs 就是针对这些问题进行设计的。
最后,最右边的叶子是单步生成样本的隐式模型族。在这个家族中,GANs 是唯一一个成员,但是后来也有了 Kernelized moment matching 这样的模型(Li et al., 2015; Dziugaite et al., 2015).
2.5 对比 GANs 和其他生成式模型
总结一下,GANs 针对其他生成式模型的缺点进行设计的:
- 他们可以并行生成样本,而不是随 x 的维度变化的运行时间。这是相对于 FVBN 的优点。
- 生成器函数的设计只有很少的限制。这个优点是对比于 Boltzmann machine 说的,因为很少概率分布能够给出易解的 Markov chain 采样,而相比较于非线性 ICA,则因为生成器必须是可逆的而且隐含编码 z 必须要和样本 x 有着同样的维度。
- 不需要 Markov chain。这相较于 Boltzman machines 和 GSNs
- 不需要有变分界,在 GANs 框架中可用的特定模型族已经证实是通用近似子,所以 GANs 其实是渐进一致的。某些 VAEs 被猜想是渐进一致的,但还没有被证实。
- 主观上判断 GANs 能够产生比其他方法更好的样本。
同时,GANs 也有新的缺点,训练 GANs 需要找到博弈的 Nash 均衡,这个其实是一个比优化目标函数更加困难的问题。