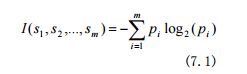“什么是判定树?”判定树是一个类似于流程图的树结构;其中,每个内部结点表示在一个属性上的测试,每个分枝代表一个测试输出,而每个树叶结点代表类或类分布。树的最顶层结点是根结点。一棵典型的判定树如图 7.2 所示。它表示概念 buys_computer,即,它预测 AllElectronics的顾客是否可能购买计算机。内部结点用矩形表示,而树叶用椭圆表示。
为了对未知的样本分类,样本的属性值在判定树上测试。路径由根到存放该样本预测的叶结点。判定树容易转换成分类规则。
在 7.3.1 小节, 我们介绍学习判定树的基本算法。在判定树构造时,许多分枝可能反映的是训练数据中的噪音或局外者。树剪枝试图检测和剪去这种分枝,以提高在未知数据上分类的准确性。树剪枝在 7.3.2 小节介绍。由判定树提取分类规则在 7.3.3 小节讨论。基本判定树算法的加强在7.3.4 小节给出。大型数据库判定树归纳的可规模性问题在 7.3.5 小节讨论。7.3.6 小节介绍判定树归纳与诸如数据方等数据仓库机制的集成,允许多个粒度层的判定树挖掘。判定树已在由医疗到游戏理论和商务等应用领域广泛使用。判定树是一些商业规则归纳系统的基础。
算法:Generate_decision_tree。由给定的训练数据产生一棵判定树。
输入:训练样本 samples,由离散值属性表示;候选属性的集合 attribute_list。
输出:一棵判定树。
方法:由训练样本归纳判定树的基本算法
(1) 创建结点 N;
(2) if samples 都在同一个类 C then
(3) return N 作为叶结点,以类 C 标记;
(4) if attribut_list 为空 then
(5) return N 作为叶结点,标记为 samples 中最普通的类; //majority voting
(6) 选择 attribute_list 中具有最高信息增益的属性 test_attribute;
(7) 标记结点 N 为 test_attribute;
(8) for each test_attribute 中的未知值 a i //partition the samples
(9) 由结点 N 长出一个条件为 test_attribute = a i的分枝;
(10) 设 si 是 samples 中 test_attribute = a i的样本的集合;//a partition
(11) if si 为空 then
(12) 加上一个树叶,标记为 samples 中最普通的类;
(13) else 加 上 一 个 由 Generate_decision_tree(si,attribute_list–test_attribute)返回的结点;
7.3.1 判定树归纳
判定树归纳的基本算法是贪心算法,它以自顶向下递归的划分-控制方式构造判定树。由训练样本归纳判定树的基本算法是一种著名的判定树算法 ID3 版本。算法的扩展将在 7.3.2 到 7.3.6 小节讨论。算法的基本策略如下:
i) 树以代表训练样本的单个结点开始(步骤 1)。
ii) 如果样本都在同一个类,则该结点成为树叶,并用该类标号(步骤 2 和 3)。
iii) 否则,算法使用称为信息增益的基于熵的度量作为启发信息,选择能够最好地将样本分类的属性(步骤 6)。该属性成为该结点的“测试”或“判定”属性(步骤 7)。在算法的该版本中,所有的属性都是分类的,即离散值。连续属性必须离散化。
iv) 对测试属性的每个已知的值,创建一个分枝,并据此划分样本(步骤 8-10)。
v) 算法使用同样的过程,递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上,就不必该结点的任何后代上考虑它(步骤 13)。
vi) 递归划分步骤仅当下列条件之一成立停止:
(a) 给定结点的所有样本属于同一类(步骤 2 和 3)。
(b) 没有剩余属性可以用来进一步划分样本(步骤 4)。在此情况下,使用多数表决(步骤 5)。这涉及将给定的结点转换成树叶,并用样本中的多数所在的类标它。替换地,可以存放结点样本的类分布。
(c) 分枝 test_attribute = a i没有样本(步骤 11)。在这种情况下,以 samples 中的多数类创建一个树叶(步骤 12)。
属性选择度量
在树的每个结点上使用信息增益度量选择测试属性。这种度量称作属性选择度量或分裂的优劣度量。选择具有最高信息增益(或最大熵压缩)的属性作为当前结点的测试属性。该属性使得对结果划分中的样本分类所需的信息量最小,并反映划分的最小随机性或 “不纯性”。这种信息理论方法使得对一个对象分类所需的期望测试数目最小,并确保找到一棵简单的(但不必是最简单的)树。
设 S 是 s 个数据样本的集合。假定类标号属性具有 m 个不同值,定义 m 个不同类 Ci (i = 1,...,m)。设 si是类 Ci中的样本数。对一个给定的样本分类所需的期望信息由下式给出:
其中,pi是任意样本属于 Ci的概率,并用 si /s 估计。注意,对数函数以 2 为底,因为信息用二进位编码。设属性 A 具有 v 个不同值{a1 ,..., av}。可以用属性 A 将 S 划分为 v 个子集{S1 ,..., Sv};其中,Sj包含 S 中这样一些样本,它们在 A 上具有值 aj。如果 A 选作测试属性(即,最好的划分属性),则这些子集对应于由包含集合 S 的结点生长出来的分枝。设 sij是子集 Sj中类 Ci的样本数。根据 A划分子集的熵或期望信息由下式给出:
换言之,Gain(A)是由于知道属性 A 的值而导致的熵的期望压缩。
算法计算每个属性的信息增益。具有最高信息增益的属性选作给定集合 S 的测试属性。创建一个结点,并以该属性标记,对属性的每个值创建分枝,并据此划分样本。
例 7.2 判定树归纳。
表 7.1 给出了取自 AllElectronics 顾客数据库数据元组训练集。(该数据取自[Qui86])。类标号属性 buys_computer 有两个不同值(即, {yes, no}),因此有两个不同的类(m = 2)。设类 C1对应于 yes,而类 C2对应于 no。类 yes 有 9 个样本,类 no 有 5 个样本。为计算每个属性的信息增益,我们首先使用(7.1)式,计算对给定样本分类所需的期望信息:
下一步,我们需要计算每个属性的熵。让我们从属性 age 开始。我们需要观察 age 的每个样本值的 yes 和 no 分布。我们对每个分布计算期望信息。
总而言之,判定树归纳算法已在广泛的应用领域用于分类。这种系统不使用领域知识。判定树归纳的学习和分类步骤通常很快。
7.3.2 树剪枝
当判定树创建时,由于数据中的噪音和局外者,许多分枝反映的是训练数据中的异常。剪枝方法处理这种过分适应数据问题。通常,这种方法使用统计度量,剪去最不可靠的分枝,这将导致较快的分类,提高树独立于测试数据正确分类的可靠性。
“树剪枝如何做?”有两种常用的剪枝方法。
在先剪枝方法中,通过提前停止树的构造(例如,通过决定在给定的结点上不再分裂或划分训练样本的子集)而对树“剪枝”。一旦停止,结点成为树叶。该树叶可能持有子集样本中最频繁的类,或这些样本的概率分布。在构造树时,统计意义下的度量,如χ2、信息增益等,可以用于评估分裂的优劣。如果在一个结点划分样本将导致低于预定义阈值的分裂,则给定子集的进一步划分将停止。然而,选取一个适当的阈值是困难的。较高的阈值可能导致过分简化的树,而较低的阈值可能使得树的化简太少。
第二种方法是后剪枝方法,它由“完全生长”的树剪去分枝。通过删除结点的分枝,剪掉树结点。代价复杂性剪枝算法是后剪枝方法的一个实例。最下面的未被剪枝的结点成为树叶,并用它先前分枝中最频繁的类标记。对于树中每个非树叶结点,算法计算该结点上的子树被剪枝可能出现的期望错误率。然后,使用每个分枝的错误率,结合沿每个分枝观察的权重评估,计算不对该结点剪枝的期望错误率。如果剪去该结点导致较高的期望错误率,则保留该子树;否则剪去该子树。逐渐产生一组被剪枝的树之后,使用一个独立的测试集评估每棵树的准确率,就能得到具有最小期望错误率的判定树。
我们可以根据编码所需的二进位位数,而不是根据期望错误率,对树进行剪枝。“最佳剪枝树”使得编码所需的二进位最少。这种方法采用最小描述长度(MDL)原则。由该原则,最简单的解是最期望的。不象代价复杂性剪枝,它不需要独立的样本集。
也可以交叉使用先剪枝和后剪枝,形成组合式方法。后剪枝所需的计算比先剪枝多,但通常产生更可靠的树。
7.3.3 由判定树提取分类规则
“我可以由我的判定树得到分类规则吗?如果能,怎么做?”可以提取判定树表示的知识,并以 IF-THEN 形式的分类规则表示。对从根到树叶的每条路经创建一个规则。沿着给定路经上的每个属性-值对形成规则前件(“IF”部分)的一个合取项。叶结点包含类预测,形成规则后件(“THEN”部分)。IF-THEN 规则易于理解,特别是当给定的树很大时。
例 7.3 由判定树产生分类规则。
沿着由根结点到树叶结点的路经,图 7.2 的判定树可以转换成 IF-THEN 分类规则。由图 7.2 提取的规则是:
IF age = ”<=30” AND student = “no” THEN buys_computer = “no”
IF age = ”<=30” AND student = “yes” THEN buys_computer = “yes”
IF age = ”31...40” THEN buys_computer = “yes”
IF age = ”>40” AND credit_rating =“excellent” THEN buys_computer = “no”
IF age = ”>40” AND credit_rating =“fair” THEN buys_computer = “yes”
C4.5(ID3 算法的后继版本)使用训练样本估计每个规则的准确率。由于这将导致对规则的准确率的乐观估计,C4.5 使用一种悲观估计来补偿偏差。替换地,也可以使用一组独立于训练样本的测试样本来评估准确性。通过删除规则前件中无助于改进规则评估准确性的条件,可以对规则“剪枝”。对于每一类,类中规则可以按它们的精确度定序。由于一个给定的样本可能不满足任何规则前件,通常将一个指定主要类的省缺规则添加到规则集中。
7.3.4 基本判定树归纳的加强
“对基本判定树归纳的加强有哪些?”业已提出了许多对 7.3.1 小节判定树归纳基本算法的加强。本小节,我们将讨论若干主要加强,其中一些结合到 ID3 的后继算法 C4.5 中。
7.3.1 小节的判定树归纳基本算法要求所有的属性是分类的或离散化的。可以修改该算法,允许属性具有整个离散区间或连续值。在这种属性 A 上的测试导致两个分枝,对应于条件 A ≤ V 和 A >V,其中 V 是 A 的某个数值值。给定 A 的值 v,确定 V 时考虑 v-1 个可能的分割。通常,考虑每对相邻值的中间值。如果这些值已预先排序,则只需要扫描一次这些值。信息增益度量有倾斜,它倾向于适合具有许多值的属性。已经提出了一些替代的方法,如增益率,它考虑每个属性值的概率。还有一些其它选择度量,包括 Gini 索引,χ2相依表统计和 G-统计。已经提出了许多方法来处理遗漏的属性值。例如,属性 A 的遗漏值或未知值可以用 A 的最常见值替代。替换地,属性 A 的外观上的信息增益也可以根据 A 的值未知的样本百分比减少。这样,具有缺少值的样本“片段”可以在测试结点被划分到多个分枝。其它方法可能寻找 A 的最可能值,或使用 A 和其它属性的已知联系。
通过重复地将数据划分成越来越小的部分,判定树归纳可能面临碎片、重复和复制问题。碎片是指一个给定分枝中的样本数太小,没有统计意义。解决该问题的一种方法是将分类属性值分组。树结点可以测试一个属性值是否属于给定的集合,如 Ai∈{a1, a2, ..., an}。另一种替代是创建二叉判定树,其每个分枝拥有一个属性上的布尔测试。二叉树导致较少的数据碎片。一些实验研究发现二叉判定树比传统的判定树更精确。当一个属性沿树的一个给定分枝重复测试时,就出现重复。复制是复制树中已存在的子树。属性(特征)构造是防止这三个问题的一种方法。通过由给定的属性创建新的属性,改进给定属性的受限表示。属性构造作为数据变换的一种形式,已在第 2 章讨论过。
业已提出了判定树归纳的增量版本。当给定新的训练数据时,增量方法重新构造由先前的训练数据学习获得的判定树,而不是“盲目地”通过学习构造一棵新树。
还有一些对基本判定树归纳的加强,它们关注可规模性和与数据仓库技术的集成。这些分别在7.3.5 和 7.3.6 小节讨论。
7.3.5 判定树归纳的可规模性
“判定树归纳的可规模性如何?”已有的判定树算法,如 ID3 和 C4.5,对于相对小的数据集是很有效的。当这些算法用于非常大的、现实世界数据库的挖掘时,有效性和可规模性就成了关注的问题。大部分判定树算法都限制训练样本驻留主存。在数据挖掘应用中,包含数以百万计样本的非常大的训练集是很普通的。因此,这一限制就制约了这些算法的可规模性。由于训练样本在主存和高速缓存换进换出,判定树的构造可能变得效率低下。由大型数据库构造判定树的早期策略包括对连续属性离散化,在每个结点对数据选样。然而,这些仍然假定训练集可以放在主存。一种替代的方法是:首先,将样本划分成子集,使得每个子集可以放在内存;然后,由每个子集构造一棵判定树;最后,输出的分类法将由每个子集得到的分类法组合在一起。尽管该方法可以用于大数据集的分类,其分类的准确性不如一次使用所有的数据的方法高。
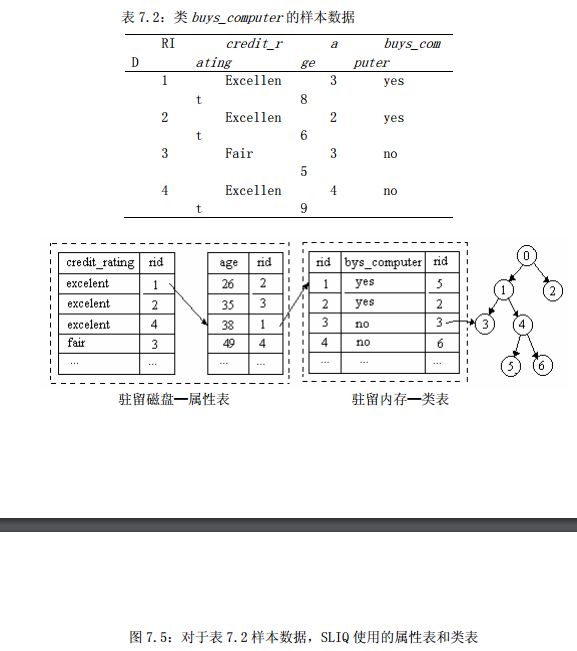
最近,已经提出了一些判定树算法,它们强调可规模性。由非常大的训练集进行判定树归纳的算法包括 SLIQ 和 SPRINT;它们都能处理分类属性和连续值属性。这两种算法都使用了预排序技术,对非常大,而不能放入内存的驻留磁盘的数据集进行预排序。两种算法都定义使用新的数据结构,以利于树的构造。SLIQ 使用若干驻留磁盘的属性表和单个驻留主存的类表。对于表 7.2 的样本数据,SLIQ 产生的属性表和类表如图 7.5 所示。每一个属性具有一个属性表,在 RID(记录标识)建立索引。每个元组由一个从每个属性表的一个表目到类表的一个表目(存放给定元组的类标号)的链接表示。而类表表目链接到它在判定树中对应的叶子结点。类表驻留在主存,因为判定树的构造和剪枝时,经常访问它。类表的大小随训练集中元组数目成比例增长。当类表不能放在主存时,SLIQ 的性能下降。
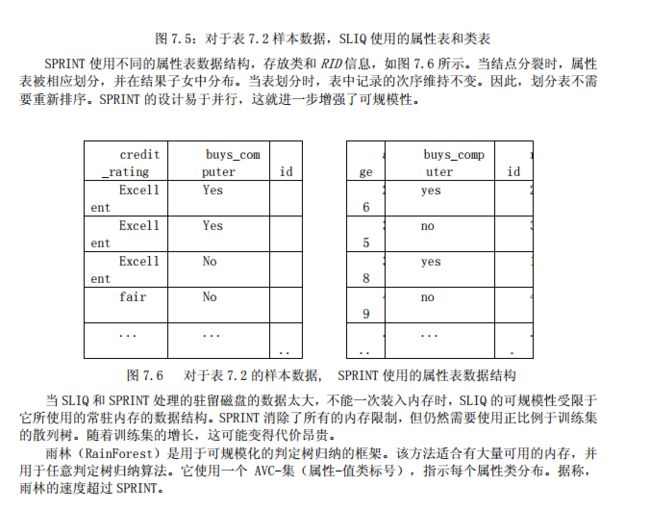
SPRINT 使用不同的属性表数据结构,存放类和 RID 信息,如图 7.6 所示。当结点分裂时,属性表被相应划分,并在结果子女中分布。当表划分时,表中记录的次序维持不变。因此,划分表不需要重新排序。SPRINT 的设计易于并行,这就进一步增强了可规模性。
7.3.6 集成数据仓库技术和判定树归纳
判定树归纳可以与数据仓库技术集成,用于数据挖掘。本小节,我们讨论多维数据方方法和面向属性的归纳如何与判定树归纳集成,以利于交互的多层挖掘。一般地,这里介绍的技术也可以用于其它形式的学习。
数据方方法可以与判定树归纳集成,提供交互的判定树的多层挖掘。数据方和存放在概念分层中的知识可以用于在不同的抽象层归纳判定树。此外,一旦导出判定树,概念分层可以用来泛化或特化树的结点,可以在属性上进行上卷或下钻,并对新的特定抽象层的数据重新分类。这种交互特点使得用户可以将他们的注意力集中在他们感兴趣的树区域或数据。
面向属性的归纳(AOI)使用概念分层,通过以高层概念替换低层概念泛化训练数据(第 5 章)。当我们将 AOI 与判定树归纳集成时,泛化到很低的(特定的)概念层可能导致非常大而茂盛的树。对非常高的概念层的泛化可能导致判定树没什么用;这里,由于过度泛化,一些有趣、重要的子概念丢失了。应当泛化到由领域专家设定,或由用户指定的阈值控制的某个中间概念层。这样,AOI的使用可能产生更易理解的、较小的分类树,从而得到的树比直接在低层、非泛化的数据集上操作的方法(如 SLIQ 或 SPRINT)产生的树更易于解释。
对判定树的典型批评是,由于递归地划分,一些数据子集可能变得太小,使得进一步划分它们就失去统计意义。这种“无意义”的数据子集的最大尺寸可以统计地确定。为处理这一问题,可以引进一个例外阈值。如果给定子集中的样本数少于该阈值,该子集的进一步划分停止。替换地,创建一个叶结点,存放该子集和该子集样本的类分布。
由于大型数据库中的数据量大、发散,假定每个树叶包含属于一个公共类的样本可能是不合理的。这一问题可以通过使用准确率或分类阈值解决。如果属于给定结点的任意类的样本百分比超过该阈值,在给定结点上的进一步划分将终止。
数据挖掘查询语言可以容易地用于说明增强的判定树归纳方法。假定数据挖掘任务是根据顾客的收入和职业,预测 30 多岁的顾客的信用风险,可以用如下数据挖掘查询来说明:
mine classfication
analyze credit_risk
in relevance to income,occupation
from Customer_db
where (age>=30) and (age<40)
display as rules
上面用 DMQL 表达的查询在 Customer_db 上执行关系查询,提取任务相关的数据。不满足 where子句条件的元组将被忽略,并且仅收集 in relevance to 子句中说明的属性和类标号属性(credit_risk)。然后,AOI 在这些数据上操作。由于该查询并未说明所用的概念分层,因此使用省缺的概念分层。可以设计一个图形用户界面,使得用户通过这种数据挖掘查询语言说明数据挖掘任务更加容易。借助于这种办法,用户可以指导自动的数据挖掘过程。