线性模型形式简单、易于建模,但却蕴含着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型都可在线性模型的基础上引入层级结构或高维映射得到。
基本形式
给定由d个属性描述的示例x=(x1; x2;...;xd),其中xi是x是第i个属性上的取值,线性模型试图学得一个通过属性的线性组合来进行预测的函数,即f(x)=w1x1+w2x2+...wdxd+b,一般用向量形式写成f(x)=wTx+b,w和b学得之后模型就得以确定
线性回归
下面我们用一个预测房价的例子来说明。
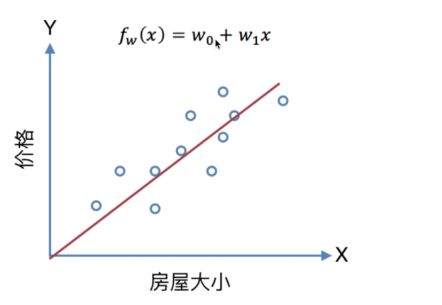
选择合适模型
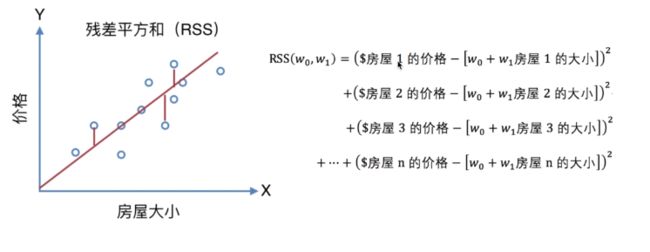
横轴为房屋大学,纵轴为房屋出售的价格。由上述可知,w1和w0是需要学得的参数。不同的参数会拟合成不同的直线。我们需要的是一条成本最小的直线,通常用RSS残差平方和来表示。
那如果我们用更高阶的函数来拟合这个数据呢?
我们可以看到二次函数的RSS比一次稍好些,更高阶的函数则可以完全拟合给出的点,但是这种情况明显是不好的,因为过拟合了,太符合样本的特征了。
那如何来选择合适模型呢?如果给出的数据足够大,可以用下面方法取得更好的结果。
这其实就是我们通常用到的训练集和测试集。常用的方法有留出法、交叉验证法、自助法。这个在之前的文章中提到过,就不再赘述。
训练误差、测试误差和模型复杂度之间的关系
当然这只是一个参数的情况,实际的情况肯定是多个参数。
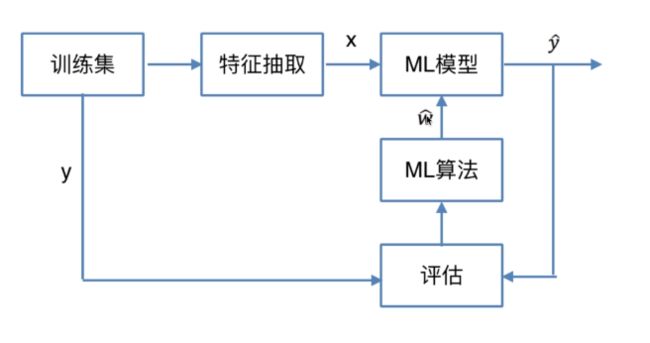
整体流程
实际案例分析
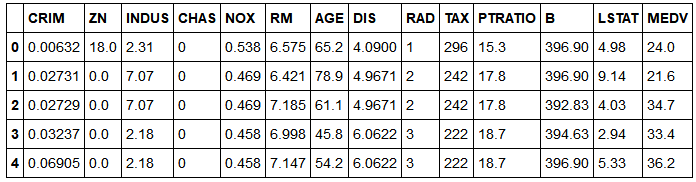
读取数据集
import pandas as pd
df = pd.read_csv('house_data.csv')
df.head()
可视化房屋数据集的特征
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(context = 'notebook')
# 人口百分比,房屋建造时间,据市中心距离,犯罪率,房屋价格,税,房间数
cols = ['LSTAT', 'AGE', 'DIS', 'CRIM', 'MEDV', 'TAX', 'RM']
sns.pairplot(df[cols], size=2.5)
plt.show()
由此我们可以看出, 房价和人口百分比成反比,与房间数成正比
通过梯度下降法计算回归参数,实现线性回归模型
关于梯度下降可以参看这篇文章
import numpy as np
class LinearRegressionByMyself(object):
def __init__(self, Learn_rate=0.001, epoch=20):
self.Learning_rate = Learn_rate
self.epoch = epoch
#训练方法
def fit(self, X, y):
#初始化参数
self.w = np.zeros(1+X.shape[1])
#误差
self.cost_list = []
for i in range(self.epoch):
#将X数据集带入回归公式
output = self.Regression_input(X)
error = y - output
self.w[1:] += self.Learning_rate * X.T.dot(error)
self.w[0] += self.Learning_rate * error.sum()
cost = (error**2).sum() / 2.0
self.cost_list.append(cost)
return self
def Regression_input(self, X):
return np.dot(X, self.w[1:])+self.w[0]
def predict(self, X):
return self.Regression_input(X)
此时需要的两个参数为X,y。X为一个二维数组,y是一个一维数组
X = df[['LSTAT']].values
y = df['MEDV'].values
在构造回归模型之前,先观察数据,发现数据相差比较大,这会对结果造成误差。我们用Scikie-learn里面的方法来实现归一化
from sklearn.preprocessing import StandardScaler
StandardScaler_x = StandardScaler()
StandardScaler_y = StandardScaler()
X_Standard = StandardScaler_x.fit_transform(X)
y_Standard = StandardScaler_y.fit_transform(y)
训练模型,拟合数据
model = LinearRegressionByMyself()
model.fit(X_Standard, y_Standard)
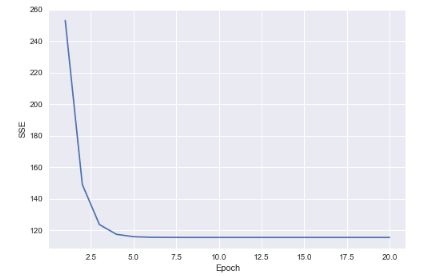
观察误差
plt.plot(range(1, model.epoch+1), model.cost_list)
plt.ylabel('SSE')
plt.xlabel('Epoch')
plt.show()
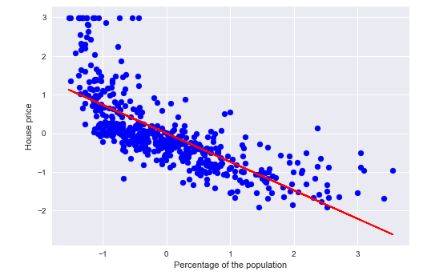
画出拟合图像
def Regression_plot(X, y, model):
plt.scatter(X, y, c='blue')
plt.plot(X, model.predict(X), color='red')
return None
Regression_plot(X_Standard, y_Standard, model)
plt.xlabel('Percentage of the population')
plt.ylabel('House price')
plt.show()
使用sklearn实现线性回归模型
from sklearn.linear_model import LinearRegression
sk_model = LinearRegression()
sk_model.fit(X, y)
print('Slope: %.3f' % sk_model.coef_[0])
print('Inercept: %.3f' % sk_model.intercept_)
Regression_plot(X, y, sk_model)
plt.xlabel('Percentage of the population')
plt.ylabel('House price')
plt.show()
评估线性回归模型
from sklearn.cross_validation import train_test_split
cols = ['LSTAT', 'AGE', 'DIS', 'CRIM', 'TAX', 'RM']
X = df[cols].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
sk_model = LinearRegression()
sk_model.fit(X_train, y_train)
y_train_predict = sk_model.predict(X_train)
y_test_predict = sk_model.predict(X_test)
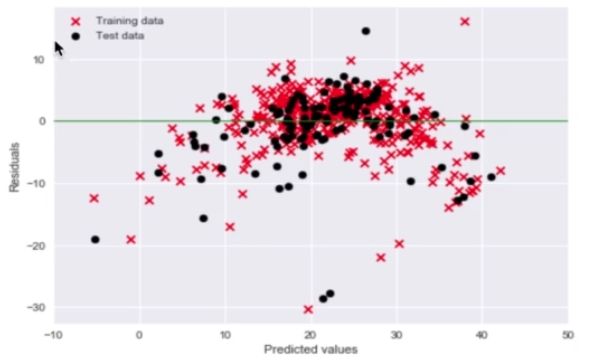
plt.scatter(y_train_predict, y_train_predict - y_train, c='red', marker='x', label='Training data')
plt.scatter(y_test_predict, y_test_predict - y_test, c='black', marker='o', label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=1, color='green')
plt.xlim([-10, 50])
plt.show()
预测值和训练值残差关系图
均方误差与R2评分
from sklearn.metrics import mean_squared_error
print('MSE train %.3f, test %.3f' % (
mean_squared_error(y_train, y_train_predict),
mean_squared_error(y_test, y_test_predict)))#MSE train 25.106, test 36.671
from sklearn.metrics import r2_score
print('R^2 train %.3f, test %.3f' % (
r2_score(y_train, y_train_predict),
r2_score(y_test, y_test_predict)))#R^2 train 0.706, test 0.551,
R2越接近1,效果越好
多项式回归
X = df[['RM']].values
y = df['MEDV'].values
Regression_model = LinearRegression()
from sklearn.preprocessing import PolynomialFeatures
quadratic = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
X_squared = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)
X_fit = np.arange(X.min(), X.max(), 0.01)[: , np.newaxis]
Linear_model = Regression_model.fit(X, y)
#拟合线性
y_line_fit = Linear_model.predict(X_fit)
linear_r2 = r2_score(y, Linear_model.predict(X))
#二次模型,先二次变换再线性回归
Squared_model = Regression_model.fit(X_squared, y)
y_quad_fit = Squared_model.predict(quadratic.fit_transform(X_fit))
quadratic_r2 = r2_score(y, Squared_model.predict(X_squared))
#三次模型
Cubic_model = Regression_model.fit(X_cubic, y)
y_cubic_fit = Cubic_model.predict(cubic.fit_transform(X_fit))
cubic_r2 = r2_score(y, Cubic_model.predict(X_cubic))
#画图
plt.scatter(X, y, label='Training point', color='lightgray')
plt.plot(X_fit, y_line_fit, label='linear, $R^2=%.2f$' % linear_r2, color='blue', lw=2, linestyle=':')
plt.plot(X_fit, y_quad_fit, label='quadratic, $R^2=%.2f$' % quadratic_r2, color='red', lw=2, linestyle='-')
plt.plot(X_fit, y_cubic_fit, label='cubic, $R^2=%.2f$' % cubic_r2, color='green', lw=2, linestyle='--')
plt.xlabel('Room number')
plt.ylabel('House price')
plt.legend(loc='upper left')
plt.show()