Question 1
Unbounded Knapsack! (无限背包)
Given a set of 'n' items having weights { W1,W2,W3,.....,Wn } & values { V1,V2,V3,.....,Vn } and a Knapsack of weight W, find the maximum value that can be accommodated using 1 or more instances of given weights. So, the aim is to maximize the value of picked up items such that sum of the weights is less than or equal to W ( Knapsack Weight ).
题目解析:
这一题不同于基础的背包问题,这里,每一件物品可以选择多次,而且重量总和是只要不超过W就可以,而不是刚好等于W.
状态转移方程:
当我们所选最优物品重量总和刚好等于 j 的时候我们可以得到下面的转移方程:
knapsack ( j ) = maximum [ knapsack ( j - W ( i ) ) + V ( i ) for i = 0, ... , n - 1]
然而当我们所选最优物品重量总和无法填满包裹时,比如总重量为10,我们选择的物品为{1,3,5}加起来为9<10.这个时候可以得到一个巧妙的状态转移方程:
knapsack ( j ) = knapsack ( j - 1 )
将两种情况合并就可以得到最终状态转移方程:
**knapsack [ j ] = max ( knapsack [ j - 1 ] , { knapsack [ j - w [ i ] ] + v [ i ] for i = 0...n-1 } ) **
实现代码如下:
weights = [1,2,3,4,5]
prices = [2,5,6,8,10]
def knapSack(j):
if j==0:
return 0
results = [0]
results.append(knapSack(j-1))
for weight in weights:
if weight<=j:
results.append(knapSack(j-weight)+prices[weights.index(weight)])
return max(results)
print(knapSack(3)) #ouput is 7
Question 2
ABA12C - Buying Apples!(二维背包)
Harish went to a supermarket to buy exactly ‘k’ kilograms apples for his ‘n’ friends. The supermarket was really weird. The pricing of items was very different. He went to the Apples section and enquired about the prices. The salesman gave him a card in which he found that the prices of apples were not per kg. The apples were packed into covers, each containing ‘x’ kg of apples, x > 0 and ‘x’ is an integer. An ‘x’ kg packet would be valued at ‘y’ rupees. So, the placard contained a table with an entry ‘y’ denoting the price of an ‘x’ kg packet. If ‘y’ is -1 it means that the corresponding packet is not available. Now as apples are available only in packets, he decides to buy atmost ‘n’ packets for his ‘n’ friends i.e he will not buy more than n packets of apples.
Harish likes his friends a lot and so he does not want to disappoint his friends. So now, he will tell you how many friends he has and you have to tell him the minimum amount of money he has to spend for his friends.
Input
The first line of input will contain the number of test cases, C. Each test case will contain two lines. The first line containing N and K, the number of friends he has and the amount of Apples in kilograms which he should buy. The second line contains K space separated integers in which the ith integer specifies the price of a ‘i’kg apple packet. A value of -1 denotes that the corresponding packet is unavailable.
0 < N <= 100
0 < K <= 100
0 < price <= 1000
Output
The output for each test case should be a single line containing the minimum amount of money he has to spend for his friends. Print -1 if it is not possible for him to satisfy his friends.
Input:
2
3 5
-1 -1 4 5 -1
5 5
1 2 3 4 5
Output:
-1
5
Explanation of test cases:
- As there are only 3 and 4kg packets in the shop, he will not be able to satisfy his friends as he would not be able to buy exactly 5kg of apples.
- He can buy five 1kg packet as he has to buy 5 kg. So the min money he should spend is 5.
题目解析:
- 小明想买k千克的苹果.
- 苹果被打包成了袋装,每袋苹果的重量与价值对应列表
[-1,-1, 4, 5, -1] - 索引就就表示苹果的重量,对应的值表示相应的价格,值为-1表示没有该重量的袋装。
- 小明想买N袋苹果,求怎么买最便宜.
这道题难在最大重量是 "exactly K",以及另外一个限制package N,导致它不同于普通的0-1背包问题,它多了一个维度N。
状态转移方程:
d[k][n] = min{d[k- price[i]][n-1] + price[i]} i = 0,1,....k-1
进行空间优化后的代码:将算过的值进行存储
import sys
mem = {}
value = {}
def useMinMoney(k,n,priceList):
#这里用一个矩阵去存储所有计算过的值,以免重复计算。
if (k,n) in value:
return value[(k,n)]
else:
if n==1:
for weight in range(1,k+1):
if weight == k:
value[(k,n)]=priceList[weight-1]
return priceList[weight-1]
value[(k,n)]=-1
return -1
results=[]
#weight
for weight in range(1,k+1):
#there is package with relative weight
if priceList[weight-1]!=-1:
# the rest of available weight is over than current package
if k==weight:
results.append(priceList[weight-1])
if k>weight:
restOfK = k - priceList[weight-1]
subtleMinMoney = useMinMoney(restOfK,n-1,priceList)
if subtleMinMoney == -1:
results.append(-1)
else:
results.append(priceList[weight-1]+subtleMinMoney)
if len(results)!=0:
return min(results)
else:
return -1
t = int(sys.stdin.readline())
output = []
for i in range(0,t):
n,k=map(int,sys.stdin.readline().split())
price = list(map(int,sys.stdin.readline().split()))
output.append(useMinMoney(k,n,price))
for i in range(0,t):
print(output[i])
Question 3
坐标系DP基础
平面上有N*M个格子,每个格子中放着一定数量的苹果。你从左上角的格子开始, 每一步只能向下走或是向右走,每次走到一个格子上就把格子里的苹果收集起来, 这样下去,你最多能收集到多少个苹果。
解这个问题与解其它的DP问题几乎没有什么两样。第一步找到问题的“状态”, 第二步找到“状态转移方程”,然后基本上问题就解决了。
首先,我们要找到这个问题中的“状态”是什么?我们必须注意到的一点是, 到达一个格子的方式最多只有两种:从左边来的(除了第一列)和从上边来的(除了第一行)。 因此为了求出到达当前格子后最多能收集到多少个苹果, 我们就要先去考察那些能到达当前这个格子的格子,到达它们最多能收集到多少个苹果。 (是不是有点绕,但这句话的本质其实是DP的关键:欲求问题的解,先要去求子问题的解)
经过上面的分析,很容易可以得出问题的状态和状态转移方程。 状态S[i][j]表示我们走到(i, j)这个格子时,最多能收集到多少个苹果。那么, 状态转移方程如下:
S[i][j]=A[i][j] + max(S[i-1][j], if i>0 ; S[i][j-1], if j>0)
伪代码如下:
For i = 0 to N - 1
For j = 0 to M - 1
S[i][j] = A[i][j] +
max(S[i][j-1], if j>0 ; S[i-1][j], if i>0 ; 0)
Output S[n-1][m-1]
Question4
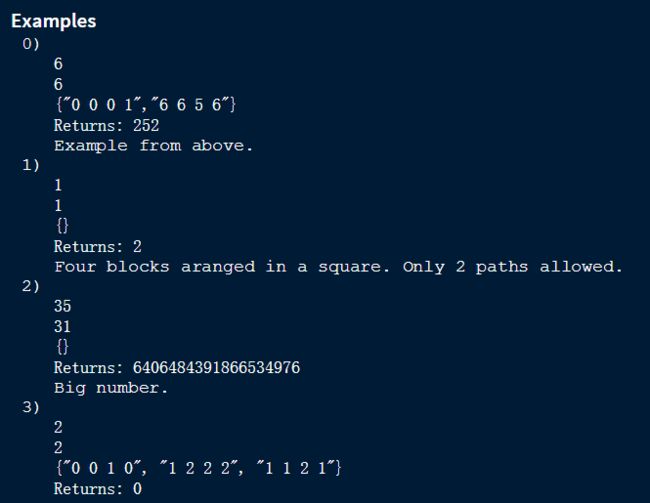
Topcoder 2003 TCO Semifinals 4 Avoid roads
In the city, roads are arranged in a grid pattern. Each point on the grid represents a corner where two blocks meet. The points are connected by line segments which represent the various street blocks. Using the cartesian coordinate system, we can assign a pair of integers to each corner as shown below.
You are standing at the corner with coordinates 0,0. Your destination is at corner width,height. You will return the number of distinct paths that lead to your destination. Each path must use exactly width+height blocks. In addition, the city has declared certain street blocks untraversable. These blocks may not be a part of any path. You will be given a String[] bad describing which blocks are bad. If (quotes for clarity) "a b c d" is an element of bad, it means the block from corner a,b to corner c,d is untraversable. For example, let's say
width = 6
length = 6
bad = {"0 0 0 1","6 6 5 6"}
The picture below shows the grid, with untraversable blocks darkened in black. A sample path has been highlighted in red.
You are standing at the corner with coordinates 0,0. Your destination is at corner width,height. You will return the number of distinct paths that lead to your destination. Each path must use exactly width+height blocks. In addition, the city has declared certain street blocks untraversable. These blocks may not be a part of any path. You will be given a String[] bad describing which blocks are bad. If (quotes for clarity) "a b c d" is an element of bad, it means the block from corner a,b to corner c,d is untraversable. For example, let's say:
width = 6
length = 6
bad = {"0 0 0 1","6 6 5 6"}
The picture below shows the grid, with untraversable blocks darkened in black. A sample path has been highlighted in red.
解题分析:
这一题和第三题一样,思路相同,多了一些限制,少了最大值要求。状态转移方程如下:
S[i][j]=S[i-1][j], if i>1 ; S[i][j-1], if j>1)
一开始编写代码时,没有考虑优化。第三个case报了runtime error,后来还是和之前一样,计算过的路径都保存起来。
代码如下:
package avoid_block;
public class AvoidRoads {
public static void main(String[] args) {
String bad1[] = {"0 0 0 1","6 6 5 6"};
System.out.println(numWays(6,6,bad1));
String bad2[] = {};
System.out.println(numWays(35,31,bad2));
}
public static long numWays(int width,int height,String[] bad){
//saveValue[width][height][0]用来判断是否计算过,0表示没有,1表示有。
//saveValue[width][height][1]用来存储值。
long[][][] saveValue=new long[width+1][height+1][2];
//splitBad数组[point1——width][point1——height][point2——width][point2——height],
//值为true表示point1和point2间有block。
boolean splitBad[][][][] = new boolean[width+1][height+1][width+1][height+1];
//处理字符串到splitBad数组中
for(int i = 0;ix2||y1>y2){
splitBad[x2][y2][x1][y1]=true;
}else if(x2>x1||y2>y1){
splitBad[x1][y1][x2][y2]=true;
}
}
return recurse(width,height,splitBad,saveValue);
}
//递归动态规划处理
public static long recurse(int width,int height,boolean block[][][][],long saveValue[][][]){
if(saveValue[width][height][0]!=0){
return saveValue[width][height][1];
}else{
long result;
if(height==0&&width==0){
result = 1;
}else if(height<0||width<0){
result = 0;
}else if(width>=1&&height>=1){
if(block[width-1][height][width][height]&&!block[width][height-1][width][height]){
result = recurse(width,height-1,block,saveValue);
}else if(!block[width-1][height][width][height]&&block[width][height-1][width][height]){
result = recurse(width-1,height,block,saveValue);
}else if(block[width-1][height][width][height]&&block[width][height-1][width][height]){
result = 0;
}else{
result = recurse(width,height-1,block,saveValue)+recurse(width-1,height,block,saveValue);
}
}else if(width>=1&&height==0){
if(block[width-1][height][width][height]){
result = 0;
}else{
result = recurse(width-1,height,block,saveValue);
}
}else{
if(block[width][height-1][width][height]){
result = 0;
}else{
result = recurse(width,height-1,block,saveValue);
}
}
saveValue[width][height][0]=1;
saveValue[width][height][1]=result;
return result;
}
}
}