《算法精解:C语言描述》笔记(一)

奥莱利为啥整俩海马当封皮?

为什么 O’Reilly 用动物形象做书籍封面

译者序(摘选)
有关数据结构和算法题材的经典书籍有很多,如《计算机程序设计艺术》,《算法导论》等,但本书绝不同于之前的相关书籍.当我们在学习数据结构和算法时,往往花费了大量的时间纠结于各种公式和理论证明上,学究气息过于浓厚而少了几分实践感.
将一个实际问题同我们学到的算法和数据结构相结合起来,这正是软件开发中的一项重要技能:抽象建模能力.
本书最大的特点是理论与实践相结合,这主要体现在以下几点上:
1.本书中的数据结构和算法实现能够以接口的形式充分得到复用
2.书中的代码实现主要以教学为目的,但也同样考虑到了实现效率的问题.
3.书中所有的应用举例都来自于真实的应用.包括操作系统中的页帧管理,页面置换算法,表达式处理等

出版时间已经超过15年之久...
问与答模块挺不错的，有三四个关于本章内容的问答题，类似于面试题，加强了印象，非常好，但问题还算能答上来，描述有点多，就不记录了，可以去看看书。

第一章概述
第二章指针操作
第三章递归
第四章算法分析
第五章链表
第六章栈和队列
第七章集合
第八章哈希表

本文代码地址

第一章概述

使用数据结构的三个原因是：
1、效率：数据结构组织数据的方式使得算法变得更加高效
2、抽象：数据结构使我们以一种更加容易理解的方式去看待数据，为解决问题提供了一层抽象概念
3、重用性：模块化且上下文无关的

使用算法的三个原因是：
1、效率：人们已经找到了许多高效的方法来解决问题
2、抽象：许多看似复杂的问题都可以用已存在的著名算法来简化
3、重用性：能在很多不同场景下重用

算法设计的一般方法：

按照算法采用的方法和思路给它们分类
随机法：依赖于随机数的统计特性。例子是快速排序

分治法：分解，将数据分解为更小，更容易管理的部分。求解，对每个分解出的部分进行处理。合并，将每部分处理的结果合并。例子是归并排序

动态规划：与分治法类似，但子问题之间并不是独立的，可能是有关系的，这本书里面没有这个例子

贪心法：在求解问题时总能做出在当前的最佳选择。不是从整体最优上考虑，而仅仅是在某种意义上的局部最优解。例子是霍夫曼编码

近似法：并不计算出最优解，只计算出“差不多好”的解。解决那些计算成本很高但又不能放弃的问题。例子是推销员问题

第二章指针操作

指针：一个指针其实只是一个变量，它存储数据在内存中的地址。
结构：结构不允许包含自身的实例，但可以包含指向自身实例的指针
数组：a[i] = * (a+i)
范型指针（void指针）：void * 可以通过void指针存储和检索任何类型的数据
指针的类型转换：a为A类型,b为B类型; a=(A * )b;
函数指针：函数名和用括号括起来，指向可执行代码段的信息块 int( match)(int * value1,int * value2)

这一章就是介绍了指针的一些基础知识

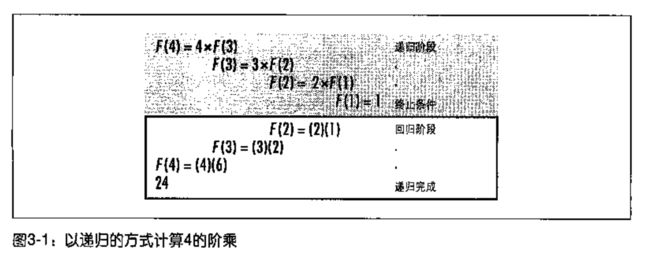
第三章递归

基本递归

用阶乘来介绍基本递归：F(n)=nF(n-1) 当n>1; F(n)=1 当n=0,n=1;
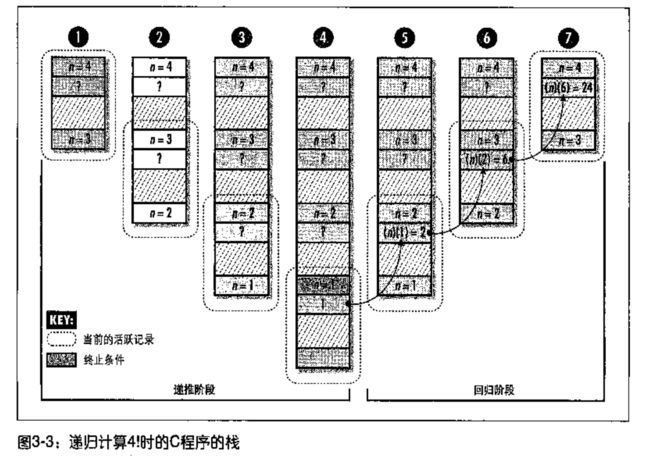
然后介绍递归的运行流程，C中函数的执行方式，C在内存中的组织方式
可执行程序由4个区域组成：
代码段：程序运行时所执行的机器指令
静态数据区：在程序生命周期内一直持久的数据，比如全局变量和静态局部变量。
堆：程序运行时动态分配的存储空间
栈：函数调用的信息。

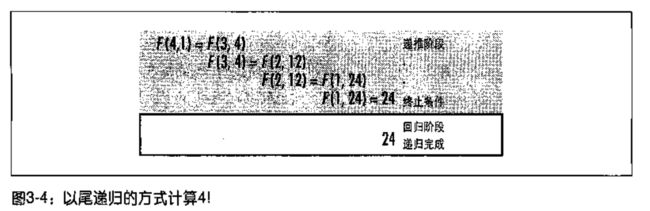
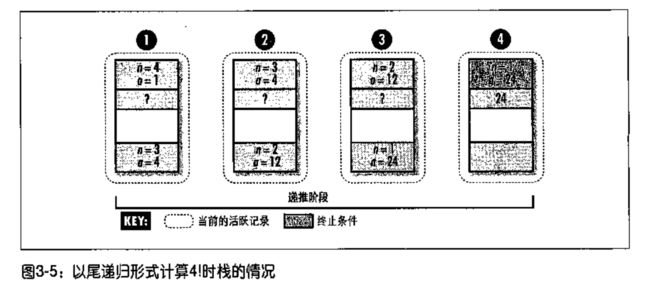
尾递归

一个函数中所有递归形式的调用都出现在函数的末尾
递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分
同样用阶乘来介绍尾递归：F(n,a)=F(n-1,na) 当n>1; F(n,a)=a 当n=0,n=1;
就是多了第二个参数a（默认为1）,a记录当前值，维护递归层次的深度，避免了每次还需要将返回值再乘以n

问与答：

1.归并排序用递归的实现：
T(n)=2T(n/2)+n 当n>1; T(n)=1 当n=1;
要注意的是判断条件要对
2.用尾递归求解整数质因子：
F(n,P)=F(n/i,PUi) 当n不为素数; F(n,P)=PUn 当n为素数;
i为n的最小质因子，P是结果集合
3.当递归的终止条件有误，永远无法满足时，会出现什么情况？
栈的增长会超过可接受的值，程序会因为栈溢出而终止运行
...

第四章算法分析

最坏情况分析：告诉我们算法性能的上限，而最好情况都是1次。
讲了下O表示法的简单规则：常数项为O(1)，忽略常量因子，两个运行时间函数加法运算取最大值，乘法结果不变
因为在函数运算次数逐渐变大的时候，这些条件占据整个运行时间的比例会越来越大，直至小的条件占比几乎被忽略
然后介绍了如何计算算法复杂度：按照算法的步骤归纳成公式，最后用O表示法简化
然后分析了下插入排序，得出插入排序的算法复杂度为O(n²)

问与答就是几个计算时间复杂度的题

第五章链表

单链表：

简称为链表，由各个元素之间通过一个指针彼此链接起来而组成。每个元素包含数据成员、next指针，指向后面的元素。
单链表只能从头到尾以一个方向进行遍历。
list文件给出了单链表的抽象数据类型定义

list文件贴出来看一下，作者整本书都是这样的风格，用代码来讲解。我认为比较重要的就贴出来，其他的还是下载源码查看吧，太多了。
不过如果有需要的话可以留言，我可以全部贴出来

//  list.h
//链表抽象数据类型

#ifndef list_h
#define list_h

#include 

typedef struct ListElmt_{
    void *data;
    struct ListElmt_ *next;
}ListElmt;

typedef struct List_{
    int size;
    int (*math)(const void *key1,const void *key2);
    void (*destroy)(void *data);
    ListElmt *head;
    ListElmt *tail;
}List;

//初始化一个链表 O(1)
void list_init(List *list,void (*destroy)(void *data));

//销毁链表 O(n)
void list_destroy(List *list);

//在链表list的element后面插入一个新元素,如果element为NULL，代表插入 头部 O(1)
int list_ins_next(List *list,ListElmt *element,const void *data);

//移除链表list的element后面的元素，如果element为NULL，则移除链表头元素 O(1)
int list_rem_next(List *list,ListElmt *element,void **data);

//以下宏皆为O(1)
//返回list中元素的个数
int list_size(const List *list);
//返回list中头元素的指针
ListElmt *list_head(const List *list);
//返回list中尾元素的指针
ListElmt *list_tail(const List *list);
//判断element是否为头结点
int list_is_head(const ListElmt *element);
//判断element是否为尾结点
int list_is_tail(const ListElmt *element);
//element中保存的数据
void *list_data(const ListElmt *element);
//element的下一个结点
ListElmt *list_next(const ListElmt *element);

#define list_size(list) ((list)->size)
#define list_head(list) ((list)->head)
#define list_tail(list) ((list)->tail)
#define list_is_head(list,element) ((element) == (list)->head?1:0)
#define list_is_tail(element) ((element)->next == NULL?1:0)
#define list_data(element) ((element)->data)
#define list_next(element) ((element)->next)

#endif /* list_h */

#include "list.h"
#include 
#include 

//初始化一个链表
void list_init(List *list,void (*destroy)(void *data))
{
    list->size = 0;
    list->destroy = destroy;
    list->head = NULL;
    list->tail = NULL;
    return;
}

//销毁链表
void list_destroy(List *list)
{
    void *data;
    //每个元素都调用一次
    while (list_size(list)>0)
    {
        if (list_rem_next(list, NULL, (void **)&data)==0 && list->destroy != NULL)
        {
            list_destroy(data);
        }
    }
    //将list中当前位置后面的n个字节用0替换并返回list
    memset(list,0,sizeof(List));
    return;
}

//在链表list的element后面插入一个新元素
int list_ins_next(List *list,ListElmt *element,const void *data)
{
    ListElmt *new_element;
    if ((new_element = (ListElmt *)malloc(sizeof(ListElmt))) == NULL)
    {
        return -1;
    }
    new_element->data = (void *)data;
    //当新的元素将插入链表头部
    if (element == NULL)
    {
        if (list_size(list) == 0)
        {
            list->tail = new_element;
        }
        //一般是将新元素的next指针指向它之后的那个元素，
        //然后将新元素位置之前的结点next指针指向新插入的元素
        new_element->next = list->head;
        list->head = new_element;
    }
    else
    {
        if (element->next == NULL)
        {
            list->tail = new_element;
        }
        new_element->next = element->next;
        element->next = new_element;
    }
    list->size++;
    return 0;
}

//移除链表list的element后面的元素
int list_rem_next(List *list,ListElmt *element,void **data)
{
    ListElmt *old_element;
    if (list_size(list) == 0)
    {
        return -1;
    }
    //移除头结点
    if (element == NULL)
    {
        //将要移除的目标节点前一个元素的next指针指向目标节点下一个元素
        *data = list->head->data;
        old_element = list->head;
        list->head = list->head->next;
        //当移除操作使整个链表称为空链表
        if (list_size(list) == 1)
        {
            list->tail = NULL;
        }
    }
    else
    {
        if (element->next == NULL)
        {
            return -1;
        }
        *data = element->next->data;
        old_element = element->next;
        element->next = element->next->next;
        if (element->next == NULL)
        {
            list->tail = element;
        }
    }
    
    free(old_element);
    list->size--;
    return 0;
}

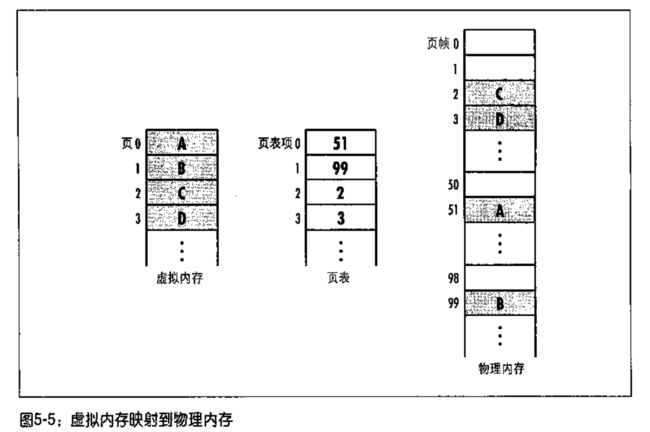
链表的应用：管理页帧
frames文件是使用链表管理页帧的例子
在一些支持虚拟内存的系统中，用链表来管理页帧是非常好的办法，因为页帧的分配将涉及频繁的插入和删除操作，而且这些操作都发生在链表头
虚拟内存：一种地址空间的映射机制，它允许进程不必完全加载到物理内存（系统的实际内存）中也可以运行。优点是进程可以使用比物理内存大得多的空间，多个进程能够共享系统的内存以并发的方式执行。
而运行虚拟内存下的进程需要处理虚拟地址，必须由操作系统做转换，每一个进程都有自己的页表，将虚拟地址空间中的页映射到物理内存中的页帧上。

对于开发来说可能用处不大，不过可以更好的理解链表的使用

双向链表：

链表元素之间由两个指针链接。每个元素包含数据成员、next指针、prev指针，指向前驱元素。

双向链表书上没有例子与应用，直接看看源码dlist文件吧

循环链表：

有尾部元素的链表，可以是单向的或双向的，源码clist文件

循环链表的应用：第二次机会页面置换法
第二次机会页面置换法，也称时钟算法，是最近最少使用算法（也称为LRU页面替换法，Least Recenty Used）
跟随上面,是系统管理内存页帧分配的例子，解决空闲页面链表为空时，系统为其分配新的页帧。
大概就是当需要某个页帧时，系统遍历链表，找到上次遍历没有被系统访问过的页面，因为最后要回到遍历开始的页面，所以循环链表最适合。
作者花了一整页篇幅来讲解，但我认为对于开发来说可能用处不大，建议看看源码page文件即可

问与答：

1、数组与链表的使用情况：
进行频繁的插入和删除时，链表更适合，而数组的元素是连续排列的，更适合通过索引查找
2、链表的增删改查与数组相比有何差异？
的确，链表除了销毁操作之外，其他操作都是O(1)，但是都需要一个想要操作的元素指针，而得到该指针的代价是很高的，需要遍历链表
插入本身复杂度是O(1)，但是访问特定位置的元素复杂度是O(n)
3、为什么单链表和循环链表不能指定移除该元素，而是该元素下一个元素？
因为没有指向前驱结点的指针，所以找不到前驱结点来指向被移除元素的后继结点。
...

第六章栈和队列

栈

后进先出，羽毛球筒
作者使用链表实现栈的，调用的链表的实现方法

stack文件

#ifndef stack_h
#define stack_h

#include 
#include "list.h"

typedef List Stack;

#define stack_init list_init
#define stack_destroy list_destroy


//向stack中压入一个元素 O(1)
int stack_push(Stack *stack,const void *data);
//从stack中弹出一个元素 O(1)
int stack_pop(Stack *stack,void **data);
//皆为 O(1)
//获取栈顶部的元素
void *stack_peek(const Stack *stack);
//获取栈中元素个数
int stack_size(const Stack *stack);

//获取顶元素的信息
#define stack_peek(stack) ((stack)->head == NULL?NULL:(stack)->head->data)
#define stack_size list_size

#endif /* stack_h */

#include "stack.h"

//向stack中压入一个元素 O(1)
int stack_push(Stack *stack,const void *data)
{
    return list_ins_next(stack, NULL, data);
}
//从stack中弹出一个元素 O(1)
int stack_pop(Stack *stack,void **data)
{
    return list_rem_next(stack, NULL, data);
}

队列

先进先出，排队
作者也是使用链表来实现队列的，调用的队列的实现方法

#include "queue.h"

int queue_enqueue(Queue *queue,const void *data)
{
    return list_ins_next(queue, list_tail(queue), data);
}

int queue_dequeue(Queue *queue,void **data)
{
    return list_rem_next(queue, NULL, data);
}

作者用事件驱动来举例队列的作用，因为计算机的应用主要遵循的是实时发生的顺序来执行，需要有序地存储和管理事件。
当告知应用程序有事件将进行处理时，将一个事件入队，当应用程序认为是时候处理一个事件时，将一个事件出队

问与答：

1、从一个队列中删除一些元素，剩下的按顺序留在队列中，用队列和链表如何处理
队列：从头开始出队，不删除的出队后再入队
链表：遍历，遍历到元素后用list_rem_next函数删除即可

第七章集合

集合是不同对象的无序聚集。成员是无序的，每个成员都只在集合中出现一次
是数学中集合的概念，有子集，并集，空集等等，操作也是交集，并集，差集等
作者也是使用链表来实现的，所以很多函数需要遍历，性能适合小型到中等规模的集合数据
(Set的代码在github中)

集合的应用：集合覆盖
在一群选手中挑选人员组建出一支队伍，每名选手都有特定的技能组合。目标是组建出人数最少，但所有技能都有的队伍。
技能集合S={a,b,c,d,e}
选手集合P={A1，A2，A3，A4}
组合集合为：A1={a,b} A2={c,d,e} A3={a,b,c,d} A4={a}
最佳集合应为C={A1，A2}
但算法的结果为C={A3，A2,A1}

#ifndef cover_h
#define cover_h

#include 
#include "set.h"

typedef struct KSet_{
    void *key;
    Set set;
}KSet;

int cover(Set *members,Set *subsets,Set *covering);

#endif /* cover_h */

#include "cover.h"

int cover(Set *members,Set *subsets,Set *covering)
{
    Set intersection;
    KSet *subset;
    ListElmt *member;
    ListElmt *max_member=NULL;
    void *data;
    int max_size;
    
    set_init(covering, subsets->math, NULL);
    while (set_size(members)>0 && set_size(subsets) > 0)
    {
        max_size = 0;
        for (member = list_head(subsets); member !=NULL; member = list_next(member))
        {
            if (set_intersection(&intersection, &((KSet *)list_data(member))->set, members) != 0)
            {
                return -1;
            }
            
            if (set_size(&intersection) > max_size)
            {
                max_member = member;
                max_size = set_size(&intersection);
            }
            set_destroy(&intersection);
        }
        
        if (max_size == 0)
        {
            return 1;
        }
        
        subset = (KSet *)list_data(max_member);
        
        if (set_insert(covering, subset) != 0)
        {
            return -1;
        }
        
        for (member=list_head(&((KSet *)list_data(max_member))->set); member!=NULL; member=list_next(member))
        {
            data = list_data(member);
            if (set_remove(members, (void **)&data)==0
                &&members->destroy != NULL)
            {
                members->destroy(data);
            }
        }
        
        if (set_remove(subsets, (void **)&subset) != 0)
        {
            return -1;
        }
       
    }
    if (set_size(members)>0)
    {
        return -1;
    }
     return 0;
}

是一种优化求解问题
每次开始都在subsets中找出能够覆盖到members的最大交集，然后加到covering中，所以有可能解会有小小的多余，是一种近似最优解
int cover(Set *members,Set *subsets,Set *covering);
members为S，subsets为P中的子集如A1， covering为C

第八章哈希表

散列表，通过一个哈希函数，在所有可能的键与槽位之间建立一张映射表。

1 链式哈希表

由一组链表构成，每个链表都可以看做一个桶，所有的元素通过散列的方式放到具体的不同的桶中

#ifndef chtbl_h
#define chtbl_h

#include 
#include "list.h"

typedef struct CHTbl_{
    int buckets;//桶数
    int (*h)(const void *key);
    int (*match)(const void *key1,const void *key2);
    void (*destroy)(void *data);
    int size;
    List *table;
}CHTbl;

//buckets为桶数，
//h指向哈希函数，会将键散列
//match判断两个键是否匹配
//destroy销毁
int chtbl_init(CHTbl *htbl,int buckets,int(*h)(const void *key),int(*match)(const void *key1,const void *key2),void(*destroy)(void *data));

//销毁，删除每个桶中的元素
void chtbl_destroy(CHTbl *htbl);
int chtbl_insert(CHTbl *htbl,const void *data);
int chtbl_remove(CHTbl *htbl,void **data);
//查找
int chtbl_lookup(const CHTbl *htbl,void **data);

#define chtbl_size(htbl) ((htbl)->size)

#endif /* chtbl_h */

#include "chtbl.h"
#include 
#include 

int chtbl_init(CHTbl *htbl,int buckets,int(*h)(const void *key),int(*match)(const void *key1,const void *key2),void(*destroy)(void *data))
{
    if ((htbl->table = (List *)malloc(buckets *sizeof(List))) == NULL)
    {
        return -1;
    }
    htbl->buckets = buckets;
    for (int i=0; ibuckets; i++)
    {
        list_init(&htbl->table[i], destroy);
    }
    
    htbl->h = h;
    htbl->match = match;
    htbl->destroy = destroy;
    
    htbl->size = 0;
    return 0;
}

//销毁，删除每个桶中的元素
void chtbl_destroy(CHTbl *htbl)
{
    for (int i=0; ibuckets; i++)
    {
        list_destroy(&htbl->table[i]);
    }
    free(htbl->table);
    memset(htbl, 0, sizeof(CHTbl));
    return;
}

int chtbl_insert(CHTbl *htbl,const void *data)
{
    void *temp;
    int bucket,retval;
    temp = (void *)data;
    //判断是否已经存在
    if (chtbl_lookup(htbl, &temp) == 0)
    {
        return 1;
    }
    //哈希key
    bucket = htbl->h(data) % htbl->buckets;
    //插入
    if((retval=list_ins_next(&htbl->table[bucket], NULL, data))==0)
    {
        htbl->size++;
    }
    return retval;
}

int chtbl_remove(CHTbl *htbl,void **data)
{
    ListElmt *element,*prev;
    int bucket;
    //哈希key
    bucket = htbl->h(data) % htbl->buckets;
    prev = NULL;
    for (element = list_head(&htbl->table[bucket]); element != NULL; element = list_next(element))
    {
        if (htbl->match(*data,list_data(element)))
        {
            if (list_rem_next(&htbl->table[bucket], prev, data)==0)
            {
                htbl->size--;
                return 0;
            }else{
                return -1;
            }
        }
        prev = element;
    }
    return -1;
}

//查找
int chtbl_lookup(const CHTbl *htbl,void **data)
{
    ListElmt *element;
    int bucket;
    //哈希key
    bucket = htbl->h(data) % htbl->buckets;
    for (element = list_head(&htbl->table[bucket]); element != NULL; element = list_next(element))
    {
        if (htbl->match(*data,list_data(element)))
        {
            *data = list_data(element);
            return 0;
        }
    }
    return -1;
}

解决冲突
两个键散列到一个相同的槽位时，两个键之间会产生冲突
链式哈希表就直接将元素放入桶中，但桶有可能越来越大
一个好的哈希函数会尽可能做到均匀散列
h(k) = m 一般k为整型

转换键的方法：
取余法：计算k除以m的所得到的余数，将k映射到m槽位
h(k)=k mod m

乘法：将整型键k乘以一个常数A(0

链式哈希表的应用：符号表
在编译器中用来维护程序中出现的符号信息。
编译器在翻译时，为了能够更加有效地管理程序中的符号信息，使用符号表

2 开地址哈希表

元素存放在表本身，用于依赖于固定大小表的应用

#ifndef ohtbl_h
#define ohtbl_h

#include 

typedef struct OHTbl_{
    int     positions;//哈希表中分配的槽位数目
    void    *vacated;//曾经删除的一个元素
    
    int     (*h1)(const void *key);
    int     (*h2)(const void *key);
    int     (*match)(const void *key1,const void *key2);
    void    (*destroy)(void *data);
    
    int     size;
    void    **table;//存储元素的数组
}OHTbl;


//positions为槽位的个数
//h1，h2指向哈希函数，会将键散列
//match判断两个键是否匹配
//destroy销毁
int ohtbl_init(OHTbl *htbl,int positions,int(*h1)(const void *key),int(*h2)(const void *key),int(*match)(const void *key1,const void *key2),void(*destroy)(void *data));

//销毁
void ohtbl_destroy(OHTbl *htbl);
int ohtbl_insert(OHTbl *htbl,const void *data);
int ohtbl_remove(OHTbl *htbl,void **data);
//查找
int ohtbl_lookup(const OHTbl *htbl,void **data);

#define ohtbl_size(htbl) ((htbl)->size)


#endif /* ohtbl_h */

#include "ohtbl.h"
#include 
#include 

static char vacated;

int ohtbl_init(OHTbl *htbl,int positions,int(*h1)(const void *key),int(*h2)(const void *key),int(*match)(const void *key1,const void *key2),void(*destroy)(void *data))
{
    if ((htbl->table = (void **)malloc(positions *sizeof(void *))) == NULL)
    {
        return -1;
    }
    htbl->positions = positions;
    for (int i=0; ipositions; i++)
    {
        htbl->table[i] = NULL;
    }
    htbl->vacated = &vacated;
    htbl->h1 = h1;
    htbl->h2 = h2;
    htbl->match = match;
    htbl->destroy = destroy;
    htbl->size = 0;
    return 0;
}

//销毁
void ohtbl_destroy(OHTbl *htbl)
{
    if (htbl->destroy != NULL)
    {
        for (int i=0; ipositions; i++)
        {
            if (htbl->table[i] != NULL && htbl->table[i] != htbl->vacated)
            {
                htbl->destroy(htbl->table[i]);
            }
        }
    }
    free(htbl->table);
    memset(htbl,0,sizeof(OHTbl));
    return;
}

int ohtbl_insert(OHTbl *htbl,const void *data)
{
    void *temp;
    int position;
    if (htbl->size == htbl->positions)
    {
        return -1;
    }
    temp = (void *)data;
    if (ohtbl_lookup(htbl, &temp)==0)
    {
        return 1;
    }
    for (int i=0; ipositions; i++)
    {
        position = (htbl->h1(data)+(i*htbl->h2(data))) % htbl->positions;
        if (htbl->table[position]==NULL || htbl->table[position] == htbl->vacated)
        {
            htbl->table[position] = (void *)data;
            htbl->size++;
            return 0;
        }
    }
    return -1;
}


int ohtbl_remove(OHTbl *htbl,void **data)
{
    int position;
    for (int i=0; ipositions; i++)
    {
        position = (htbl->h1(*data) + (i*htbl->h2(*data))) % htbl->positions;
        if (htbl->table[position] == NULL)
        {
            return -1;
        }
        else if (htbl->table[position] == htbl->vacated)
        {
            continue;
        }
        else if (htbl->match(htbl->table[position],*data))
        {
            *data = htbl->table[position];
            htbl->table[position] = htbl->vacated;
            htbl->size--;
            return 0;
        }
    }
    return -1;
}
//查找
int ohtbl_lookup(const OHTbl *htbl,void **data)
{
    int position;
    for (int i=0; ipositions; i++)
    {
        position = (htbl->h1(*data) + (i*htbl->h2(*data))) % htbl->positions;
        if (htbl->table[position] == NULL)
        {
            return -1;
        }
        else if (htbl->match(htbl->table[position],*data))
        {
            *data = htbl->table[position];
            return 0;
        }
    }
    return -1;
}

解决冲突
探查这个表，直到找到一个可以放置元素的槽
探查槽位的哈希函数定义为：h(k,i)=x
k是键，i是探查的次数，x是得到的哈希编码

线性探查
用哈希函数定位到某一数值后探查表中连续的槽位
h(k,i) = (h(k)+i) mod m
双散列
通过计算两个辅助哈希函数哈希编码的和来得到哈希编码
h(k,i) = (h1(k)+ih2(k)) mod m
h1与h2为两个辅助哈希函数，能够在表中探查并产生较好的元素分布

问与答：

1、链式哈希表的最坏性能？如何保证不会发生？
所有元素全部散列在一个桶中时，性能最差
选择一个好的哈希函数
2、开地址哈希表的最坏性能？如何保证不会发生？
表已经满了，而且要查找的元素不在此表中，性能最差
不要让元素的个数超过表容量的80%

《算法精解:C语言描述》笔记(一)

第一章概述

算法设计的一般方法：

第二章指针操作

第三章递归

基本递归

尾递归

问与答：

第四章算法分析

相关扩展：

第五章链表

单链表：

双向链表：

循环链表：

问与答：

第六章栈和队列

栈

队列

问与答：

第七章集合

第八章哈希表

1 链式哈希表

2 开地址哈希表

问与答：

你可能感兴趣的:(《算法精解:C语言描述》笔记(一))

《算法精解:C语言描述》笔记(一)

第一章 概述

算法设计的一般方法：

第二章 指针操作

第三章 递归

基本递归

尾递归

问与答：

第四章 算法分析

相关扩展：

第五章 链表

单链表：

双向链表：

循环链表：

问与答：

第六章 栈和队列

栈

队列

问与答：

第七章 集合

第八章 哈希表

1 链式哈希表

2 开地址哈希表

问与答：

你可能感兴趣的:(《算法精解:C语言描述》笔记(一))

第一章概述

第二章指针操作

第三章递归

第四章算法分析

第五章链表

第六章栈和队列

第七章集合

第八章哈希表