- 扫地机类清洁产品之直流无刷电机控制
悟空胆好小
清洁服务机器人单片机人工智能
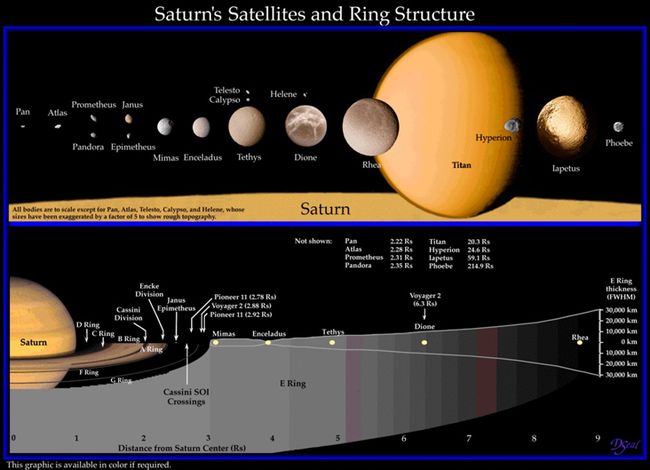
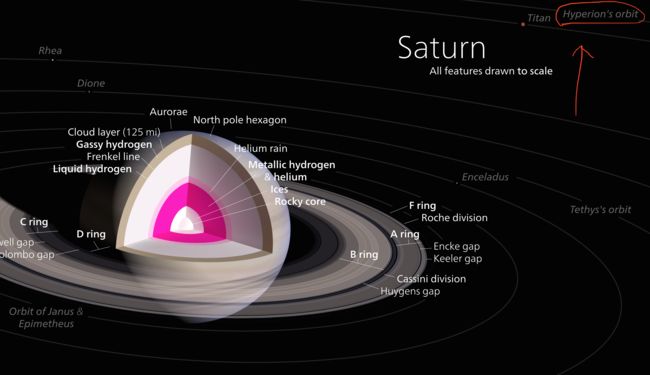
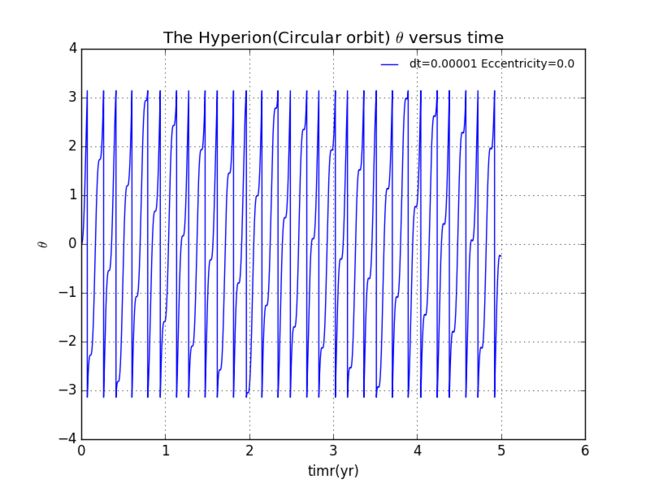
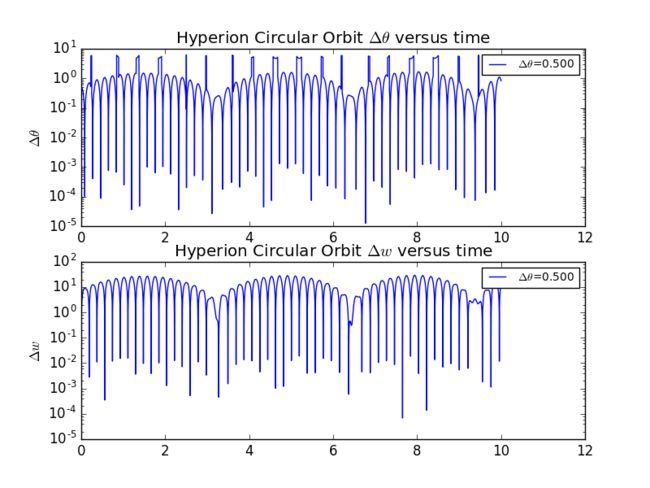
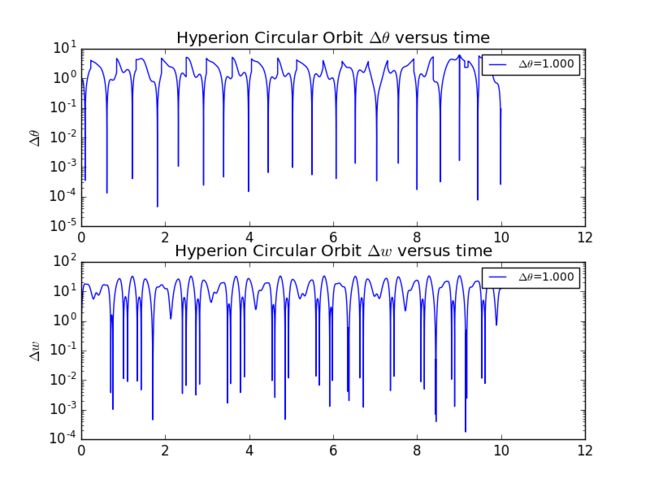
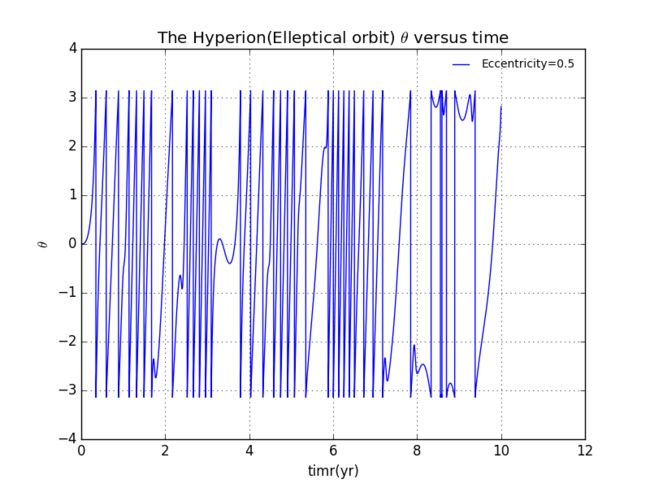
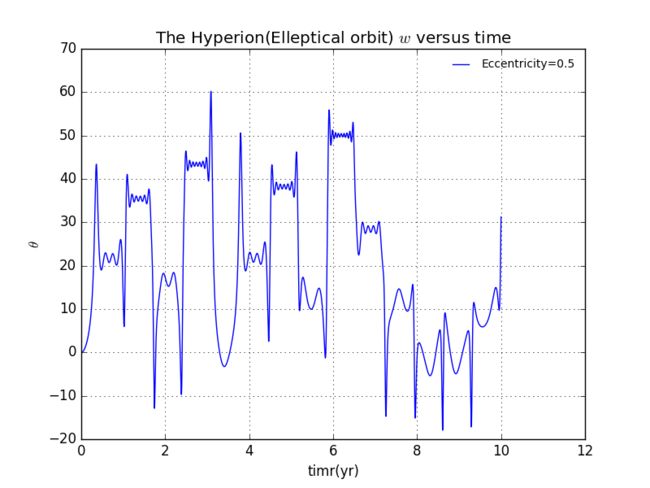
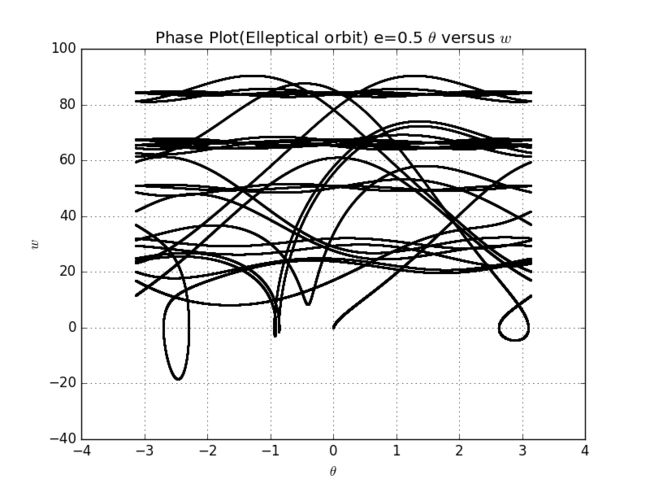
扫地机类清洁产品之直流无刷电机控制1.1前言扫地机产品有很多的电机控制,滚刷电机1个,边刷电机1-2个,清水泵电机,风机一个,部分中高端产品支持抹布功能,也就是存在抹布盘电机,还有追觅科沃斯石头等边刷抬升电机,滚刷抬升电机等的,这些电机有直流有刷电机,直接无刷电机,步进电机,电磁阀,挪动泵等不同类型。电机的原理,驱动控制方式也不行。接下来一段时间的几个文章会作个专题分析分享。直流有刷电机会自动持续
- 向内而求
陈陈_19b4
10月27日,阴。阅读书目:《次第花开》。作者:希阿荣博堪布,是当今藏传佛家宁玛派最伟大的上师法王,如意宝晋美彭措仁波切颇具影响力的弟子之一。多年以来,赴海内外各地弘扬佛法,以正式授课、现场开示、发表文章等多种方法指导佛学弟子修行佛法。代表作《寂静之道》、《生命这出戏》、《透过佛法看世界》自出版以来一直是佛教类书籍中的畅销书。图片发自App金句:1.佛陀说,一切痛苦的根源在于我们长期以来对自身及外
- 那个抄袭的大张伟
猫小努
最近一直在追《即刻电音》这个综艺,除了觉得出场节目的音乐制作人有意思之外,也觉得有两个导师挺有趣的(另外一个就忽略了吧)。孙艺兴在上一篇文章里面已经说过了,那么这篇就说说我们的大老师,大张伟吧。其实在节目刚开始大张伟出来的时候,我以为他是属于导师里面来活跃气氛负责搞笑的,毕竟孙艺兴属于卖萌卖傻卖老实的,尚雯婕一般负责装逼耍狠的,而大张伟一贯以来上综艺的形象基本上都是蹦蹦跳跳带动气氛的。谁知道,两期
- 【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
- Python中os.environ基本介绍及使用方法
鹤冲天Pro
#Pythonpython服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- DIV+CSS+JavaScript技术制作网页(旅游主题网页设计与制作)云南大理
STU学生网页设计
网页设计期末网页作业html静态网页html5期末大作业网页设计web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业:【HTML5网页期末作业(1000套)】程序员有趣的告白方式:【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面:计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
- 探索OpenAI和LangChain的适配器集成:轻松切换模型提供商
nseejrukjhad
langchaineasyui前端python
#探索OpenAI和LangChain的适配器集成:轻松切换模型提供商##引言在人工智能和自然语言处理的世界中,OpenAI的模型提供了强大的能力。然而,随着技术的发展,许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具,集成了多种模型提供商,通过提供适配器,简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成,以便轻松切换模型提供商
- 想明白这个问题,你才能写下去
文自拾
春节放假的时候,又有一天梦见她,第二天她冒着漫天大雪,傻傻地跑来见我。她说,见见傻傻的我,天很冷,心很暖。她回去后,我写了一篇文章,题目叫——从此梦中只有你。我们没在一起的很长一段时间里,她都在我的心底,一次次出现在我的梦里。我对她说,在一起之前,是胆小且闷骚,在一起之后,我变得不要脸了。不要脸的——去爱你。那文章没写完,火车上,给她看了。我有点小失望,花了好几个小时写,她分分钟就看完,很希望她逐
- HTML网页设计制作大作业(div+css) 云南我的家乡旅游景点 带文字滚动
二挡起步
web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript:做与用户的交互行为文章目录前端学习路线
- 每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
- libyuv之linux编译
jaronho
Linuxlinux运维服务器
文章目录一、下载源码二、编译源码三、注意事项1、银河麒麟系统(aarch64)(1)解决armv8-a+dotprod+i8mm指令集支持问题(2)解决armv9-a+sve2指令集支持问题一、下载源码到GitHub网站下载https://github.com/lemenkov/libyuv源码,或者用直接用git克隆到本地,如:gitclonehttps://github.com/lemenko
- 冬天短期的暴利小生意有哪些?那些小生意适合新手做?
一起高省
短期生意不失为创业的一个商机,不过短期生意的商机是转瞬即逝的,而且这类生意也很难作为长期的生意去做,那冬天短期暴利小生意查看更多关于短期暴利小生意的文章有哪些呢?给大家先推荐一个2023年风口项目吧,真很不错的项目,全程零投资,当做副业来做真的很稳定,不管你什么阶层的人,或多或少都网购吧?你们知道网购是可以拿提成,拿返利,拿分佣的吗?你们知道很多优惠券群里面,天天群主和管理发一些商品吗?他们其实在
- Python 实现图片裁剪(附代码) | Python工具
剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法,一如既往的实用主义。环境依赖ffmpeg环境安装,可以参考我的另一篇文章:windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg,而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装:pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了,上代码
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(4)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例:文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片(Slicing)操作**基本切片语法
- 【华为OD技术面试真题 - 技术面】-测试八股文真题题库(1)
算法大师
华为od面试python算法前端
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.黑盒测试和白盒测试的区别2.假设我们公司现在开发一个类似于微信的软件1.0版本,现在要你测试这个功能:打开聊天窗口,输入文本,限制字数在200字以内。问你怎么提取测试点。功能测试性能测试安全性测试可用性测试跨平台兼容性测试网络环境测试3.接口测试的工具你了解哪些
- Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
- 【无标题】达瓦达瓦
JhonKI
考研
博客主页:https://blog.csdn.net/2301_779549673欢迎点赞收藏⭐留言如有错误敬请指正!本文由JohnKi原创,首发于CSDN未来很长,值得我们全力奔赴更美好的生活✨文章目录前言111️111❤️111111111111111总结111前言111骗骗流量券,嘿嘿111111111111111111111111111️111❤️111111111111111总结11
- 上图为是否色发
JhonKI
考研
博客主页:https://blog.csdn.net/2301_779549673欢迎点赞收藏⭐留言如有错误敬请指正!本文由JohnKi原创,首发于CSDN未来很长,值得我们全力奔赴更美好的生活✨文章目录前言111️111❤️111111111111111总结111前言111骗骗流量券,嘿嘿111111111111111111111111111️111❤️111111111111111总结11
- 【Git】常见命令(仅笔记)
好想有猫猫
GitLinux学习笔记git笔记elasticsearchlinuxc++
文章目录创建/初始化本地仓库添加本地仓库配置项提交文件查看仓库状态回退仓库查看日志分支删除文件暂存工作区代码远程仓库使用`.gitigore`文件让git不追踪一些文件标签创建/初始化本地仓库gitinit添加本地仓库配置项gitconfig-l#以列表形式显示配置项gitconfiguser.name"ljh"#配置user.namegitconfiguser.email"
[email protected]
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(1)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归(LinearRegression)模型形式:关键点:逻辑回归(LogisticRegression)模型形式:关键点:参数估计与评估:3.python浅拷贝及深拷贝浅拷贝(Shal
- 143234234123432
JhonKI
考研
博客主页:https://blog.csdn.net/2301_779549673欢迎点赞收藏⭐留言如有错误敬请指正!本文由JohnKi原创,首发于CSDN未来很长,值得我们全力奔赴更美好的生活✨文章目录前言111️111❤️111111111111111总结111前言111骗骗流量券,嘿嘿111111111111111111111111111️111❤️111111111111111总结11
- 道阻且长,行则将至
sweet橘子
本文参与书香澜梦主题征文“行”文章原创首发,文责自负。我们每一个人都应该有属于自己的愿望或者是理想,人一但有了理想也就算是有了方向,它就会像灯塔一样指引我们前进的方向,哪怕是再远大的理想,如果坚持,那么我相信它就一定有收获。屈原是我最喜欢的一个浪漫主义的诗人,他曾今说过:“路漫漫其修远兮,吾将上下而求索。”人生的道路很长,但是为了实现自己的理想抱负我愿意付出我毕生的精力,只专注这一件事,因为“道阻
- 4招写出高价值文章
zhiliner
文章写得泛泛是因为思考得不够深,思考得越深文章会越有价值。拿到一个主题一定要去深入挖掘事件背后的东西,比如人物困境以及趋势性的东西。写作过程中有几个深度思考的方法一、解剖,让旧素材焕发新意作为一个写作者,我们能够做的最大贡献,就是给出自己看世界的角度。解剖其实就是把这个话题相关的信息都列出来,详细的列出来,看清楚它的内部。我们看到一个老话题或者一段旧素材的时候,不要只看这个素材或者话题本身,一定要
- 【六】阿伟开始搭建Kafka学习环境
能源恒观
中间件学习kafkaspring
阿伟开始搭建Kafka学习环境概述上一篇文章阿伟学习了Kafka的核心概念,并且把市面上流行的消息中间件特性进行了梳理和对比,方便大家在学习过程中进行对比学习,最后梳理了一些Kafka使用中经常遇到的Kafka难题以及解决思路,经过上一篇的学习我相信大家对Kafka有了初步的认识,本篇将继续学习Kafka。一、安装和配置学习一项技术首先要搭建一套服务,而Kafka的运行主要需要部署jdk、zook
- ExpRe[25] bash外的其它shell:zsh和fish
tritone
ExpRebashlinuxubuntushell
文章目录zsh基础配置实用特性插件`autojump`语法高亮自动补全fish优点缺点时效性本篇撰写时间为2021.12.15,由于计算机技术日新月异,博客中所有内容都有时效和版本限制,具体做法不一定总行得通,链接可能改动失效,各种软件的用法可能有修改。但是其中透露的思想往往是值得学习的。本篇前置:ExpRe[10]Ubuntu[2]准备神秘软件、备份恢复软件https://www.cnblogs
- openssl+keepalived安装部署
_小亦_
项目部署keepalivedopenssl
文章目录OpenSSL安装下载地址编译安装修改系统配置版本Keepalived安装下载地址安装遇到问题安装完成配置文件keepalived运行检查运行状态查看系统日志修改服务service重新加载systemd检查配置文件语法错误OpenSSL安装下载地址考虑到后面设备可能没法连接到外网,所以采用安装包的方式进行部署,下载地址:https://www.openssl.org/source/old/
- 关于Mysql 中 Row size too large (> 8126) 错误的解决和理解
秋刀prince
mysqlmysql数据库
提示:啰嗦一嘴,数据库的任何操作和验证前,一定要记得先备份!!!不会有错;文章目录问题发现一、问题导致的可能原因1、页大小2、行格式2.1compact格式2.2Redundant格式2.3Dynamic格式2.4Compressed格式3、BLOB和TEXT列二、解决办法1、修改页大小(不推荐)2、修改行格式3、修改数据类型为BLOB和TEXT列4、其他优化方式(可以参考使用)4.1合理设置数据
- 一颗小桃树
李蓉乐平市湾头中小学
当“凹”同“洼”的时侯,才读(wa,平声),他不叫贾平洼(贾,原名贾平娃),非要写作贾平凹。为了表示对他的尊重,对文学的尊重,对文化人的尊重。如果不是帮闺蜜的儿子修改作文,我也不会发现贾平凹叫贾平娃。以下是摘选他的文章《一棵小桃树》:可我的小桃树儿,一颗“仙桃”的种子,却开得太白了,太淡了,那瓣片儿单薄得似纸做的,没有肉的感觉,没有粉的感觉,像患了重病的少女,苍白白的脸,又偏苦涩涩地笑着。雨还在下
- 【从浅识到熟知Linux】Linux发展史
Jammingpro
从浅学到熟知Linuxlinux运维服务器
归属专栏:从浅学到熟知Linux个人主页:Jammingpro每日努力一点点,技术变化看得见文章前言:本篇文章记录Linux发展的历史,因在介绍Linux过程中涉及的其他操作系统及人物,本文对相关内容也有所介绍。文章目录Unix发展史Linux发展史开源Linux官网企业应用情况发行版本在学习Linux前,我们可能都会问Linux从哪里来?它是如何发展的。但在介绍Linux之前,需要先介绍一下Un
- Java实现的简单双向Map,支持重复Value
superlxw1234
java双向map
关键字:Java双向Map、DualHashBidiMap
有个需求,需要根据即时修改Map结构中的Value值,比如,将Map中所有value=V1的记录改成value=V2,key保持不变。
数据量比较大,遍历Map性能太差,这就需要根据Value先找到Key,然后去修改。
即:既要根据Key找Value,又要根据Value
- PL/SQL触发器基础及例子
百合不是茶
oracle数据库触发器PL/SQL编程
触发器的简介;
触发器的定义就是说某个条件成立的时候,触发器里面所定义的语句就会被自动的执行。因此触发器不需要人为的去调用,也不能调用。触发器和过程函数类似 过程函数必须要调用,
一个表中最多只能有12个触发器类型的,触发器和过程函数相似 触发器不需要调用直接执行,
触发时间:指明触发器何时执行,该值可取:
before:表示在数据库动作之前触发
- [时空与探索]穿越时空的一些问题
comsci
问题
我们还没有进行过任何数学形式上的证明,仅仅是一个猜想.....
这个猜想就是; 任何有质量的物体(哪怕只有一微克)都不可能穿越时空,该物体强行穿越时空的时候,物体的质量会与时空粒子产生反应,物体会变成暗物质,也就是说,任何物体穿越时空会变成暗物质..(暗物质就我的理
- easy ui datagrid上移下移一行
商人shang
js上移下移easyuidatagrid
/**
* 向上移动一行
*
* @param dg
* @param row
*/
function moveupRow(dg, row) {
var datagrid = $(dg);
var index = datagrid.datagrid("getRowIndex", row);
if (isFirstRow(dg, row)) {
- Java反射
oloz
反射
本人菜鸟,今天恰好有时间,写写博客,总结复习一下java反射方面的知识,欢迎大家探讨交流学习指教
首先看看java中的Class
package demo;
public class ClassTest {
/*先了解java中的Class*/
public static void main(String[] args) {
//任何一个类都
- springMVC 使用JSR-303 Validation验证
杨白白
springmvc
JSR-303是一个数据验证的规范,但是spring并没有对其进行实现,Hibernate Validator是实现了这一规范的,通过此这个实现来讲SpringMVC对JSR-303的支持。
JSR-303的校验是基于注解的,首先要把这些注解标记在需要验证的实体类的属性上或是其对应的get方法上。
登录需要验证类
public class Login {
@NotEmpty
- log4j
香水浓
log4j
log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, HTML, DATABASE
#log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, ROLLINGFILE, HTML
#console
log4j.appender.STDOUT=org.apache.log4j.ConsoleAppender
log4
- 使用ajax和history.pushState无刷新改变页面URL
agevs
jquery框架Ajaxhtml5chrome
表现
如果你使用chrome或者firefox等浏览器访问本博客、github.com、plus.google.com等网站时,细心的你会发现页面之间的点击是通过ajax异步请求的,同时页面的URL发生了了改变。并且能够很好的支持浏览器前进和后退。
是什么有这么强大的功能呢?
HTML5里引用了新的API,history.pushState和history.replaceState,就是通过
- centos中文乱码
AILIKES
centosOSssh
一、CentOS系统访问 g.cn ,发现中文乱码。
于是用以前的方式:yum -y install fonts-chinese
CentOS系统安装后,还是不能显示中文字体。我使用 gedit 编辑源码,其中文注释也为乱码。
后来,终于找到以下方法可以解决,需要两个中文支持的包:
fonts-chinese-3.02-12.
- 触发器
baalwolf
触发器
触发器(trigger):监视某种情况,并触发某种操作。
触发器创建语法四要素:1.监视地点(table) 2.监视事件(insert/update/delete) 3.触发时间(after/before) 4.触发事件(insert/update/delete)
语法:
create trigger triggerName
after/before
- JS正则表达式的i m g
bijian1013
JavaScript正则表达式
g:表示全局(global)模式,即模式将被应用于所有字符串,而非在发现第一个匹配项时立即停止。 i:表示不区分大小写(case-insensitive)模式,即在确定匹配项时忽略模式与字符串的大小写。 m:表示
- HTML5模式和Hashbang模式
bijian1013
JavaScriptAngularJSHashbang模式HTML5模式
我们可以用$locationProvider来配置$location服务(可以采用注入的方式,就像AngularJS中其他所有东西一样)。这里provider的两个参数很有意思,介绍如下。
html5Mode
一个布尔值,标识$location服务是否运行在HTML5模式下。
ha
- [Maven学习笔记六]Maven生命周期
bit1129
maven
从mvn test的输出开始说起
当我们在user-core中执行mvn test时,执行的输出如下:
/software/devsoftware/jdk1.7.0_55/bin/java -Dmaven.home=/software/devsoftware/apache-maven-3.2.1 -Dclassworlds.conf=/software/devs
- 【Hadoop七】基于Yarn的Hadoop Map Reduce容错
bit1129
hadoop
运行于Yarn的Map Reduce作业,可能发生失败的点包括
Task Failure
Application Master Failure
Node Manager Failure
Resource Manager Failure
1. Task Failure
任务执行过程中产生的异常和JVM的意外终止会汇报给Application Master。僵死的任务也会被A
- 记一次数据推送的异常解决端口解决
ronin47
记一次数据推送的异常解决
需求:从db获取数据然后推送到B
程序开发完成,上jboss,刚开始报了很多错,逐一解决,可最后显示连接不到数据库。机房的同事说可以ping 通。
自已画了个图,逐一排除,把linux 防火墙 和 setenforce 设置最低。
service iptables stop
- 巧用视错觉-UI更有趣
brotherlamp
UIui视频ui教程ui自学ui资料
我们每个人在生活中都曾感受过视错觉(optical illusion)的魅力。
视错觉现象是双眼跟我们开的一个玩笑,而我们往往还心甘情愿地接受我们看到的假象。其实不止如此,视觉错现象的背后还有一个重要的科学原理——格式塔原理。
格式塔原理解释了人们如何以视觉方式感觉物体,以及图像的结构,视角,大小等要素是如何影响我们的视觉的。
在下面这篇文章中,我们首先会简单介绍一下格式塔原理中的基本概念,
- 线段树-poj1177-N个矩形求边长(离散化+扫描线)
bylijinnan
数据结构算法线段树
package com.ljn.base;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Set;
import java.util.TreeSet;
/**
* POJ 1177 (线段树+离散化+扫描线),题目链接为http://poj.org/problem?id=1177
- HTTP协议详解
chicony
http协议
引言
- Scala设计模式
chenchao051
设计模式scala
Scala设计模式
我的话: 在国外网站上看到一篇文章,里面详细描述了很多设计模式,并且用Java及Scala两种语言描述,清晰的让我们看到各种常规的设计模式,在Scala中是如何在语言特性层面直接支持的。基于文章很nice,我利用今天的空闲时间将其翻译,希望大家能一起学习,讨论。翻译
- 安装mysql
daizj
mysql安装
安装mysql
(1)删除linux上已经安装的mysql相关库信息。rpm -e xxxxxxx --nodeps (强制删除)
执行命令rpm -qa |grep mysql 检查是否删除干净
(2)执行命令 rpm -i MySQL-server-5.5.31-2.el
- HTTP状态码大全
dcj3sjt126com
http状态码
完整的 HTTP 1.1规范说明书来自于RFC 2616,你可以在http://www.talentdigger.cn/home/link.php?url=d3d3LnJmYy1lZGl0b3Iub3JnLw%3D%3D在线查阅。HTTP 1.1的状态码被标记为新特性,因为许多浏览器只支持 HTTP 1.0。你应只把状态码发送给支持 HTTP 1.1的客户端,支持协议版本可以通过调用request
- asihttprequest上传图片
dcj3sjt126com
ASIHTTPRequest
NSURL *url =@"yourURL";
ASIFormDataRequest*currentRequest =[ASIFormDataRequest requestWithURL:url];
[currentRequest setPostFormat:ASIMultipartFormDataPostFormat];[currentRequest se
- C语言中,关键字static的作用
e200702084
C++cC#
在C语言中,关键字static有三个明显的作用:
1)在函数体,局部的static变量。生存期为程序的整个生命周期,(它存活多长时间);作用域却在函数体内(它在什么地方能被访问(空间))。
一个被声明为静态的变量在这一函数被调用过程中维持其值不变。因为它分配在静态存储区,函数调用结束后并不释放单元,但是在其它的作用域的无法访问。当再次调用这个函数时,这个局部的静态变量还存活,而且用在它的访
- win7/8使用curl
geeksun
win7
1. WIN7/8下要使用curl,需要下载curl-7.20.0-win64-ssl-sspi.zip和Win64OpenSSL_Light-1_0_2d.exe。 下载地址:
http://curl.haxx.se/download.html 请选择不带SSL的版本,否则还需要安装SSL的支持包 2. 可以给Windows增加c
- Creating a Shared Repository; Users Sharing The Repository
hongtoushizi
git
转载自:
http://www.gitguys.com/topics/creating-a-shared-repository-users-sharing-the-repository/ Commands discussed in this section:
git init –bare
git clone
git remote
git pull
git p
- Java实现字符串反转的8种或9种方法
Josh_Persistence
异或反转递归反转二分交换反转java字符串反转栈反转
注:对于第7种使用异或的方式来实现字符串的反转,如果不太看得明白的,可以参照另一篇博客:
http://josh-persistence.iteye.com/blog/2205768
/**
*
*/
package com.wsheng.aggregator.algorithm.string;
import java.util.Stack;
/**
- 代码实现任意容量倒水问题
home198979
PHP算法倒水
形象化设计模式实战 HELLO!架构 redis命令源码解析
倒水问题:有两个杯子,一个A升,一个B升,水有无限多,现要求利用这两杯子装C
- Druid datasource
zhb8015
druid
推荐大家使用数据库连接池 DruidDataSource. http://code.alibabatech.com/wiki/display/Druid/DruidDataSource DruidDataSource经过阿里巴巴数百个应用一年多生产环境运行验证,稳定可靠。 它最重要的特点是:监控、扩展和性能。 下载和Maven配置看这里: http
- 两种启动监听器ApplicationListener和ServletContextListener
spjich
javaspring框架
引言:有时候需要在项目初始化的时候进行一系列工作,比如初始化一个线程池,初始化配置文件,初始化缓存等等,这时候就需要用到启动监听器,下面分别介绍一下两种常用的项目启动监听器
ServletContextListener
特点: 依赖于sevlet容器,需要配置web.xml
使用方法:
public class StartListener implements
- JavaScript Rounding Methods of the Math object
何不笑
JavaScriptMath
The next group of methods has to do with rounding decimal values into integers. Three methods — Math.ceil(), Math.floor(), and Math.round() — handle rounding in differen