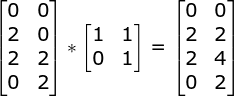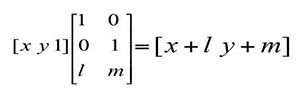css3动画的更深层次的探究（矩阵变换）

前言

其实无论哪一门技术的发展都有其根源可揪，我之前做了一些css3动画的效果，对css3流畅而又实现简单的动画效果深深着迷，遂决定探究下css3动画的来世今生，
本文如有疏漏，请各位看官及时指出，以防误导更多学习的童鞋，随着本文的深入，对看官的数学功底有一定的要求。
(更多原创请关注 小米前端博客 www.0313.name）

IE时代的Matrix滤镜

在ie浏览器大行其道的时候如果我们想实现元素的旋转与拉伸功能，那么就可以使用Matrix滤镜，他是大概长得这个模样：

filter: progid:DXImageTransform.Microsoft.Matrix( SizingMethod= sMethod ,  M11= fM11 , M12= fM12 , M21= fM21 , M22= fM22 )

先不管这个东西怎么用，但是这个应该是当时浏览器实现元素动画比较先进的方法了，那么我猜想，css3中加入的动画方法应该是借鉴了ie滤镜的实现，进一步完善和封装而成。

了解css3动画之方法

css3为我们提供了2大属性 Transform 和 animation （这个属性我会在另外一篇文章专门探究）

下面我们来看 Transform 的几个方法

其中Transform 属性主要为元素的各种变化提供了这么几个方法

移动 translate

比如我要操作一个dom位移，可以这样做：

transform:translate(30px,30px)

它表示水平方向和垂直方向同时移动30像素，当然你也可以只移动水平方向（x轴），或者垂直方向（y轴），移动的距离是相对于原来的位置，

注意，位移操作是整个css动画里面比较特殊的一种，看似简单，其实实现它可是很费劲的哦··后面会讲到

缩放 scale

对一个元素缩小一倍，可以这样做：

transform:scale(0.5)

当然你也可以放大，填入的数字大于1即可

旋转 rotate

比如我要对一个dom元素进行旋转操作，可以这样做

transform:rotate(90deg)

它表示绕元素中心顺时针旋转了90度，聪明的同学可能会问，我能不能绕指定的某一点去旋转来实现更多效果？当然可以，会用到transform-origin 指定圆心位置

扭曲 skew

对一个元素进行扭曲，可以这样做：

transform:skew(30deg，30deg)

它表示同时在水平方向(x轴)和并在垂直方向(y轴)进行扭曲变行,好吧，我知道你没听明白我说的是啥，来个图：

skew

矩阵变形 matrix

看到矩阵这个词有没有感觉到高端大气上档次，低调奢华显内涵？
没错，90%的前端程序员只会用前面几个方法，对于矩阵的使用还是很陌生
首先来看一下前面几个方法用矩阵实现的方法

#位移变换：
transform: translate(30px,30px);
transform: matrix(1, 0, 0, 1, 30, 30);

#缩放变换：
transform: scale(0.5);
transform: matrix(0.5, 0, 0, 0.5, 0, 0);

#旋转变换
transform: rotate(45deg);
transform: matrix(0.53, 0.85, -0.85, 0.53, 0, 0);//matrix(cos45',sin45',-sin45',cos45',0,0);

#扭曲变换
transform: skew(45deg);
transform: matrix(1,0,1,1,0,0);//tan45'=1;matrix(1,tan45',tan45',1,0,0)

看到前2个感觉还是很良好的吧，后2个方法是不是数学尴尬症又犯了？

总结起来，矩阵 matrix方法一共有6个参数 matrix(a, b, c, d, e, f);四个基本的变换方法都是由矩阵方法提炼而来；
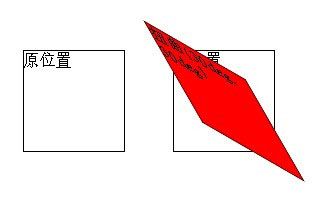
** 来一个只有矩阵才能实现的对称变换 **

matrix

(图来自 [张鑫旭的博客])

轴围绕的那个点就是CSS3中transform变换的中心点，自然，镜像对称也不例外。因为该轴永远经过原点，因此，任意对称轴都可以用y = k * x表示。则matrix表示就是：

matrix

有了公式可以直接求解了，高中的数学知识就可以求出对称的坐标，不过随后我告诉你一种更高级的方法

深入css3动画之实现

好了，进行到这里，你已经是10%中的优秀前端开发童鞋了，你尽可以在跟面试官对喷的时候放出矩阵大法，顿时会让你显得高端大气上档次，低调奢华显内涵（装b的感觉）;
说白了，你还是什么都不懂，你充其量只是会用罢了，我问你几个问题来暴漏下你的无知：

你知道为什么IE的Matrix滤镜方法不可以实现位移吗？
你知道为什么css3的矩阵 matrix会有6个参数？
你知道为什么我说css3的位移方法比较特殊吗？
你知道为什么不同的css3变换方法会对应矩阵 matrix不同的参数？是怎么算出来的吗？
你知道····为什么吗？

如果你想进一步成为1%的尖端前端人才，跟着我接着往下看（看懂了才算～～）

知识准备

矩阵的乘积

1x2维矩阵和2x2维矩阵的乘法

矩阵乘积

同理，2x2的矩阵的乘积公式是这样的，第一个矩阵第一行的x1和y1分别乘以第二个矩阵的第一列的a和c，然后其他位置参照例子可以得出；
为什么要这么算？我建议你去翻一下线性代数的第一章有详细的介绍，或是参考 阮一峰老师的对矩阵乘法的理解；
其中，（x1，y1）和（x2，y2）你可以看作是两个点坐标

矩阵乘积

在这里，我们称 第二个矩阵为 变换矩阵

几何向量

在数学中，几何向量，指具有大小（magnitude）和方向的量。向量可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。
给空间设一直角坐标系,也能把向量以数对形式表示,例如Oxy平面中(3,2)是一向量.

矩阵乘积

在这里，我们称矩阵中的一对数字(a,b)或者(c,d)为 变换向量

通过矩阵求解缩放、扭曲

假设一个方形ABCD，四个点的坐标分别为[(0,0),(2,0),(2,2),(0,2)],我要求宽放大1.5倍，高放大2倍，放大后的的方形(ABCD)'是这个样子：

坐标

那么为了得到这个变化后的方形(ABCD)'，我们直接给出变换矩阵：

坐标

看一下变换矩阵[(1.5,0),(0,2)],从字面理解一下，第一对数字（1.5,0），你可以理解为我沿着x轴将宽度延长了1.5倍，因为第二个参数是0嘛，y坐标是0，所以是沿着x轴，
那么(0,2)，道理一样，就是沿着y轴将高度延长了2倍，那么这2对数字(1.5,0)和(0,2)为 变换向量。

从严谨的数学角度来说，他们变换后的坐标是通过矩阵乘积得到的，矩阵乘积方法已经在知识准备中有交代了;

好 那么接下来 说一说扭曲，刚才讲了缩放是分别长宽沿着x轴和y轴延长，图形的基本形状没有变，还是直角，下面，我想让这个宽不再沿着x轴啦，沿着一个有角度的变换向量(1,1)来变换:

来看下变换后的坐标:

扭曲

变换后的图形的样子:

扭曲

y轴的变换向量为（0，1），你可以理解为缩放大小不变，同时没有扭曲，聪明你的是否立马能想到如何让高度也扭曲了吗？那么那你也一定知道如何让它同时缩放又扭曲

回头看一下方法：

#扭曲变换
transform: skew(45deg);
transform: matrix(1,0,1,1,0,0);//matrix(a,b,c,d,0,0)，请按照矩阵图一一对应下

所以transform: skew(45deg) 方法我们传入的是变换向量的角度值，如果用matrix方法来表示的话需要把角度值换算成三角的对边和临边的具体值；

那么缩放跟扭曲是否有一种豁然开朗的感觉？

通过矩阵求解旋转

先给出变换矩阵

旋转矩阵

比如一个点 (2,2),旋转30度，那么旋转后的坐标由下式得出：

旋转矩阵

来看下最终的方程式：

旋转矩阵

具体推导过程不再这里说了，要不然我怕童鞋们一下接受不了吐掉，这里给出一个地址感兴趣可以看下 坐标旋转推导过程

通过矩阵求解位移

终于说到这个位移了，首先我们理解下位移的实现，比如一个点（x，y）,要求分别x方向移动l个单位，y
方向移动m个单位,这个比较简单，x坐标和y坐标分别加l和m即可，新的坐标：

x`=x+l;
y`=y+m;

那么通过矩阵乘积如何得到这个公式呢？好啦，我知道这个对于一个数学恐惧症患者来说太难了，我直接给出答案：

位移

位移

这就是我卖了半天官子所要表达的意思，位移之所以特殊，为了能够使用矩阵乘积得出位移方程解我们是需要将 变换矩阵 改成 2x3维矩阵

在此，将[x y 1]称为平面坐标点[x y]的齐次坐标表示法，至于为什么要这么做呢？来博主再给你好好讲下(观众：博主你真不能再深挖了，老衲快受不了了···)

顺带解释下为什么ie的Matrix滤镜方法不能实现位移，因为它只是一个2x2的矩阵，你仔细数一下它后面需要传入的参数就知道啦

总结一下

事实上，在图形变幻中，往往需要一些比基本变换更复杂的变换，我们称由多个二维基本变换组成的复杂变换为二维组合变换

上面这句话我需要解释下，否则你会不太理解，比如，我想将一个正方形变成一个圆形，这变不了，因为不可能通过几种基本变换来达到，所以是有局限性的；

另外还有几种 基本变换 需要介绍下

第一种：图形相对于y轴的对称变化，变化矩阵为：

y轴对称

第二种：图形相对于x轴的对称变化，变化矩阵为：

x轴对称

全文高潮部分(复杂变换求解)

事实上，前面铺垫了那么多我只是为了这一部分，通过前面几节的介绍，我想童鞋们都已经 ·比较· 深刻的理解css3动画几个 基本变换 实现方式；
事实上也是基本理解，其实你还是不理解···
我来说出一下你心中的疑惑，比如位移求解方程明明简单的要死为什么非要用矩阵方式得出？这不是脱了裤子放屁（多此一举）

已经证明：任何二维组合变换均可分解为多个基本变换的乘积

只有把基本变换求解统一成矩阵求解，那么我们才能够去求解更加复杂的二维组合变换

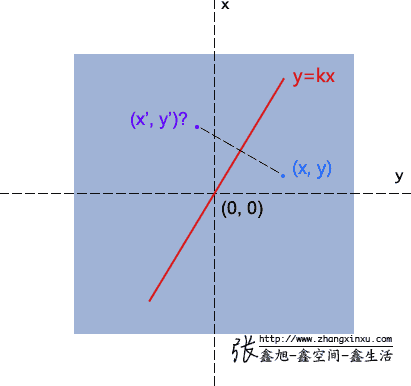
这里我们抛砖引玉，来求解下上面提到的 相对于y=kx的图形的对称变换，简单一点，假设k=1，那么就是y=x：
首先分解成基本变换：
首先让它逆时针旋转 45度，将对称方程变为 y=0，也就是求出对y轴的对称变换，然后呢，再转回去，来看一下最终的变换方程：

xy轴对称

]( http://0313.name/img/css3-animation/xytdbh.png)

其实不难看出，后面三个变换矩阵相乘结果为:

xy轴对称

所以，你也可以将y=x对称变换也可以看作是基本变换，推导过程就是我们上面的求解过程；

在将要结束的时候，我希望有同学能够通过这篇文章的学习，推导出 y=kx对称变换的求解过程，方法已经讲的很明白了···给我留言吧！

观后思考

如何求解对于一条任意直线的 Ax+By+C=0的对称变换？说一下他的求解变换过程把！

任意直线对称变换