本文翻译自2018年最热门的Python金融教程 Python For Finance: Algorithmic Trading。
本教程由以下五部分内容构成:
- Python金融入门
- 常见的金融分析方法
- 简单的动量策略开发
- 回溯测试策略
- 评估交易策略
本文是该教程的第三部分。
既然你已对数据做了初步分析,那么是时候创建你的第一个交易策略了。但在深入研究之前,为什么不先来了解一些最常用的交易策略呢?下面简短的介绍,无疑会让你更容易开始交易策略的开发。
常见的交易策略
你应该还记得在本教程开篇的介绍中,我们讲了交易策略是在市场上做多或做空的既定计划,但不仅限于此,你还有更多的信息没有真正掌握。一般来说,有两种常见的交易策略:动量策略(momentum strategy)和回归策略(reversion strategy)。
第一种是动量策略,也被称为背离(divergence)或趋势(trend)交易。当遵循该策略时,你相信数值会沿着当前的方向继续移动。也就是说你相信股票具有惯性,即有上升或下降的趋势,能被你发现并利用。
这一策略的实例包括移动均线交叉策略(moving average crossover)、双均线交叉策略(dual moving average crossover)和海龟交易策略(turtle trading)。
- 移动均线交叉是指资产的价格从移动均线的一侧移动到了另一侧。这一交叉代表了动量的改变,可以作为进入或退出市场的决策点。在本教程的后面你会学到量化交易中使用该策略的入门级案例。
- 双均线交叉发生在短期均线与长期均线交叉处。这一信号被用来识别在短期均线上的变化。买入信号发生在短期均线从下方上升超越长期均线时,而卖出信号则由短期均线从上方下降越过长期均线而触发。
- 海龟交易是一个众所周知的趋势跟踪策略,最初是由理查德·丹尼斯教授给大家的。它的基本策略是以20天高点买入期货,并在20天低点卖出。
第二种是回归策略,也被称为收敛(convergence)或循环(cycle)交易。这一策略相信数值的运动最终会逆转。这可能有点抽象,让我们来举个例子。在均值回归策略(mean reversion strategy)中,你确信股价会回到它的均值,当它偏离均值时就可以利用这一点来做决策。
听起来已经很实用了,对吧?
除了均值回归策略以外,另一个例子是与之相似的配对交易均值回归(pairs trading mean-reversion)。均值回归策略的基本思想是股价会回到其均值,而配对交易策略对此进行了扩展,认为如果能识别出两只高度相关的股票,当其中之一偏离了与另一方的相关性,两者价格差的改变就能作为交易的信号。这意味着如果这两只股票的相关性下降,那么可以做空价格较高的股票。高价格的股票最终会回到其均值,所以它应该被卖出。另一方面,做多低价格的股票,因为随着相关性恢复正常,其价格将会上升。
除了这两种最常用的策略,还有其他你偶尔可能会碰上的策略,比如预测策略,它试图基于某些历史因素预测股票在随后一段时间内的方向和价值。还有高频交易策略(HFT),它利用了亚毫秒市场的微观结构来做决策。
这都是今后的乐章了,现在让我们聚焦于开发你的第一个交易策略。
一个简单的交易策略
正如上面所述,你将从量化交易的“hello world”:移动均线交叉策略开始。你将要开发的策略很简单:对时间序列创建两个独立的简单移动均值(Simple Moving Averages, SMA),它们具有不同的回望周期,比如40天和100天。如果短期移动均值超过了长期移动均值,那么就做多;如果长期移动均值超过了短期移动均值,那么就退出。
记住当做多时,你认为股价会上涨,并且将来会以更高的价格卖出(=买入信号);当卖空时,你卖出你的股票,希望将来以更低的价格买回并实现盈利(=卖出信号)。
当你刚开始的时候,这一简单的策略可能看起来相当复杂。但是让我们一步一步来:
- 首先,定义两个不同的回望周期:一个短期窗口和一个长期窗口。设置两个变量,并对每一个变量赋值一个整数。一定要让短期窗口的值小于长期窗口的值。
- 接着,创建一个空的数据框
signals,并确保复制了aapl数据的索引,以便能开始计算aapl数据每日的买卖信号。
- 在空的
signals数据框中创建一列名为signal的数据,并将其每一行的数值初始化为0.0。
- 做好了准备工作后,是时候在各自的时间窗口上创建短期和长期的简单移动均值了。使用
rolling()函数开始滑动窗口计算:在该函数中,设置window、min_period和center参数。在实际中,窗口大小window分别设置为short_window和long_window。min_period设为1,作为窗口中观测量的最小值。center的值为False,这样标签就不会设置在窗口的中心。接着,不要忘了在其后连接mean()函数以便能计算滚动均值。
- 当计算了短期和长期窗口的均值后,你应该在短期移动均线与长期移动均线交叉处创建信号,但这仅针对大于最短移动均值窗口的时期。在Python中,这对应着如下条件不等式:
signals['short_mavg'][short_window:] > signals['long_mavg'][short_window:]。注意加上[short_window:]是为了遵守条件“仅针对大于最短移动均值窗口的时期”。当上述条件不等式为真时,signal列中的初值0.0将被替换为1.0。 这样一个“信号”就产生了。如果条件不等式为假,将继续保留原始值0.0,也没有信号产生。使用 NumPy 中的where()函数来设置这一条件不等式。就像你刚才读到的那样,将这一结果赋值给变量signals['signal'][short_window],因为我们仅想针对大于最短移动均值窗口的时期创建信号。
- 最后,计算信号的差值,从而生成实际的交易订单。换句话说,在
signals数据框的positions这一列中,你将能区分多头和空头头寸,无论是买入或卖出股票。
尝试下方的代码:
# 导入apple公司股票数据
import pandas_datareader as pdr
import datetime
aapl = pdr.get_data_yahoo('AAPL',
start=datetime.datetime(2006, 10, 1),
end=datetime.datetime(2012, 1, 1))
# 导入pandas,numpy
import pandas as pd
import numpy as np
# 初始化短期和长期窗口
short_window = 40
long_window = 100
# 初始化 `signals` 数据框,增加 `signal` 列
signals = pd.DataFrame(index=aapl.index)
signals['signal'] = 0.0
# 创建短期简单移动均值
signals['short_mavg'] = aapl['Close'].rolling(window=short_window, min_periods=1, center=False).mean()
# 创建长期简单移动均值
signals['long_mavg'] = aapl['Close'].rolling(window=long_window, min_periods=1, center=False).mean()
# 生成信号
signals['signal'][short_window:] = np.where(signals['short_mavg'][short_window:]
> signals['long_mavg'][short_window:], 1.0, 0.0)
# 生成交易命令
signals['positions'] = signals['signal'].diff()
# 输出`signals`
print(signals)
signal short_mavg long_mavg positions
Date
2006-10-02 0.0 10.694285 10.694285 NaN
2006-10-03 0.0 10.638571 10.638571 0.0
2006-10-04 0.0 10.681905 10.681905 0.0
2006-10-05 0.0 10.683928 10.683928 0.0
2006-10-06 0.0 10.667714 10.667714 0.0
2006-10-09 0.0 10.666667 10.666667 0.0
2006-10-10 0.0 10.649184 10.649184 0.0
2006-10-11 0.0 10.625714 10.625714 0.0
2006-10-12 0.0 10.639683 10.639683 0.0
2006-10-13 0.0 10.647429 10.647429 0.0
2006-10-16 0.0 10.658701 10.658701 0.0
2006-10-17 0.0 10.654881 10.654881 0.0
2006-10-18 0.0 10.654286 10.654286 0.0
2006-10-19 0.0 10.699286 10.699286 0.0
2006-10-20 0.0 10.747429 10.747429 0.0
2006-10-23 0.0 10.803036 10.803036 0.0
2006-10-24 0.0 10.848655 10.848655 0.0
2006-10-25 0.0 10.894206 10.894206 0.0
2006-10-26 0.0 10.938797 10.938797 0.0
2006-10-27 0.0 10.966214 10.966214 0.0
2006-10-30 0.0 10.991088 10.991088 0.0
2006-10-31 0.0 11.017987 11.017987 0.0
2006-11-01 0.0 11.030621 11.030621 0.0
2006-11-02 0.0 11.041131 11.041131 0.0
2006-11-03 0.0 11.046857 11.046857 0.0
2006-11-06 0.0 11.059945 11.059945 0.0
2006-11-07 0.0 11.076296 11.076296 0.0
2006-11-08 0.0 11.101378 11.101378 0.0
2006-11-09 0.0 11.129113 11.129113 0.0
2006-11-10 0.0 11.153952 11.153952 0.0
... ... ... ... ...
2011-11-17 1.0 56.485857 54.946829 0.0
2011-11-18 1.0 56.381000 55.005257 0.0
2011-11-21 1.0 56.259000 55.052886 0.0
2011-11-22 1.0 56.177750 55.100386 0.0
2011-11-23 1.0 56.070536 55.125471 0.0
2011-11-25 1.0 55.974107 55.142343 0.0
2011-11-28 1.0 55.955536 55.169371 0.0
2011-11-29 1.0 55.950536 55.188643 0.0
2011-11-30 1.0 55.985179 55.228929 0.0
2011-12-01 1.0 56.019750 55.277757 0.0
2011-12-02 1.0 56.063786 55.323014 0.0
2011-12-05 1.0 56.146679 55.373357 0.0
2011-12-06 1.0 56.154322 55.410543 0.0
2011-12-07 1.0 56.114322 55.432386 0.0
2011-12-08 1.0 56.073143 55.452114 0.0
2011-12-09 1.0 56.020250 55.461714 0.0
2011-12-12 1.0 55.912536 55.468214 0.0
2011-12-13 1.0 55.801179 55.461800 0.0
2011-12-14 1.0 55.651000 55.435643 0.0
2011-12-15 1.0 55.580715 55.400686 0.0
2011-12-16 1.0 55.529679 55.384157 0.0
2011-12-19 1.0 55.491607 55.370429 0.0
2011-12-20 1.0 55.456536 55.378243 0.0
2011-12-21 1.0 55.451822 55.377814 0.0
2011-12-22 1.0 55.444500 55.391586 0.0
2011-12-23 1.0 55.439643 55.406957 0.0
2011-12-27 0.0 55.445286 55.448614 -1.0
2011-12-28 0.0 55.437643 55.490072 0.0
2011-12-29 0.0 55.468393 55.564229 0.0
2011-12-30 0.0 55.495500 55.608500 0.0
[1323 rows x 4 columns]
不是很难,对吧?输出 signals 数据框并检查其结果。这里重要的是要掌握该数据框中 positions 和 signal 这两列的含义。当你继续下去时,会发现这一点变得非常重要。
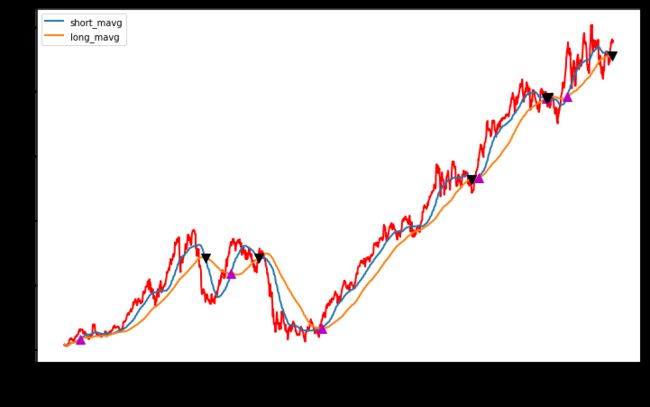
当你花时间去理解该交易策略的结果时,可以用 Matplotlib 将短期和长期的移动均线,以及买入和卖出的信号,快速绘制在图中。
# 导入`pyplot` 模块
import matplotlib.pyplot as plt
# 初始化图形
fig = plt.figure(figsize=(12,8))
# 增加子图并设置y轴标签
ax1 = fig.add_subplot(111, ylabel='Price in $')
# 绘制收盘价曲线
aapl['Close'].plot(ax=ax1, color='r', lw=2.)
# 绘制短期和长期移动均线
signals[['short_mavg', 'long_mavg']].plot(ax=ax1, lw=2.)
# 绘制买入信号
ax1.plot(signals.loc[signals.positions == 1.0].index,
signals.short_mavg[signals.positions == 1.0],
'^', markersize=10, color='m')
# 绘制卖出信号
ax1.plot(signals.loc[signals.positions == -1.0].index,
signals.short_mavg[signals.positions == -1.0],
'v', markersize=10, color='k')
# 显示做图
plt.show()
结果很酷,不是吗?