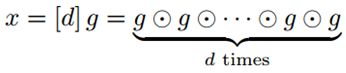15级网络工程6班 赵雪婷 20152100213
阅读Martin Eker˚a ,Johan H˚astad在17年二月份发表的Quantum algorithms for computing short discrete logarithms and factoring RSA integers的文章,有所收获。
文章基于量子计算机上主要描述了计算短离散对数的量子算法和分解RSA大整数量子算法。
一、归纳文章主要思想与工作:
计算机通常被认为是一个通用的计算设备;即,它被认为能够在至多一个多项式系数计算时间成本模拟任何物理计算设备:目前尚不清楚这是否是真的在考虑量子力学。一些研究人员,从David Deutsch开始,已经发展了量子力学的计算机模型,研究了它们的计算性能。本文给出了拉斯维加斯算法寻找因数分解和离散对数的整数的量子计算机上,采取一系列步骤中输入的大小,是多项式如被分解的整数位数。这两个问题通常被认为是难在经典计算机上已使用的几个提议的密码系统为基础。因此我们给出量子密码分析的第一个例子。
在本文中,我们概括为计算短的离散对数先前推出的以{ \\ AA }以便为次,算法需要一方面执行的数量不同的权衡之间的量子算法,以及算法的复杂性,要求它对另一方面量子计算机。此外,我们还描述了计算短离散对数的算法的应用。特别是,我们展示了其他重要的问题,如分解RSA整数和寻找边信息下的群的次序的问题,可以改写为短离散对数问题。这立即引起一个算法分解RSA的整数比短的一般分解算法在某种意义上说,它对较小的要求对量子计算机那么复杂。在我们的算法和Shor算法,主要的障碍是计算叠加模幂运算。当保理n位整数,指数是长度在Shor算法2n位,相比略超过n / 2位在我们的算法。
二、讨论相关技术:
量子计算算法:
量子计算机利用量子力学原理进行计算,具有量子并行计算的优势,能够超越经典计算1990年中期,量子算法取得突破,舒尔(Shor)构造了大数质因子的量子算法,葛洛沃(Grover)构造了无序数据库的量子搜索算法,引起了人们对量子计算的重视,极大地推动了量子计算的研究.文章简单介绍了几个典型的量子算法以及量子算法研究的一些新进展.
离散对数:
是在整数中,一种基于同余运算和原根的一种对数运算:当模m有原根时,设L为模m的一个原根,则当?x≡L^k(mod m)时: IndLx≡?k (mod Φ(m)),此处的IndLx为 x以整数L为底,模Φ(m)时的离散对数值。或者简单描述离散对数问题为:给定一个质数p,和有限域Zp上的一个本原元a,对Zp上整数b,寻找唯一的整数c,使得a^c≡b(mod p)。一般的,如果仔细选择p,则认为该问题是难解的,且目前还没有找到计算离散对数问题的多项式时间算法。为了抵抗已知的攻击,p至少应该是150位的十进制整数,且p-1至少有一个大的素数因子。
离散对数公钥加密算法是目前最为热门的公钥加密算法 ,其安全性要远远高于基于大数分解的RSA算法。
首先说明一下上述三位科学家公钥密码体制的运作过程(假定A和B两个人要在一个不安全通道如因特网上形成密钥以备日后加密解密所用)。
首先,A、B两人要共同公开约定一个素数q和有限域Fq中的一个生成元g;
A选定一个随机数a∈{1,2,…,q-1}(a可以认为是A之私钥),并将g a(modq)传送给B;
B选定一个随机数b∈{1,2,…,q-1}(b可以认为是B之私钥),并将gb(modq)传送给A;
此时A可以算出(g b)a(modq),B也可以算出(g a)b(modq),由于(gb)a(modq) = (g a)b(modq) = g ab(modq),因此,A和B就形成了一个公共的密钥g ab(modq),日后便可以此钥来进行传统的加密解密计算,从而达到在不安全的通道上进行保密通讯的目的。
显然,敌方可以截获到g,q,g a(modq),g b(modq)。因此,如果敌方有快速的求解离散对数的算法,就能从已截获的上述信息中迅速求出a或b,从而算出g ab(modq)。遗憾的是,目前世界上根本就没有快速的求解离散对数的算法,因此当所选的有限域Fq很大时,a或b就很难算出。
3.量子计算机:
量子计算机(quantum computer)是一类遵循量子力学规律进行高速数学和逻辑运算、存储及处理量子信息的物理装置。当某个装置处理和计算的是量子信息,运行的是量子算法时,它就是量子计算机。量子计算机的概念源于对可逆计算机的研究。研究可逆计算机的目的是为了解决计算机中的能耗问题。
4.RSA数分解:
RSA算法是一种用数论构造的、被认为理论上相当成熟的公钥密码体制,并广泛地应用于密钥管理、数字签名等方面。基于数论中2个大素数乘积所得整数n和选取满足一定条件的整数e组成公开密钥(e, n),并选取特定私钥d组成私有密钥对(d, n)。RSA算法的安全性是基于数论中大整数分解的困难性。对RSA加密体制的攻击来自多方面,主要有因式分解和旁路攻击方法等,而对加密算法的攻击是检验算法安全性的标志。在对n的因式分解方法中,在给定e和n的情况下,确定d的计算量至少等价于整数分解问题。目前,比较常用的因式分解方法有试除法、Fermat分解法、Pollard’s rho分解法、Pollard’s P-1分解法、Dixon分解法、连分数分解法、二次筛法、多多项式二次筛法、数域筛法(NFS)和椭圆曲线分解法等。其中,数域筛法被认为是当前最有效的大数分解算法。在这些算法中,大多是基于求同余式
22(mod)xyn≡且(mod)xyn≠±所构成的完全平方数x和y,只要求出x和y,即可通过求gcd(x+y, n)和gcd(x–y, n)达到分
解n的目的。它们的分解效率取决于构造的算法技巧。而随着密钥n增大到1 024位以上,分解难度大大地增大。
(一)量子计算
量子计算是一种遵循量子力学规律调控量子信息单元进行计算的新型计算模式。对照于传统的通用计算机,其理论模型是通用图灵机;通用的量子计算机,其理论模型是用量子力学规律重新诠释的通用图灵机。从可计算的问题来看,量子计算机只能解决传统计算机所能解决的问题,但是从计算的效率上,由于量子力学叠加性的存在,目前某些已知的量子算法在处理问题时速度要快于传统的通用计算机。
1)首先,先了解量子系统。每个状态位用|j>表示(0≤ j< 2n),状态的叠加即为量子系统。系统表达式函数如下:
(其中复振幅
aj ∈ R是一个非负实波,相位
)故而,系统表达函数亦可表示为:
2)通过建设性干预手段,离散量子傅里叶变换算法(QFT)放大一系列所需要的状态的幅度,所需状态的的折叠概率会增大。如果量子比特形成了最大程度的纠缠,他们的波函数坍缩结果就完全相关。
QFT将每个状态映射到n个量子位寄存器中
所以,QFT映射下的量子系统函数为
系统叠加到k的概率为
在和的运算中术语用向量C表示。如果向量C几乎指向相同一个方向,那么它们的规范总和有很大可能概率。那么我们就说,对于k,建立了建设性干预。
主张一:
(二)计算短离散对数
计算离散对数可用于攻击一些非对称加密算法,例如DH加密,选择和比较非对称密码参数。计算短离散对数的生成算法包括两个阶段:初始化量子阶段和经典后处理阶段。
初始化量子阶段:输入生成元g和x = [d] g得到一对(j,k)。
经典后处理阶段:用一个经典的算法来描述,基于lattice-based技术,经典算法输入一系列s对(j,k),计算输出d。
具体算法如下:
令:
int d(0
固定int s>=1;
int l close to m/s;
g为阶数r>=2^(l+m)+2^ld的一个有限循环群的生成元;
g叠加到长度为l + m位的指数上的指数运算
input g,x = [d] g;
output (j,k);
when s>=1
calculate (j,k);
return d。
(解决离散对数问题d = log g x)
Tips1
良好对的定义:
当j为整数(0<=j<2^(l+m)),如果
(j决定k,dj mod 2^(l+m),最高阶为l)
至少有2^(l+m-1)个不同的j,才会有一个k,使得(j,k)为良好对。
Tips2
为了降低产生一个良好对的概率,我们首先需要对(a,b)数量的下界产生具体确定的e
定义:Te表示对(a,b)的数量,e=a-bd
(其中,a,b均为整数并且0<=a<2^(l+m),0<=b<2^l)
文章主张二:
文章主张三:
文章主张四:
从算法的单个执行中,获得特别良好对(j,k)的概率至少为2^(-m-l-2)
算法单次运行结果产生一副良好对的概率至少为2^(-3)
Tips3
基于lattice-based技术,经典算法输入一系列s对(j,k),计算输出d
Lattice格子定义:(L由下列行跨度产生的整数)
(三)分解大整数
首先,我们通过将分解因式的问题作为解短离散对数问题对待,来获得两个因子。一个方法就是N近似φ(N),这使得我们解决短的离散对数问题时不需要事先知道顺序。其次,我们通过执行量子算法产生一系列的部分结果来获得两个因素。我们可以基于lattice-based技术在经典后期处理中恢复离散对数d。它从产生的一系列部分结果中构造格L和向量v,通过L趋近于V恢复d。
具体算法如下:
任意素数p,q(p>2^(n-1),q<2^n);
N=p*q;
φ(N)=(p-1)(q-1);
t>=gcd(p-1,q-1);
φ(N)/t>(p+q-2)/2;
G的生成元为g(1
根据g和x计算短离散对数d=(p+q-2)/2;
when(0
m=n+1;
阶数φ(N)/t>=2^(l+m+1));
if s>=1,l=m/s=(n+1)/s;
t<2^(n-l-4)概率很高;
φ(N)=(p-1)(q-1)>=2^(2(n-1))'
N=(2d-q+2)q (其中2d+2=p+q)
if c=d+1,
return p,q;
四、指出未来的研究方向、未解决的难题等:
自上世纪20年代以来,随着薛定谔、爱因斯坦、海森伯格、狄拉克等人所建立起的量子力学不断发展,以及实验水平的不断提高,人们对于量子力学有了更加深刻但仍不完善的理解与认知。量子计算机,作为站在巨人肩膀上的产物,因其强大的并行计算能力,受到各国政府、学者、企业的重视和追逐,也正是因此,量子计算机的发展势如破竹。
就现阶段而言,量子计算机的发展方向即为从理论阶段转为可使用的状态。随着目前各国实业界巨擘如Google、微软的巨额投入,以及学术界、政府部门的鼎力支持,未来10年内实现“小”而可用的量子计算机指日可待。