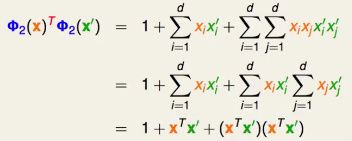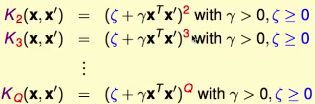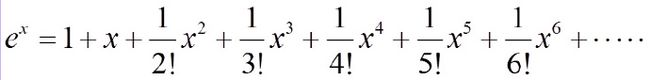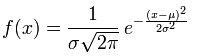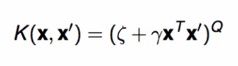机器学习技法--Kernel SVM

本文参考整理了Coursera上由NTU的林轩田讲授的《机器学习技法》课程的第三章的内容，主要介绍了Kernel SVM和核函数Kernel Function的基本概念及理论，主要介绍了Polynomial Kernal、Gaussian Kernel等内容，文中的图片都是截取自在线课程的讲义。
欢迎到我的博客跟踪最新的内容变化。
如果有任何错误或者建议，欢迎指出，感激不尽！
--

本系列文章已发三章，前两章的地址如下：

一、线性SVM
二、SVM的对偶问题

经过上一章的推导，我们的SVM对偶问题已经是这个形式了

这个问题的瓶颈在于矩阵Q的计算，而q(n,m)=ynymZn’*Zm，需要计算R(d_{)空间内的两个向量的内积，并没有摆脱d}的依赖。

问题：我们如何才能快速计算Zn’Zm=Φ(Xn)’Φ(Xm)呢？如何才能比O(d~)快呢？

从Z空间的角度看，这就是两个d_{维向量的内积，不可能快于O(d})。
但如果从原始的X空间来看，这一步其实是两步：我们首先把原始资料(Xn,yn)通过转换Φ映射到空间Z，再计算内积。
如果我们能直接在X空间内完成这两步，应该可以快于O(d~)。

Kernel Trick

简单的例子

首先考虑一个简单的二次多项式转换Φ2，设原始X空间的维度是d，即原始资料有d个特征。

注意：为了简单起见，该转换函数同时包含了相同的x1*x2和x2*x1

我们尝试推导直接在X空间内完成以上两步(映射、内积)所对应的函数是怎么样的

我们在X空间内任意选取两个特征向量X和X’

发现Z空间内的内积，可以由X空间内的内积表达出来。

这样我们不用先花O(d^{2)的力气进行转换，再花O(d}2)的力气进行内积计算，我们可以直接先花O(d)的力气算出在X空间内的内积，在计算中再把它平方就好了，这样花费的时间不过是O(d)的复杂度。

我们把这个“转换”和“内积”合二为一的函数叫做核函数(kernel function)，所以某个特征转换就对应到某个kernel function，我们希望kernel function比较容易计算。

有了kernel function后，我们可以把求解SVM的对偶问题时，需要计算Zn’Zm的地方都换成kernel function表示的形式。

注意W可以由ynZn的α线性组合得到，W’Z同样包含Zn’Z，因此也可以利用kernel function快速计算。

这种技巧就叫做kernel trick，它的核心是通过利用一个X空间内的计算高效的kernel function的计算，来映射到经过特征转换到Z空间后的两个向量的内积结果。
由于核函数的计算是在X空间内完成的，它就避免了对Z空间的高维度d~的依赖。

Kernel Hard-Margin SVM Algorithm

我们称这种利用了kernel trick进行高维度特征转换的SVM为kernel SVM，它的一般求解过程如下：

它的时间复杂度

计算NN的矩阵Q，时间复杂度是O(N^2)O(kernel function)
QP求解，只有N个变量，N+1个条件
& 4. O(#SV)*O(kernel function) [#SV代表SV的数量]

因此，只要kernel function的求解和d_{无关，可以很快算出来，那么以上步骤就可以很快地、和d}无关地计算出来。

所以，kernel SVM本质上就是把原来SVM的瓶颈部分，利用了核函数这种计算上的便捷方法，从而避免了对d~的依赖的一种SVM，它同样只需要支撑向量SV点就可以进行新数据的预测。

多项式核

上一节中作为例子的二次多项式转换并不是唯一的二次多项式转换，下面介绍一些常用的多项式转换及其对应的核函数。

如果我们把所有的一次项都放缩√2倍，则

如果我们把二次项和一次项再一并进行γ倍的放缩，则

即

这样经过适当放缩后的多项式转换的核函数，其数学表达形式看起来更加整洁一点，这是大家平常比较常用的一种形式，也比较容易延伸到更高次方的多项式。

其实放缩前的蓝色的Φ2和放缩后的绿色的Φ2的特征转换空间的能力是一样的，它的缩放系数最终会被线性函数的W中的元素的放缩所包含，但它们确实是不同的转换，最终算出来的形式不一样，是因为它们定义了不同的内积，在内积空间中，不同的内积，就代表不同的距离，不同的距离就有不同的几何特性，对于SVM算出的Margin就不一样，就可能会得到不同的边界。

因为绿色的Φ2比较简单，我们一般直接把它叫做K2，相对比较常用。

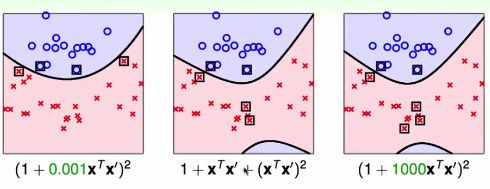
不同kernel的几何表现

因此不同的二次多项式转换，g(svm)可能不同，支撑向量SVs也不同。

在学习之前，很难说究竟哪一个更好。

因此，kernel的改变，同时就意味着margin距离的几何定义的改变。

我们需要选择kernel，就像之前对转换Φ做选择，因为转换现在已经包含在kernel里面了。

常用一般多项式核

对于原来的K2，我们还可以加一个自由度ζ，来表示常数项的放缩。

对应的转换为

推广到3次方、4次方......Q次方

我们将转换ΦQ嵌入到（γ，ζ）这些参数的选择中，这样就允许我们计算非常高次的多项式转换的空间中的large-margin问题，该问题不再依赖于转换空间的维度d~。

SVM + 多项式核 = 多项式SVM

注意：有时候转换比较简单时，直接求解原始的SVM问题反而更加简单有效，而不必利用kernel求解SVM的对偶问题，比如linear kernel K1，我们之前说过，应该首先尝试简单的线性模型。

高斯核

我们之前使用kernel function来将到Z空间的转换和内积合成一步，形成了一个X空间内的函数，从而节省了力气，如果我们能够找到一个映射到无限多维的Z空间的核函数，是不是意味着我们可以使用无限多维的转换呢？

一维特征

我们先考虑简单情况，假设输入特征只有一个维度，即X=(x)，我们考虑一个特别的函数K(x,x’)

注意第三步用到了泰勒公式在0点处的展开，即麦克劳林展开，e^x的麦克劳林展开如下：

根据泰勒公式

这样我们就得到K(x,x’)就是经过这个无限多维转换Φ(x)的核函数。

一般的高斯核

更一般地，X有多个维度，有γ放缩的高斯函数都可以这样表达核函数

RBF核

我们来观察一下Gaussian SVM的Hypothesis是什么形式

不难发现g(svm)是很多中心在支撑向量SV Xn 上面的高斯函数的线性组合。
因此，很多人也把高斯核叫做Radial Basis Function (辐射状(类似高斯函数的形状)的基函数(用来作线性组合的函数) Kernel，即RBF Kernel。

因此，Gaussian SVM就是找到对中心在Xn上的高斯函数进行线性组合的系数αn，并满足在无限多维空间里面最大margin的要求。

高斯SVM的几何表现

γ变大，相当于高斯函数的标准差σ变小，Gaussians就变得尖了，线性组合后曲线就会不均匀，变得不平滑甚至产生孤岛。

虽然有large margin的保证可以尽量避免overfit，但如果γ选取的不好(过大)，还是可能overfit。

因此，使用Gaussian SVM时候，要慎重选择参数γ，通常不建议使用太大的γ。

无限大的γ

如果γ->∞，那么K(x,x')=exp(-γ|x-x'|^2)会趋向于什么呢？

如果x=x'，则不论γ为多少，K(x,x')=1。
如果x!=x'，则当γ->∞时，K(x,x')->0。

因此K(limit)好像是一个脉冲函数，它是当γ趋向于∞时，高斯函数变得尖尖的极端情况。

因此K(limit)=[[ x=x' ]] ，[[ ]]表示布尔运算。

不同Kernel的优缺点

linear kernel

优点：

简单、安全，应该首先尝试
有专门针对primal问题设计的QP Solver，比较快，没必要解对偶问题
模型可解释性好，W和支撑向量SV可以告诉我们模型认为哪些feature或者data point是重要的。

缺点：

应用场所有限，如果数据不是线性可分，就不可用

Polynomial Kernel

优点：

比linear的应用限制更少，可以解决non-linear separable的数据
可以通过Q很强地控制模型的物理意义，比如你知道数据的关系是几次方，则可以直接通过Q来表达这种信息。

缺点：

kernel function的计算在数值上有困难，当Q变大时

* 如果|ξ+γX’X'|<1，则K->0
* 如果|ξ+γX’X'|>1，则K->big

有三个参数(γ,ξ,Q)需要选择，选择上比较困难

因此，Polynomial Kernel通常只会用在你已经大概知道要用的Q是多少，且Q不是很大。
有时，当Q比较小时，直接把Z空间展开，解primal SVM也很有效率。

Gaussian Kernel

优点：

比linear/poly都更加powerful
kernel function的范围在[0,1]，因此数值计算上的困难度比poly要低
只有一个参数γ需要选择，比poly在参数选择上更加简单

缺点：

比较难于解释--没有计算出来W
比linear要更慢
过于powerful，容易overfit

Gaussian Kernel是最常用的SVM Kernel之一，但是使用时要小心选择参数。

其他合理的Kernels

Kernel代表什么？

Kernel代表内积，其实就是代表Z空间内的两个向量Φ(x)和Φ(x’)的相似性，因此我们可以直接从相似性衡量的效果出发，定义出自己的Kernel。

但并不是所有相似性衡量都可以是Kernel，需要数学上证明。

Mercer's Condition

Valid Kernel的必要条件：

对称矩阵，因为向量内积是对称的
考虑矩阵K，其中Kij=K(Xi,Xj)

K = Z*Z’，是两个Z矩阵的相乘，根据线性代数的理论，K一定是半正定(positive semi-definite)的。

以上两个条件，被数学家证明还是充分条件，这两个条件是否满足就代表着你定义的kernel function是否合法，这两个条件就叫做Mercer's Condition。

定义自己的kernel虽然可能，但是很难。

我们目前从SVM的Primal问题推导到了Kernel，但是还没有解决如果Z空间内的数据点不是linear-separable的问题，我们坚持所有的OO和XX必须用一个超平面完美分割，这样可能会造成问题，比如模型可能去fit Noise等等，容易过拟合，我们能否把像Gaussian SVM里面的这种overfitting的情形再用一些方式控制解决，这需要将目前的Hard Margin改为Soft Margin，允许一些点可以出错，我们将在下一章探讨Soft Margin SVM的问题。

Mind Map Summary

有关Soft-Margin SVM及更多机器学习算法相关的内容将在日后的几篇文章中分别给出，敬请关注！