面试算法：二叉树的Morris遍历算法

如果你喜欢编译原理，请参看视频
用java开发C语言编译器

如果你喜欢面试算法，请参看视频
如何进入google,算法面试技能全面提升指南

如果你对机器学习感兴趣，请参看一下链接：
机器学习：神经网络导论

如果你喜欢操作系统内核，请参看视频
Linux kernel Hacker, 从零构建自己的内核

对二叉树节点的遍历一般来说有中序，后序，和前序三种遍历方法，如果二叉树的高用h来表示，那三种遍历方法所需要的空间复杂度为O(h). 例如对于中序遍历来说，如果我们使用递归来实现的话，代码如下：

void inorderTraval(TreeNode root) {
    if (root == null) {
        return;
    }

    inorderTraval(root.left);
    System.out.print(root.value + " ");
    inorderTraval(root.right);
}

上面的实现中，有函数的递归调用，递归的深度等于二叉树的高度，也就是说递归导致的调用堆栈的高度等于二叉树的高度，这样的话，程序虽然没有显示的通过new 来分配内存，但实际上消耗的内存大小也是 O(h). 如果二叉树的高度很大，例如搜索引擎把几十亿张网页按照权重来组成二叉树的话，那么二叉树的高度也要几十万作用，因此按照传统的中序遍历，需要消耗大量的内存。

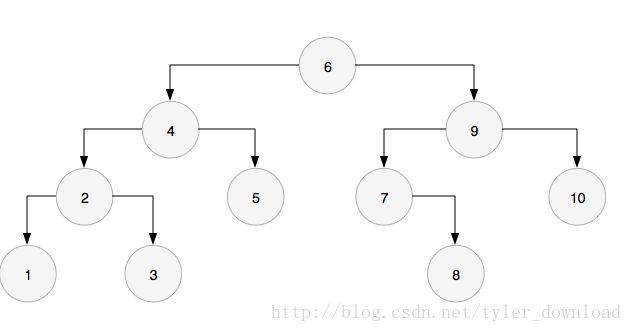
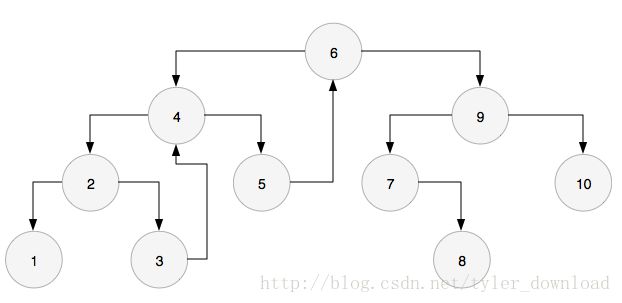
本节要讲的Morris遍历法，能以O(1)的空间复杂度实现二叉树的中序遍历。例如给定下面二叉树：

这里写图片描述

采用中序遍历的话，二叉树节点的访问情况如下：

1，2，3，4，5，6，7，8，9，10

给定某个节点，在中序遍历中，直接排在它前面的节点，我们称之为该节点的前序节点，例如节点5的前序节点就是4，同理，节点10的前序节点就是9.

在二叉树中如何查找一个节点的前序节点呢？如果该节点有左孩子，那么从左孩子开始，沿着右孩子指针一直想有走到底，得到的节点就是它的前序节点，例如节点6的左孩子是4，沿着节点4的右指针走到底，那就是节点5，节点9的左孩子是7，沿着它的右指针走到底对应的节点就是8.

如果左孩子的右节点指针是空，那么左孩子就是当前节点的前序节点。

如果当前节点没有左孩子，并且它是其父节点的右孩子，那么它的前序节点就是它的父节点，例如8的前序节点是7，10的前序节点是9.

如果当前节点没有左孩子，并且它是父节点的左孩子，那么它没有前序节点，并且它自己就是首节点，例如节点1.

值得注意的是，前序节点的右指针一定是空的。

Morris遍历算法的步骤如下：

1， 根据当前节点，找到其前序节点，如果前序节点的右孩子是空，那么把前序节点的右孩子指向当前节点，然后进入当前节点的左孩子。

2， 如果当前节点的左孩子为空，打印当前节点，然后进入右孩子。

3，如果当前节点的前序节点其右孩子指向了它本身，那么把前序节点的右孩子设置为空，打印当前节点，然后进入右孩子。

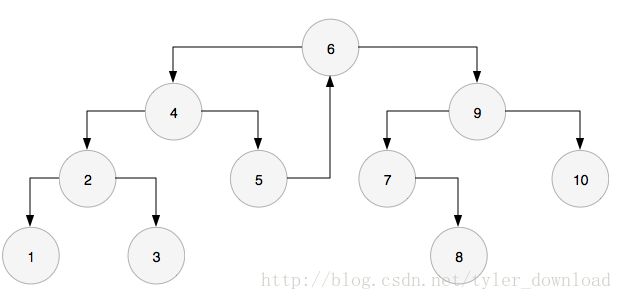
我们以上面的例子走一遍。首先访问的是根节点6，得到它的前序节点是5，此时节点5的右孩子是空，所以把节点5的右指针指向节点6：

这里写图片描述

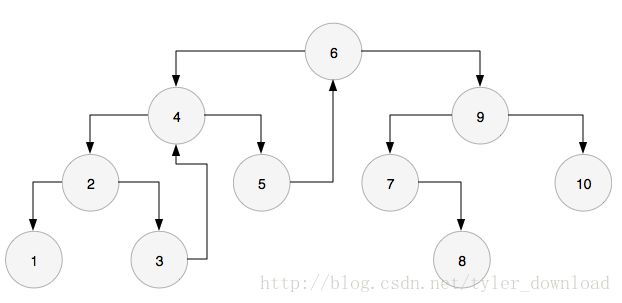
进入左孩子，也就到了节点4，此时节点3的前序节点3，右孩子指针是空，于是节点3的右孩子指针指向节点4，然后进入左孩子，也就是节点2

这里写图片描述

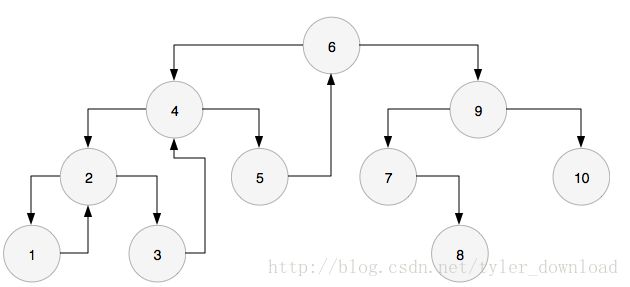
此时节点2的左孩子1没有右孩子，因此1就是2的前序节点，并且节点1的右孩子指针为空，于是把1的右孩子指针指向节点2，然后从节点2进入节点1：

这里写图片描述

此时节点1没有左孩子，因此打印它自己的值，然后进入右孩子，于是回到节点2.根据算法步骤，节点2再次找到它的前序节点1，发现前序节点1的右指针已经指向它自己了，所以打印它自己的值，同时把前序节点的右孩子指针设置为空，同时进入右孩子，也就是节点3.于是图形变为：

这里写图片描述

此时节点3没有左孩子，因此打印它自己的值，然后进入它的右孩子，也就是节点4. 到了节点4后，根据算法步骤，节点4先获得它的前序节点，也就是节点3，发现节点3的右孩子节点已经指向自己了，所以打印它自己的值，也就是4，然后把前序节点的右指针设置为空，于是图形变成：

这里写图片描述

接着从节点4进入右孩子，也就是节点5，此时节点5没有左孩子，所以直接打印它本身的值，然后进入右孩子，也就是节点6，根据算法步骤，节点6获得它的前序节点5，发现前序节点的右指针已经指向了自己，于是就打印自己的值，把前序节点的右指针设置为空，然后进入右孩子。

接下来的流程跟上面一样，就不再重复了。我们看看具体的实现代码：

public class MorrisTraval {
    private TreeNode root = null;
    public MorrisTraval(TreeNode r) {
        this.root = r;
    }
    
    public void travel() {
        TreeNode n = this.root;
        
        while (n != null) {
            if (n.left == null) {
                System.out.print(n.vaule + " ");
                n = n.right;
            } else {
                TreeNode pre = getPredecessor(n);
                
                if (pre.right == null) {
                    pre.right = n;
                    n = n.left;
                }else if (pre.right == n) {
                    pre.right = null;
                    System.out.print(n.vaule + " ");
                    n = n.right;
                }
                
            }
        }
    }
    
    private TreeNode getPredecessor(TreeNode n) {
        TreeNode pre = n;
        if (n.left != null) {
            pre = pre.left;
            while (pre.right != null && pre.right != n) {
                pre = pre.right;
            }
        }
        
        return pre;
    }
    
}

getPredecessor 作用是获得给定节点的前序节点，travel 接口做的就是前面描述的算法步骤，在while循环中，进入一个节点时，先判断节点是否有左孩子，没有的话就把节点值打印出来，有的话，先获得前序节点，然后判断前序节点的右孩子指针是否指向自己，是的话把自己的值打印出来，进入右孩子，前序孩子的右孩子指针是空的话，就把右孩子指针指向自己，然后进入左孩子。

Morris遍历，由于要把前缀节点的右指针指向自己，所以暂时会改变二叉树的结构，但在从前缀节点返回到自身时，算法会把前缀节点的右指针重新设置为空，所以二叉树在结构改变后，又会更改回来。

在遍历过程中，每个节点最多会被访问两次，一次是从父节点到当前节点，第二次是从前缀节点的右孩子指针返回当前节点，所以Morris遍历算法的复杂度是O(n)。在遍历过程中，没有申请新内存，因此算法的空间复杂度是O(1).

更多技术信息，包括操作系统，编译器，面试算法，机器学习，人工智能，请关照我的公众号：

这里写图片描述