嵌入式团队培训_线性结构
嵌入式团队培训_线性结构
- 一、线性表
- 1、顺序存储
- 2、链式存储
- 特殊链表结构
- 3、顺序存储与链式存储优缺点
- 三、栈
- 1、栈的顺序存储
- 2、栈的进栈出栈操作
- 3、两栈共享空间
- 四、队列
- 1、顺序存储的不足
- 2、循环队列
- 3、队列的链式存储
- 五、作业
一、线性表
定义:零个或多个数据元素的有限序列
要求:第一个元素无前驱,最后一个元素无后继,其他元素都有且只有一个前驱和后继。
思考:循环链表?双向链表?
线性表的抽象数据类型ADT(书p45),其代码表示:
在list.h头文件中
#include 1、顺序存储
定义:用一段连续的地址存储单元依次存储线性表的数据元素。
要求:数据元素类型相同。
所以我们可以用一维数组来实现顺序存储结构。

第i个数据元素ai的存储位置:LOC(ai) = LOC(a1)+(i - 1)* c (c为每个数据元素占据的存储单元)
#define MAXSIZE 100 /*初始化空间分类量(内存分配)*/
//增强代码可读性
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
typedef int ElemType;
typedef int Status;
/**
* 线性表的声明
*/
typedef struct list {
//数据元素
ElemType data[MAXSIZE];
//线性表的长度
int length;
}SqList;
由于查找,修改操作过于简单,我们主要讲插入删除操作
首先分清这三个概念
下标:从0开始,例如a0,a1
第i个:从1开始,例如第一个元素(a0),第n个元素(an-1)
线性表长度L->length:数据元素的个数 n
/**
* 插入条件:线性表L已经存在,且1 <= i <= listLength(L)
* 操作:在线性表L中第i个位置之前插入元素e
* @param L 线性表L
* @param i 位置坐标
* @param e 插入元素
* @return 状态值
*/
Status listInsert(SqList* L,int i,ElemType e) {
//1.算法的健壮性
if (L->length == MAXSIZE) {/*线性表已经满了*/
return ERROR;
}
/*或者if (listLength(*L) == MAXSIZE) {
return ERROR;
}*/
if (i < 1 || i > L->length + 1) {/*i不在插入的范围内*/
return ERROR;
}
if (i <= L->length) { /*此时i满足条件,并且不是在表尾进行插入*/
//将第i个位置后面的元素,依次后移才有位置进行插入
for (int k = L->length - 1; k >= i - 1; k++) {
L->data[k + 1] = L->data[k];
}
}
L->data[i - 1] = e; /*将新元素插入*/
L->length++; /*长度加1*/
return OK;
}
/**
* 删除条件:线性表L已经存在,且1 <= i <= listLength(L)
* 在线性表L删除第i个位置的元素,并将其值返回给e
* @param L 线性表L
* @param i 位置坐标
* @param e 删除位置的元素值
* @return 状态值
*/
Status listDelete(SqList* L,int i,ElemType* e) {
//1.算法的健壮性
if (L->length == 0) {/*线性表已经空了*/
return ERROR;
}
/**或者 if (isEmpty(*L)) {
return ERROR;
}*/
if (i < 1 || i > L->length) {/*i不在删除的范围内*/
return ERROR;
}
*e = L->data[i - 1]; /*取删除位置的值赋给e*/
if(i < L->length) { /*如果删除位置不是在表尾*/
//将删除位置后的后继元素前移
for (int k = 0; k < L->length; ++k) {
L->data[k - 1] = L->data[k];
}
}
L->length--; /*长度减1*/
return OK;
}
2、链式存储
单链表的创建
/**
* 创建一个单链表
* @param L 单链表头指针
* @param n 单链表元素个数
*/
void createList(LinkList* L,int n) {
//定义两个指针,分别是用于申请内存的临时指针,一个是最后用于指向尾结点的指针
LinkList* p, r;
L = (LinkList*)malloc(sizeof(Node));
r = L;
for (int i = 0; i < n; i++) {
p = (LinkList*)malloc(sizeof(Node));
r->next = p;
r = p; /*循环创建动起来*/
}
r->next = NULL;
}
CRUD操作参照单链表讲义链表讲义,这里不再赘述。
头指针与头结点区别
头结点:(可有可无)放在第一个结点前,一般存放链表长度等,有了头结点对于删除第一个元素就跟其他元素操作统一了。
头指针:指向第一个结点,如果有头结点就指向头结点。
特殊链表结构
(1)静态链表(了解即可):用数组描述的链表,简单说就是结构体数组,结构体有个游标(cur)指向下一个结构体的下标。
(2)循环链表
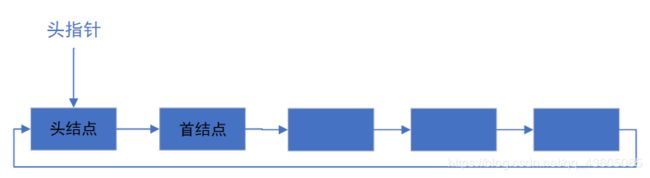
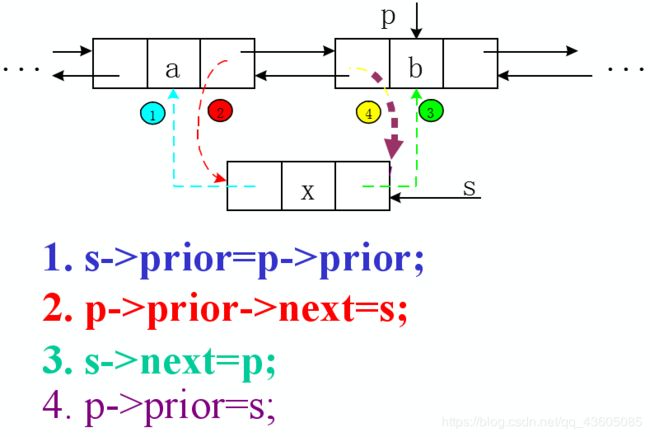
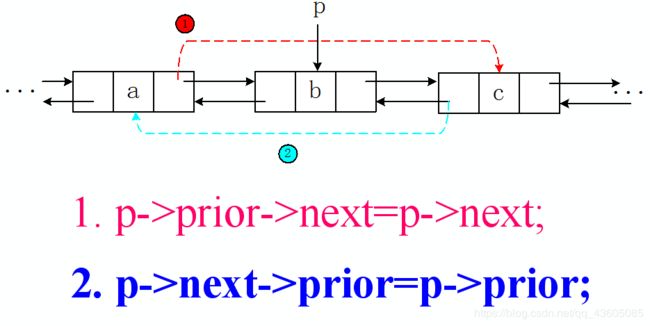
(3)双向链表
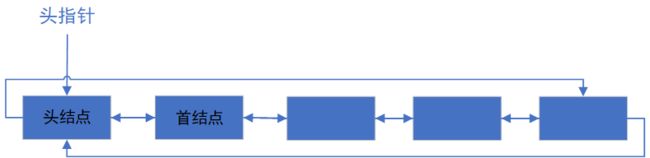
注意:不要忘记头结点的前驱指向最后一个结点。
/**
* 双向链表的声明
*/
typedef struct dulNode {
//数据元素
ElemType data;
struct dulNode* prior; /*直接前驱结点*/
struct dulNode* next; /*直接后继结点*/
}dulNode;
插入、删除操作特别注意代码的书写顺序
3、顺序存储与链式存储优缺点
对于我们如何选择顺序存储或者是链式存储,我们先来比较他们的优缺点
(1)插入:要在线性表中插入元素,显然顺序存储时间复杂度O(n),而链式存储时间复杂度O(1)
(2)删除:要在线性表中删除元素,显然顺序存储时间复杂度O(n),而链式存储时间复杂度O(1)
(3)查找:要在线性表中查找元素,显然顺序存储时间复杂度O(1),而链式存储时间复杂度O(n)
(4)修改:要在线性表中修改元素,显然顺序存储时间复杂度O(1),而链式存储时间复杂度O(n)
结论:
(1)线性表需要频繁的查找,建议顺序存储。如果需要频繁的插入删除,则选择链式存储为宜(例如学生管理系统)。
(2)元素个数较大或者根本不知道有多少个,用链式存储为宜。但是如果事先知道大致长度,且长度不是特别大(例如:一年12个月)顺序存储效率高,不需要频繁申请内存。
三、栈
定义:限定仅在表尾进行操作的线性表。(就是个只能在一端操作,且有栈顶指针的数组)
允许操作的一端叫做栈顶(top),另一端叫做栈底(base),栈是遵循先进后出原则设计的线性表。
例如:网页的返回键,数制转换,递归函数。
栈的抽象数据类型ADT(书p91),其代码表示:
//在stack.h头文件中
#include 1、栈的顺序存储
/**
* 栈的声明
*/
typedef struct Stack {
//数据元素
SElemType data[MAXSIZE];
//栈顶位置
int top;
}SqStack;
注意:
(1)定义一个top变量来指示栈顶元素在数组中的位置。
(2)当栈存在一个元素的时候,top等于0(即数组中的a0,下标为0),所以我们初始化栈时,必须将空栈top=-1,这是空栈的判定条件。
而栈的链式存储做的问题,我们一般用含尾指针的单链表就可以解决,所以链栈显得不重要,则不再赘述。
2、栈的进栈出栈操作
/**
* 若栈存在,插入新元素e到S中作为栈顶元素
* @param S 栈S
* @param e 插入元素
* @return 状态值
*/
Status push(SqStack* S,SElemType e) {
//栈满了
if (S->top == MAXSIZE - 1) {
return ERROR;
}
S->top++;
S->data[S->top] = e;
return OK;
}
/**
* 删除S中的栈顶元素,用e来接收
* @param S 栈S
* @param e 接收的栈顶元素
* @return 状态值
*/
Status pop(SqStack* S, SElemType* e) {
//栈为空
if (S->top == -1) {
return ERROR;
}
*e = S->data[S->top];
S->top--;
return OK;
}
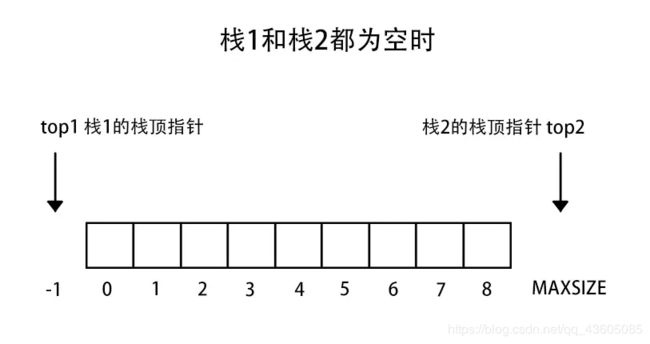
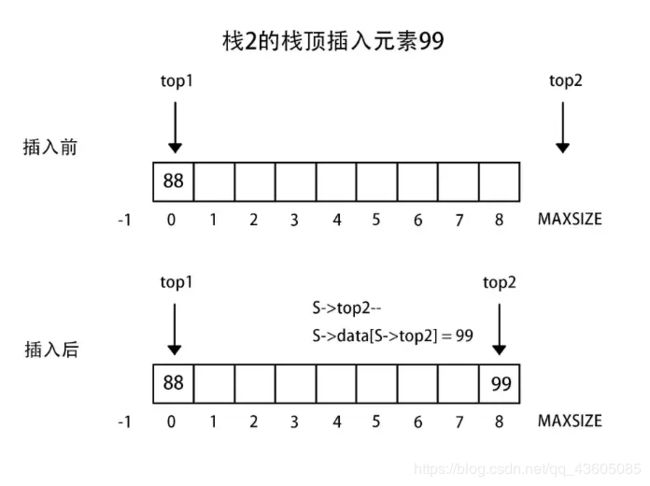
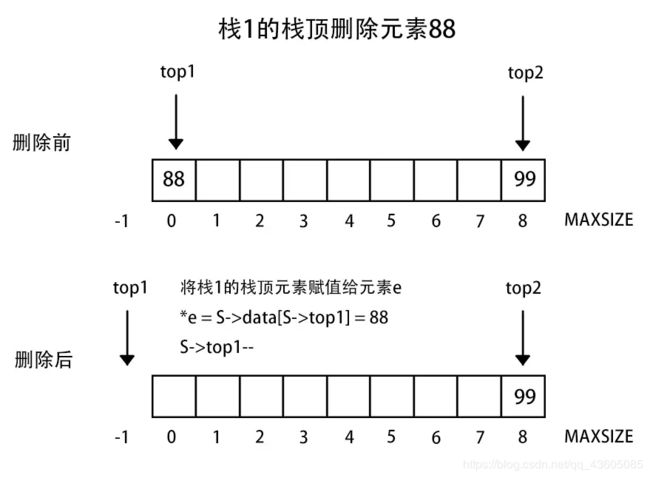
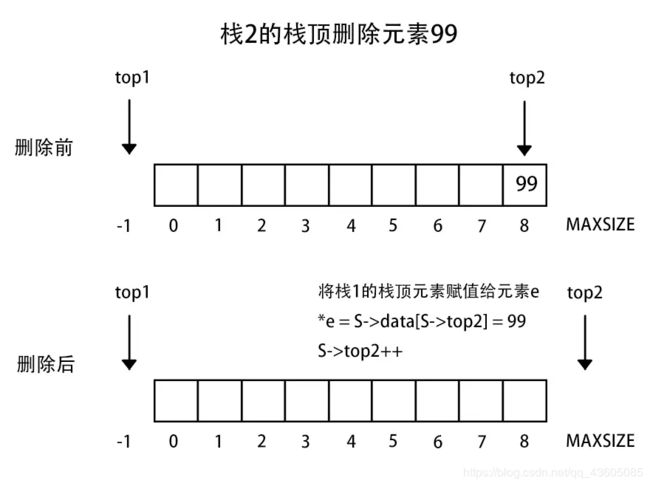
3、两栈共享空间
两个相同的栈,我们可以使用一个数组进行存储两个栈,只不过他们在一块数组里。这样一个栈增加另一个栈缩短的数据结构一般例如买卖股票,你买入,就会有人卖出。
做法:数组有两个端口(0和MAXSIZE - 1),两个栈如果增加元素,就是两个端口向中间延伸。top1和top2分别指向-1和MAXSIZE。
/**
* 两栈共享空间
*/
typedef struct SqDoubleStack {
SElemType data[MAXSIZE];
//栈1和栈2的栈顶位置
int top1;
int top2;
}SqDoubleStack;
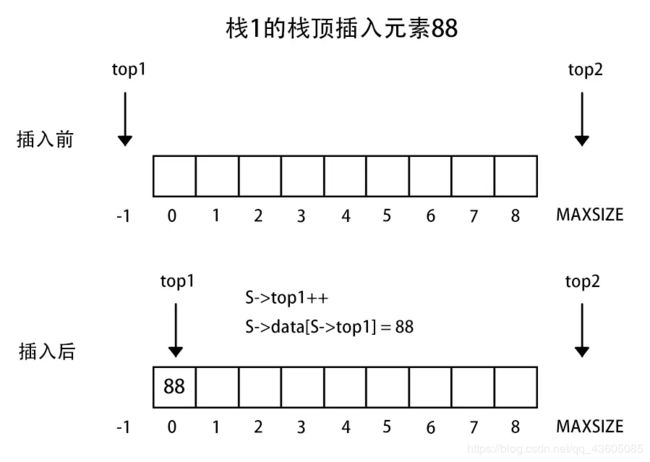
注意:栈1空和栈2空的条件简单,即top1 = -1或者top = MAXSIZE。但是栈满的条件(即两个指针向中间靠拢)即top1 + 1 == top2
/**
* 若栈存在,插入新元素e到S中作为栈顶元素
* @param S 栈S
* @param e 插入元素
* @param stacknumber 哪个栈入栈
* @return 状态值
*/
Status push(SqDoubleStack* S,SElemType e, int stacknumber) {
//栈满了
if (S->top1 + 1 == S->top2) {
return ERROR;
}
//分情况进栈
if (stacknumber == 1) {
S->top1++;
S->data[S->top1] = e;
}
else if (stacknumber == 2) {
S->top2--;
S->data[S->top2] = e;
}
return OK;
}
/**
* 删除S中的栈顶元素,用e来接收
* @param S 栈S
* @param e 接收的栈顶元素
* @param stacknumber 哪个栈出栈
* @return 状态值
*/
Status pop(SqDoubleStack* S, SElemType* e, int stacknumber) {
//因为两栈空,判断条件不同
if (stacknumber == 1) {
//栈1空
if (S->top1 == -1) {
return ERROR;
}
*e = S->data[S->top1];
S->top1--;
}
else if (stacknumber == 2) {
//栈2空
if (S->top2 == MAXSIZE) {
return ERROR;
}
*e = S->data[S->top2];
S->top2++;
}
return OK;
}
四、队列
定义:是只允许在一端插入,另一端进行删除的线性表。太常见了,就不举例了。
队列的抽象数据类型ADT(书p112),其代码表示:
//在queue.h头文件中
#include 1、顺序存储的不足
队列的顺序存储与数组类似,只不过在队尾加上rear(末尾下标),声明就不再赘述。
不足:队列元素的出列是在队头,下标为front的位置(即队头不是一直是0)。队列元素的入队在队尾,下标为rear位置。rear一直入队,front一直出队,可能当rear都到了MAXSIZE之外了(数组越界),但是front前面还有很多空缺,就要就出现了 “假溢出”。
2、循环队列
解决上述假溢出的办法就是后面满了,就在前面补上,头尾相接的循环队列。
循环队列的顺序存储结构
/**
* 循环队列声明
*/
typedef struct queueInfo {
//数据元素
QElemType data[MAXSIZE];
//头尾指针
int front;
int rear; /*rear指向队尾的下一个位置(即将插入的位置)*/
}QueueInfo;
注意:在求循环队列长度和入队出队操作**需要注意。
(1)循环队列长度: length = (Q.rear - Q.front + MAXSIZE) % MAXSIZE
(2)循环队列的队列满条件:((Q->rear + 1) % MAXSIZE == Q->front)
(3)循环队列的队列空条件:(Q->front == Q->rear)
代码如下:
/**
* 返回队列Q的元素个数
* @param Q 循环队列
* @return 元素个数
*/
int queueLength(SqQueue Q) {
return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}
/**
* 若队列存在且未满,插入新元素e到队列的队尾
* @param Q 循环队列
* @param e 插入元素
* @return 状态值
*/
Status enQueue(SqQueue* Q, QElemType e) {
//如果队列满了
if ((Q->rear + 1) % MAXSIZE) {
return ERROR;
}
//rear指向后一位(即将插入的位置)
Q->data[Q->rear] = e;
Q->rear = (Q->rear + 1) % MAXSIZE;//如果假溢出,就到数组前面去
return OK;
}
/**
* 删除队列的队头元素,用e返回其值
* @param Q 循环队列
* @param e 删除的元素值
* @return 状态值
*/
Status deQueue(SqQueue* Q, QElemType* e) {
//如果队列空了
if (Q->front == Q->rear) {
return ERROR;
}
*e = Q->data[Q->front];
Q->front = (Q->front + 1) % MAXSIZE; //同理
return OK;
}
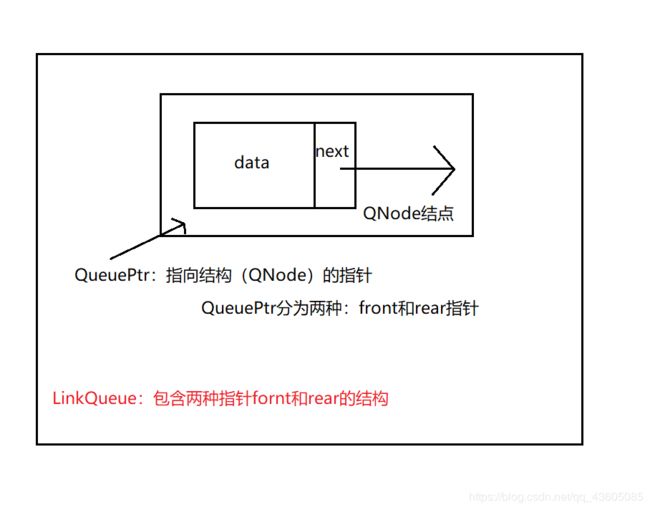
3、队列的链式存储
而队列的链式存储其实就是head指针位置取元素和rear指针位置加元素的单链表,这里则不再赘述。
需要注意的是:
链队列的结构代码中
typedef struct QNode {
QElemType data;
struct QNode* next;
}QNode,*QueuePtr;
//QueuePtr为指向结点的指针
//这个结构里面包含两种QueuePtr(队头、队尾指针)
typedef struct queuePtr {
QueuePtr front, rear;
}LinkQueue;
例如:LinkQueue Q中
Q->rear->data表示为:Q这个链队列所指向的尾指针所指向的节点数据
Q->front->next同理为:Q这个链队列所指向的头指针所指向的节点的后继节点*
五、作业
1、在数据结构中,从逻辑上可以把数据结构分为( )
A. 动态结构和静态结构
B. 紧凑结构和非紧凑结构
C. 线性结构和非线性结构
D. 内部结构和外部结构
2、在存储数据时,通常不仅要存储各数据元素的值,而且还要存储( )
A. 数据的处理方法
B. 元素的类型
C. 数据元素之间的关系
D. 数据存储的方法
3、与单链表相比,双链表的优点之一是( )
A. 插入、删除操作更简单
B. 可以进行随机访问
C. 可以省略表头指针或表尾指针
D. 顺序访问相邻节点更灵活
4、如果对线性表的操作只有两种,即删除第一个元素、在最后一个元素当当后面插入新元素,则最好使用( )
A. 只有表头指针没有表尾指针的循环单链表
B. 只有表尾指针没有表头指针的循环单链表
C. 非循环双链表
D. 循环双链表
5、一个栈的进栈顺序是a、b、c、d、e,则栈不可能出现的输出顺序是( )
A. edcba
B. decba
C. dceab
D. abcde
6、若已知一个进栈序列是1、2、3、···· · · 、n,则其输出序列为p1、p2、p3、· · · 、pi、· · · 、pn,若p1 = n,则pi为( )
A. i
B. n-i
C. n-i+1
D. 不确定
7、输入序列为ABC,可变为CBA时,经过的栈操作为( )
A. push, pop, push, pop, push, pop
B. push, push, push, pop, pop, pop
C. push, push, pop, pop, push, pop,
D. push, pop, push, push, pop, pop
8、若采用顺序栈存储方式存储,现两栈共享空间V[1 m],top[1], top[2]分别代表第1个和第2个栈的栈顶,栈1的底在V[1], 栈2的底在V[m],则栈满的条件是( )
A.|top[2] – top[1]| = 0
B.top[1] + 1 = top[2]
C.top[1] + top[2] = m
D.top[1] = top[2]
9、数组A中,每个元素的长度为3个字节,行下标i从1到8,列下标从1到10,从首地址SA开始连续存放的存储器内,该数组按行进行存放,元素A[8][5]的起始地址为( )
A. SA+141
B. SA+144
C. SA+222
D. SA+255
10、循环队列用数组存放其元素值A[0,m-1], 已知其头尾指针分别是rear和front,则当前队列的元素个数是( )
A. rear-front+1
B. rear-front-1
C. rear-front
D. (rear-front+m)%m
11、判断一个循环队列QU(最多元素为m0)为满的条件是( )
A. QU.front == QU.rear
B. QU.front != QU.rear
C. QU.front == (QU.rear + 1)%m0
D. QU.front == QU.rear – 1
12、利用栈实现十进制到二进制的转换(利用除2取余法)
输入:45
输出:10 1101
13、循环队列的应用——舞伴配对问题:在舞会上,男、女各自排成一队。舞会开始时,依次从男队和女队的队头各出一人配成舞伴。如果两队初始人数不等,则较长的那一队中未配对者等待下一轮舞曲。假设初始男、女人数及性别已经固定,舞会的轮数从键盘输入。试模拟解决上述舞伴配对问题。要求:从屏幕输出每一轮舞伴配对名单,如果在该轮有未配对的,能够从屏幕显示下一轮第一个出场的未配对者的姓名。(分别依次输入男姓名、女姓名,并输出每轮配对结果,以下为一次标准输入输出,两队人数由主函数固定)
输入第1个男人名:a
输入第2个男人名:b
输入第3个男人名:c
输入第4个男人名:d
输出男人队列:a b c d
输入第1个女人名:A
输入第2个女人名:B
输入第3个女人名:C
输入第4个女人名:D
输入第5个女人名:E
输入第6个女人名:F
输出女人队列:A B C D E F
配对者:a–A
配对者:b–B
配对者:c–C
配对者:d–D
未配对的第一个出来的是:E
配对者:a–E
配对者:b–F
配对者:c–A
配对者:d–B
未配对的第一个出来的是:C
配对者:a–C
配对者:b–D
配对者:c–E
配对者:d–F
未配对的第一个出来的是:A