下面这句话是真的,
上面那句话是假的。
这就是一个典型的因自指而产生的悖论,也叫说谎者悖论。与之等价的还有一种表达:
“我说的这句话是假的。”
更为著名的自指悖论是理发师悖论,罗素在1901年为了比较形象地讲解罗素悖论而给出的一个比喻:
小镇的理发师说:我只给,且一定要给这个镇子里不给自己理发的人理发。
罗素给出了这种悖论的数学表达方法,A={x|x ∉ x},那么此时,如果A∈A,那么我们会推导出A∉A;反之如果说A∉A,那么我们会推导出A∈A。任何一个单方面的判断都会导致一个与之相悖的结论出现。
这种悖论在现实世界中最为明显的表达,就是停机问题。因为当计算机遇到这种悖论时,它可不会像人一样自己笑一笑就跳过去,而只会不停地进行死循环——我们马上就会讲到,计算机连判断是否会死循环都做不到——然后,死机,蓝屏:
这一篇作为读书笔记,我进入了一个自己完全不了解的领域。很多证明我看不懂——在很艰难的尝试之后,确实没懂——于是我能做的只是将自己得到的印象写下来。
对数学本身的研究叫做“元数学”。另一方面,因为数学与逻辑学的联系是如此紧密,以至于经常有数学家认为数学只是逻辑学的一部分——或者有时候反过来,逻辑学只是数学的一部分。所以元数学经常也被叫做元逻辑。
数学的发展基于严格的理性推理,但在此之前,元数学就需要告诉大家,数学推理的本质是什么,什么样的推理是合法的而什么样的推理不合法。为了排除自然语言对数学的影响,元数学就建立了一套数学自己的符号系统。这种将推理方法完全规范化的工作就是所谓的“形式化”。所有的数学都要在这个形式化的系统之内进行工作,于是我们可以将推理的思维过程进行机械化。而悖论就是在这些数学尝试的进展过程中发挥其破坏力的。
我们在上面看到,罗素悖论产生于“集合”这个最为基本的概念之上。也就是说,以如此定义的概念进行推理,其必然会产生悖论。除此之外,我们也很有理由去怀疑,既然连集合论这种具体理论都能如此轻易地产生悖论,那我们的数学大厦,真的是建立在一个坚固的基础之上吗?如果这种悖论必然会出现,那么,几乎所有的数学都很可疑。
在这种背景之下,罗素为消除这种悖论进行了一系列努力。
我们上面说到过这种悖论的根源在于“自指”,即是说,当一个集合涉及到其自身时,其必然会产生悖论。比较明显易懂的例子像是:
“我现在在思考。”
“这句话是本文最后一句话。”
等等。
罗素在《数学原理》里进行了一种尝试,他对“集合”这个概念本身进行了变动,使其含义中多了一个“阶”。有一个“阶”最低的集合,这种集合只能包含有元素而不包含有任何集合。高阶的集合可以包含有低阶集合,反之则不行。这样一来,罗素通过定义的方式强行将“自指”从数学中驱除了出去——不存在任何可以包含有自身的集合。
从那个说谎者悖论上讲,第一个句子“下面这句话是假的”,它如果要谈论下一个句子,那证明其“阶”要更高;但第二个句子“上面这句话是真的”,这句话需要比上一句的“阶”高才行。根据罗素的定义,这种句子不可能存在于严格语言层次上,所以在系统中并不可能出现,是无意义的。于是他将这个悖论放逐了。
幸好罗素只是在数学中进行了这个工作,否则,如果他将所有的语言都进行这样的改造以去除悖论,那我们永远不要想在任何地方提到自己。像“我”、“本文”、“这句话”等等等等的语言都是绝对禁止的——这是自指,会产生悖论。
虽说罗素的这一工作看起来很生硬,但总之他确实保证了数学的一致性。但另一方面,仍然没有任何人敢于保证通过使用罗素给出的方法就一定不会产生矛盾。
于是希尔伯特就提出了这么一个挑战:严格地论证《数学原理》一书中定义的系统既是一致的又是完全的。即是说,他想证明,《数学原理》一书里的系统是绝对不会自相矛盾产生悖论的,又可以从中推导出所有的数学。当然,这看起来有点循环论证:你要怎么用你给出的推理方法推理出你的推理方法是完全正确的?
但哥德尔在1931年发表了一篇引文,提出了哥德尔不完备定理,几乎彻底粉碎了这种形式化的努力。
事实上哥德尔这个人在1929年的时候发现了一个叫“哥德尔完备定理”的东西,这个定理一压被认为是希尔伯特方案的最大成果之一。他证明了所有在一阶谓词演算中的所有推理都是“可证明的”,换句话说,至少在一阶谓词上,这个系统本身就可以证明其系统是完备的。但他在1931年新抛出来的这篇论文完全粉碎了同时代数学家们在这个结论之上的所有努力。
哥德尔不完备定理表明:
数论的所有一致的公理化形式系统都包含有不可判定的命题。
也就是说,在一个形式化系统内,其中永远有一些命题我们没办法去证明或证伪。除此之外,我们甚至没办法知道这些命题都是什么。
这也是到现在我们的电脑仍然会死机蓝屏的最根本原因。即便进行了形式化之后,电脑仍然没办法对一个程序是否会进入死循环进行判断——如果说我们想加入一个检测程序,即是说如果发现进入了死循环即强行终止,这个检测程序本身也会陷入了停机问题。图灵在1936年给出过证明,不存在通用算法可以解决图灵机的停机问题。换言之,这个问题不可判定。
哥德尔不完备性定理几乎直接触及到了人类理性的极限,他证明形式化的机械式推理永远存在其自身无法证明的命题,而我们还不知道这些是哪些命题。所谓的人类理性,其所能触及到的范围就只有这么多了。对于人工智能的悲观态度多数来源于此,因为我们人类的理性极限是悖论,我们人类思考时可以跨越过悖论,但机械不行,机械只会死机。
说到这里我似乎突然真正了解了在《禅与摩托车维修艺术》里斐德洛提到的“良质”。
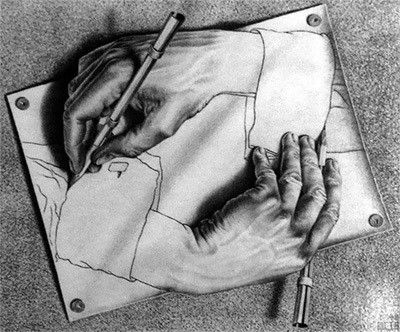
关于巴赫、艾舍尔,他们的音乐与艺术我虽然也觉得很美很震撼,但总体而言,我并不太认同作者提到的这是悖论与不完备在不同领域的表达。艾舍尔画作中大量的数学表达与悖论相当有吸引力,像《画手》这种:
作者提到巴赫的数首无限循环的卡农,像那首《Canon per tonos》。但总体而言,我觉得其尝试与数学的哥德尔还是有相当差别的。