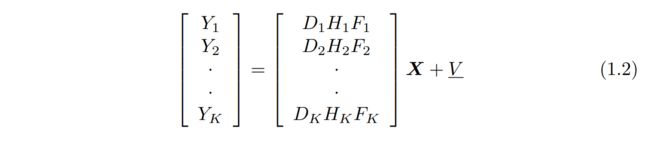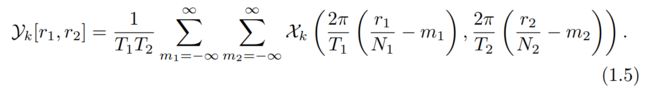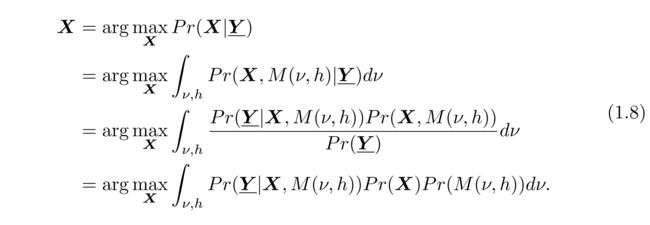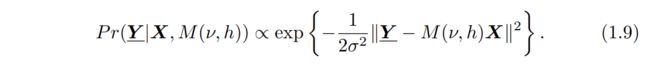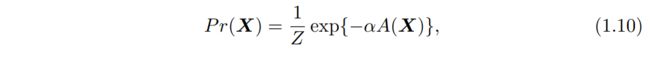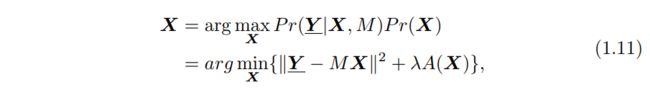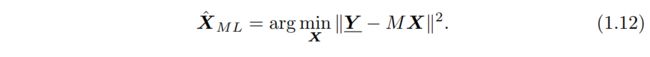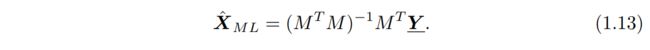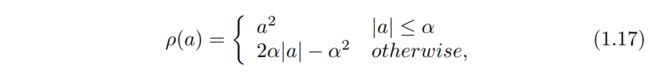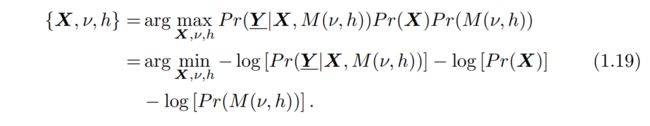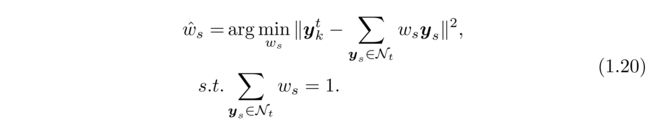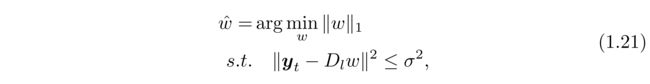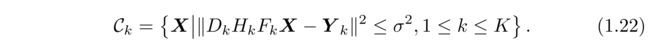Limityoung
Limityoung

影像超分辨率：历史回顾和未来的挑战

原文标题：Image super-resolution: Historical overview and future challenges
原文网址：http://www.ifp.illinois.edu/~jyang29/papers/chap1.pdf
作者：Jianchao Yang (University of Illinois at Urbana-Champaign)
Thomas Huang (University of Illinois at Urbana-Champaign)

1.1 超分辨率的简介

在大多数数字成像应用中，通常需要高分辨率图像或视频用于以后的图像处理和分析。对高图像分辨率的渴望源于两个主要的应用领域：改进图像信息用于人类解释; 并帮助表示用于自动机器感知。图像分辨率描述图像中包含的细节，分辨率越高，图像细节越多。 数字图像的分辨率可以以许多不同的方式分类：像素分辨率，空间分辨率，光谱分辨率，时间分辨率和辐射分辨率。在本文中，我们主要对空间分辨率感兴趣。

空间分辨率：数字图像由称为像素的小图像元素组成。 空间分辨率是指图像中的像素密度，以每单位面积的像素值为单位。图1.1显示了确定成像系统空间分辨率的经典测试目标。

影像超分辨率：历史回顾和未来的挑战_第1张图片
图1.1 1951年美国空军的分辨率测试目标，一种用于确定成像传感器和成像系统空间分辨率的经典测试目标。

图像空间分辨率首先受成像传感器或成像采集装置的限制。现代图像传感器通常是电荷耦合器件（CCD）或互补金属氧化物半导体（CMOS）有源像素传感器。这些传感器通常以二维阵列排列以捕获二维图像信号。传感器尺寸或等效的每单位面积的传感器元件的数量首要地决定了要捕获的图像的空间分辨率。传感器密度越高，成像系统的空间分辨率越高。由于低空间采样频率的混叠，具有不充足探测器的成像系统将产生具有块效应的低分辨率图像。为了增加成像系统的空间分辨率，一种直接的方法是通过减小传感器尺寸来增加传感器密度。然而，随着传感器尺寸减小，入射在每个传感器上的光量也减少，从而引起所谓的散粒噪声。而且，传感器的硬件成本随着传感器密度或相应的图像像素密度的增加而增加。因此，对传感器尺寸的硬件限制限制了可以捕获的图像的空间分辨率。

虽然图像传感器限制了图像的空间分辨率，但由于镜头模糊（与传感器点扩散函数（PSF）相关联），镜头像差效应，光圈衍射和运动导致的光学模糊，图像细节（高频带）也受到光学器件的限制。构造成像芯片和光学组件以捕获非常高分辨率的图像非常昂贵并且在大多数实际应用中不实用，例如广泛使用的监视相机和手机内置相机。除了成本之外，监控摄像机的分辨率也受到摄像机速度和硬件存储的限制。在诸如卫星图像的一些其他场景中，由于物理限制，难以使用高分辨率传感器。解决该问题的另一种方法是接受图像劣化并使用信号处理来对捕获的图像进行后处理，以便将计算成本与硬件成本进行权衡。这些技术具体称为超分辨率（SR）重建。

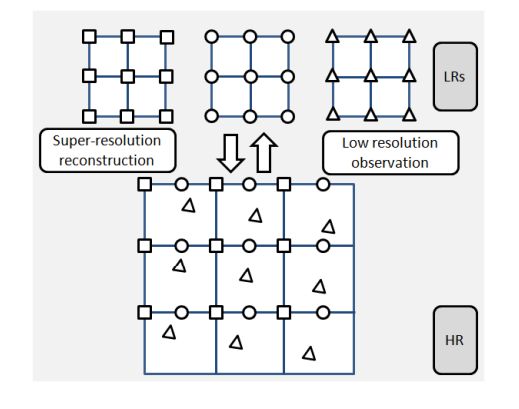
超分辨率（SR）是从若干观察到的低分辨率（LR）图像构建高分辨率（HR）图像的技术，从而增加高频分量并消除由低分辨率相机的成像过程引起的劣化。SR背后的基本思想是组合多个低分辨率帧中包含的非冗余信息以生成高分辨率图像。与SR密切相关的技术是单图像插值方法，其也可用于增加图像尺寸。然而，由于没有提供附加信息，单个图像插值的质量由于问题的不适定性而受到很大限制，并且丢失的频率分量无法恢复。但是，在SR设置中，可以使用多个低分辨率观测值进行重建，从而使问题得到更好的约束。包含在这些LR图像中的非冗余信息通常通过它们之间的子像素移位来引入。这些子像素移位可能由于成像系统和场景之间的不受控制的运动（例如，物体的运动）或由于受控的运动而发生，例如，卫星成像系统以预定的速度和路径绕地球运行。

每个低分辨率帧都是对真实场景的削弱的，别名的观察。只有在这些低分辨率帧1之间存在子像素运动时SR才是可能实现的，这样可以更好地调节不适定的上采样问题。图1.2显示了描述SR重建基本思想的简化图。

注释1：主流的SR技术依赖于运动，尽管有些工作使用散焦作为提示。

影像超分辨率：历史回顾和未来的挑战_第2张图片
图1.2 从多个低分辨率帧进行超分辨率重建的基本思想。子像素运动提供低分辨率帧之间的互补信息，使得SR重建成为可能。

在成像过程中，摄像机捕获若干LR帧，这些LR帧从HR场景下采样，子像素在彼此之间移位。 SR构造通过将LR观察对齐至子像素精度并将它们组合成HR图像网格（插值）来反转该过程，从而克服了相机的成像限制。SR（其中一些在本书中描述）出现在许多领域，例如：

1.监控视频[20,55]：用于人类感知的视频中的帧冻结和缩放感兴趣区域（ROI）（例如，查看视频中的车牌），自动目标识别的分辨率增强（例如，尝试识别犯罪分子的面部）。

2.遥感[29]：提供相同区域的若干图像，并且可以寻找改进的分辨率图像。

3.医学成像（CT，MRI，超声等）[59,70,47,60]：可以获得分辨率质量有限的几个图像，并且可以应用SR技术来增强分辨率。

4.视频标准转换，例如 从NTSC视频信号到HDTV信号。

本章的目的是介绍SR研究领域，解释SR的一些基本技术，文献概述，以及未来研究中一些具有挑战性的问题的讨论。

1.2 符号

在讨论SR技术之前，我们将介绍我们在本章中使用的符号。大写粗体字母X和Y分别表示HR和LR图像的字典顺序的矢量形式。小写粗体字母x和y分别表示HR和LR图像块(image patches)的字典顺序的矢量形式。带下划线的大写粗体字母用于表示多个向量的向量级联，例如：Y_是Yk (k = 1, 2, ..., K)的向量级联。我们使用普通大写符号来表示矩阵，使用普通小写符号来表示标量。

1.3 用于超分辨率的技术

自从Tsai和Huang [99]于1984年的开创性工作以来，SR重建一直是最活跃的研究领域之一。在过去二十年中已经提出了许多技术[4,65]，代表了从频域到空间域的方法，以及从信号处理角度到机器学习角度。早期关于超分辨率的研究主要遵循[99]的理论，通过探索傅里叶变换的移位和混叠特性。然而，这些频域方法在它们可以处理的图像观察模型中受到很大限制，并且实际问题要复杂得多。目前，研究人员通常主要在空间领域解决这个问题，因为它可以灵活地模拟各种图像质量下降。本节从图像观察模型开始讨论这些技术。

1.3.1 图像观察模型

由于硬件限制，获取具有各种劣化的图像，数字成像系统并不完美。例如，有限光圈大小导致光学模糊，由点扩散函数（PSF）建模。有限光圈时间导致运动模糊，这在视频中非常常见。有限的传感器尺寸导致传感器模糊; 通过在传感器区域上的积分而不是脉冲采样来生成图像像素。有限的传感器密度导致混叠效应，限制了所获得图像的空间分辨率。这些降级在不同的SR技术中完全或部分建模。

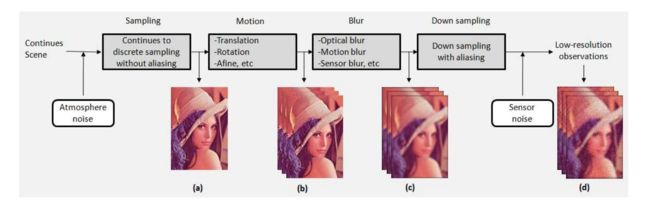
影像超分辨率：历史回顾和未来的挑战_第3张图片
图1.3 将高分辨率图像与低分辨率观察帧相关联的真实成像系统的观察模型，其中场景和相机之间存在运动。

图1.3显示了将HR图像与LR视频帧相关联的典型观察模型，如文献[65,82]中所介绍的。成像系统的输入是连续的自然场景，很好地近似为带限信号。在到达成像系统之前，这些信号可能被大气湍流污染。对奈奎斯特速率以上的连续信号进行采样会产生我们想要的高分辨率数字图像（a）。在我们的SR设置中，通常在相机和场景之间存在某种运动以进行捕捉。摄像机的输入是场景的多个帧，通过可能的局部或全局移位连接，得到图像（b）。通过相机，这些与运动相关的高分辨率帧将产生不同类型的模糊效果，例如光学模糊和运动模糊。然后，通过落入每个传感器区域的图像的积分，在图像传感器（例如CCD检测器）处将这些模糊图像（c）下采样为像素。这些下采样图像还受到传感器噪声和滤色噪声的影响。最后，由低分辨率成像系统捕获的帧是模糊，降低的和带有噪声版本的基础真实场景。

令X表示期望的HR图像，即，从带限连续场景的奈奎斯特采样率以上采样的数字图像，并且Yk是来自相机的第k次LR观察。X和Y'ks以字典顺序表示。假设摄像机捕获X的K个LR帧，其中LR观察与HR场景X的关系是：

其中Fk编码第k帧的运动信息，Hk模拟模糊效果，Dk是下采样算子，Vk是噪声项。这些线性方程可以重新排列成一个大的线性系统：

影像超分辨率：历史回顾和未来的挑战_第4张图片

或是等价地：

涉及的矩阵Dk，Hk，Fk或M非常稀疏，这种线性系统通常是不适定(ill-posed)的。此外，在实际成像系统中，这些矩阵是未知的，需要从可用的LR观察进行估计，使问题更加恶劣。因此，对于高分辨率图像的适当的先验正则化始终是期望的并且通常甚至是至关重要的。接下来，我们将介绍文献中提出的一些基本的超分辨率技术，并概述最近的发展。

1.3.2 频域下的超分辨率

超分辨率的开创性工作追溯到Tsai和Huang [99]，其文章中作者通过基于连续和离散傅里叶变换的移位和混叠特性的频域公式将高分辨率图像与多个移位的低分辨率图像相关联。设 x(t1, t2) 表示连续的高分辨率场景。全局平移产生K个移位图像， x(t1, t2) = x(t1+△k1, t2+△k2) ，其中k = 1,2, ..., K，△k1和△k2是任意但已知的移位。场景的连续傅里叶变换（CFT）由χ(u1, u2)给出，而被翻译的场景由χk(u1, u2)给出。然后通过CFT的移位特性，可以将移位图像的CFT写为：

使用采样周期T1和T2对移位的图像进行脉冲采样，以产生观察到的低分辨率图像yk [n1, n2] = xk (n1T1 + △k1, n2T2 + △k2)，其中n1 = 0,1,2, ..., N1-1 和 n2 = 0,1,2, ..., N2-1。用Yk [r1, r2]表示这些低分辨率图像的离散傅里叶变换（DFT）。移位图像的CFT通过混叠属性与其DFT相关：

假设χ(u1, u2)是带限的，| χ(u1, u2) | = 0 对于| u1 | ≥ (N1π) / T1, | u2 | ≥ (N2π) / T2，结合方程1.4和方程1.5我们将Yk [r1, r2]的DFT系数与矩阵形式的x(t1, t2)的未知CFT样本相关联2：

注释2：严格地说，下标{r1, r2}应该用在下面的等式中。我们为了整洁的演示文稿省略了那些。

其中Y_是K×1列向量，其中第k个元素是DFT系数Yk [r1, r2]，X_是包含未知CFT系数x(t1, t2)的N1N2×1列向量，Φ是一个将Y_和X_关联在一起的K×N1N2矩阵。公式1.6定义了一组线性方程，我们打算从中求解X_，然后使用逆DFT来获得重建图像。

上述用于SR重建的公式假定了一个无噪声以及参数已知的全局平移模型。假设下采样过程是脉冲采样，没有建模传感器模糊效果。沿着这一系列工作，已经提出了许多扩展来处理更复杂的观察模型。Kim等人[49]通过考虑观察噪声和空间模糊来扩展[99]。他们后来在[5]中的工作通过引入Tikohonov正则化[95]进一步扩展了工作。在[89]中，通过将图像划分为重叠块并且分别估计每个局部块的运动来考虑局部运动模型。在[98]中，使用EM算法（最大期望算法）同时完成恢复和运动估计。然而，这些工作的频域SR理论并没有超出最初提出的范围。这些方法在计算上是有效的，但是它们处理更复杂的图像劣化模型的能力受到限制，并且包括各种图像先验作为适当的正则化。后来关于超分辨率重建的工作几乎完全在空间领域。

1.3.3 插值重建：非迭代方法

多年来已经提出了许多空间域方法[4,82,65,2]来克服频域方法的困难。由于HR图像和LR帧在稀疏线性系统1.3中相关，类似于传统的单图像恢复问题[26]，许多灵活的估计器可以应用于SR重建。这些包括最大似然（ML），最大后验（MAP）[84,35]和投影到凸集（POCS）[88]。在本节中，我们从空间域中SR重建的最简单和非迭代正演模型开始，类似于频域方法。

假设Hk是线性空间不变量（LSI）并且对于所有K帧是相同的，我们将其表示为H。假设Fk仅考虑简单的运动模型，例如平移和旋转，那么H和Fk修改了（这里翻译不是很确定 原文使用commute一词）[27,30]，我们得到

这促进了基于插值和恢复的前向非迭代方法。这种方法分为三个阶段：1）低分辨率图像配准; 2）非均匀插值得到Z和 3）去模糊和噪声去除得到X。图1.4显示了这种方法的过程。首先通过一些图像配准算法[77]将低分辨率帧对准至子像素精度。然后将这些对齐的低分辨率帧放在高分辨率图像网格上，其中非均匀插值方法用于填充HR图像网格上的那些缺失像素以获得Z。最后，Z被任何经典去卷积算法去除噪声实现X。Keren等[48]提出了一种基于全局平移和旋转模型的SR重建的早期两步方法。Gross等人 [101]利用Yen [109]和后来的Papulis [64]的广义多通道采样定理，提出了一组空间位移的低分辨率图像的非均匀插值，然后进行去模糊。Nguyen和Milanfar [62]通过利用低分辨率数据中的交错采样结构，提出了一种有效的基于小波的插值SR重建算法。Alam [1]提出了一种基于加权最近邻的有效插值方案，然后使用Wiener滤波来去模糊。着眼于SR重建的特殊情况，其中观测由纯平移、空间不变模糊和加性高斯噪声组成，Elad和HelOr [27]提出了一种计算效率非常高的算法。[52]提出了一种基于三角测量的方法，用于内插不规则采样数据。然而，三角测量方法对于实际应用中通常存在的噪声不稳健。基于归一化卷积[50]，Pham等 [71]为多项式小平面模型提出了鲁棒的确定性和结构自适应适用性函数，并将其应用于不规则采样数据的融合。最近，武田等 [91]提出了一种自适应转向核回归，用于在高分辨率图像网格上进行插值，其中低分辨率图像被记录和映射到这个网格上。

影像超分辨率：历史回顾和未来的挑战_第5张图片
图1.4 基于对齐和去模糊后处理的插值SR方法。

这些插值恢复前向方法直观、简单且计算效率高[30]，[18]，假设观察模型简单。然而，逐步前进的方法不能保证估计的最优性。配准错误很容易传播到后面的处理中。而且，在没有考虑噪声和模糊效果时，插值步骤是次优的。此外，在没有HR图像先验作为适当的正则化，基于插值的方法需要对有限观察进行特殊处理以减少混叠。

1.3.4 统计方法

与插值-恢复方法不同，统计方法将SR重建步骤随机地与最优重建相关联。低分辨率输入中的HR图像和运动可以被视为随机变量。设M(ν, h)表示由运动矢量ν和模糊核h定义的退化矩阵，SR重建可以转换为完整的贝叶斯框架：

影像超分辨率：历史回顾和未来的挑战_第6张图片

注意，X和M(ν, h)在统计上是独立的[35]。这里Pr(Y_|X, M(ν, h))是数据似然，Pr(X)是期望的高分辨率图像上的先验项，Pr(M(ν, h))是运动估计的先验项。公式1.3中的V_通常代表加性噪声，假设为零均值和白高斯随机向量。因此，

Pr(X)通常使用指数形式的吉布斯分布来定义

其中A(X)是非负势函数，Z只是归一化因子。由于对运动估计的积分，方程式1.8中的贝叶斯公式很复杂且难以评估。如果M(ν, h)预先给出或者被估计（表示为M），则等式1.8可以简化为

1.3.4.1 最大似然

如果我们给X假设一个单值先验，则等式1.11简化为最简单的最大似然（ML）估计（假设运动估计为先验）。ML估计器仅依赖于观测值，通过最大化p(Y_|X)寻找最可能的观察的，给出

将方程1.12对X进行微分并将导数设置为零给出了经典的伪逆结果

如果MTM是奇异的，那么问题是不适定的，并且由于M的零空间，存在无限多种可能的解。由于纯粹的代数观点，这自然导致了正则化项，这是唯一的解决方案，尽管可以在MAP框架中解释。对于计算，由于高维度问题，矩阵的直接逆作为MTM在实践中通常是禁止的。例如，如果低分辨率图像的尺寸为100×100并且要被放大到300×300的单个高分辨率帧X，则M的尺寸为90000×90000，需要反转尺寸为90000×90000的矩阵。因此，文献[111]中提出了许多用于解决这一大型稀疏线性方程组的实用方法的迭代方法。

Irani和Peleg提出了一种简单但非常流行的方法，基于计算机辅助断层扫描的误差反投影方案，在[39,40,41]中。该算法通过添加与反投影函数（BPF）卷积的扭曲模拟误差来迭代地更新当前估计：

其中c是常数，hbpf是反投影内核，S↑是上采样算子，Yk^是来自当前HR估计的模拟第k个LR帧。在[41]中，作者通过结合多运动跟踪算法来处理部分遮挡的对象，透明对象和一些感兴趣的对象，将这个想法应用于实际应用。反投影算法在处理具有不同退化过程的许多观察时是简单且灵活的。然而，反投影的解决方案并不是唯一的，这取决于初始化和反投影内核的选择。如[26]和[10]所示，反投影算法正是ML估计器。BPF的选择暗示了关于观察到的低分辨率像素的噪声协方差的一些潜在假设[10]。Tom等人将运动估计M(ν)估计为未知,在[98]提出了一种ML SR图像估计算法，用于同时估计子像素移位、图像噪声和HR图像。所提出的ML估计由期望最大化（EM）算法处理。

如在图像去噪和单图像扩展情况中那样，在SR中观察数量受限的没有正则化的直接ML估计器可能严重不适，特别是当变焦因子很大（例如，大于2）时。ML估计器通常对噪声，配准估计误差和PSF估计误差非常敏感[10]，因此总是需要对可行解空间进行适当的正则化。这导致了基于MAP的主流SR重建方法。

1.3.4.2 最大后验

SR重建中的许多工作[46,84,15]遵循方程1.11中的MAP方法，其中技术随着不同的观察模型假设和用于期望解先验项Pr(X)而变化。在文献中已经提出了用于自然图像的不同种类的先验，但它们都没有突出作为主角。在下文中，我们列出了SR重建技术的三种常用图像先验。

  1. Gaussian MRF. 高斯马尔可夫随机场（GMRF）[37,33]采用以下形式

其中Q是对称正矩阵，通过其非对角线元素捕获图像中相邻像素之间的空间关系。Q通常被定义为ΓTΓ，其中Γ在图像X上充当一些一阶或二阶导数算子。在这种情况下，先验的对数似然性是

被大家熟知为Tikhonov正则化[95,26,63]，这是对不适定问题进行正则化的最常用方法。Γ通常称为Tikhonov矩阵。哈迪等人[35]提出了一种联合MAP框架，用于利用HR图像的高斯MRF先验同时估计高分辨率图像和运动参数。Bishop等人[96]提出了一种简单的高斯过程先验，其中协方差矩阵Q由图像像素的空间相关构成。高斯过程先验的良好分析性质允许对SR重建问题进行贝叶斯处理，其中未知高分辨率图像被整合出来用于观察模型参数（未知PSF和配准参数）的稳健估计。尽管GMRF先验具有许多分析优势，但与超分辨率重建相关的常见批评是结果往往过于平滑，惩罚了我们希望恢复的尖锐边缘。

  1. Huber MRF. 通过使用比高斯尾部更重的分布对图像梯度建模，GMRF的问题可以得到改善，这导致流行的Huber MRF（HMRF），其中Gibbs势由Huber函数确定，

其中a是图像的一阶导数。这样的先验可以促进分段平滑，并且可以很好地保留边缘。Schultz和Stevenson [83]将这个Huber MRF应用于单张影像扩展问题，后来应用于[84]中的SR重建问题。许多后来关于超分辨率的工作使用Huber MRF作为正则化先验，例如[11,12,15,13,73,74]和[3]。

  1. Total Variation. 作为梯度罚函数的总变差（TV）范数在图像去噪和去模糊文献中非常流行[81,54,16]。TV标准惩罚图像中的总变化量，如通过梯度大小的l1范数所测量的

其中∇是梯度算子，可以由拉普拉斯算子[81]近似。TV标准中的l1范数有利于稀疏梯度，保留陡峭的局部梯度，同时鼓励局部平滑[13]。Farsiu等人[30]概括了TV的符号，并提出了所谓的双边TV（BTV），以实现稳健的正规化。

为了更好地比较这些通用图像先验对超分辨率的解的影响，可以进一步参考[10]和[25]。

1.3.4.3 联合MAP恢复（Joint MAP restoration）

多帧SR重建可以分为两个子问题：LR配准和HR估计。许多先前的算法将这两个过程视为两个不同的过程：首先进行配准然后通过MAP进行估计，这是次优的，因为配准和估计是相互依赖的。如果允许它们之间的相互作用，则运动估计和HR估计可以彼此受益。 在联合MAP恢复中，等式1.11扩展到包括运动和PSF估计作为对于推理的未知数：

影像超分辨率：历史回顾和未来的挑战_第7张图片

Tom等人 [98]将SR问题分为三个子问题，即配准、恢复和插值。他们不是独立地解决它们，而是通过使用期望最大化（EM）最大化可能性来同时估计配准和恢复。后来他们在框架中插入了插值，并在[97]中估算了使用EM的所有未知数。 [35]应用MAP框架同时估计高分辨率图像和平移运动参数（PSF作为已知的先验）。使用循环坐标下降优化过程估计高分辨率图像和运动参数。该算法收敛缓慢但很大程度上改善了估计。Segall等人[86,85]提出了一种联合估计应用于压缩视频的密集运动矢量和HR图像的方法。Woods等人 [105]将噪声方差，正则化和配准参数都视为未知数，并根据可用的观测值在贝叶斯框架中联合估计它们。 Chung等人[19]提出了一个联合优化框架，并显示出优于坐标下降法的性能[46]。他们处理的运动模型是仿射变换。为了处理SR设置中更复杂的多个移动物体问题，Shen等人 [87]通过将运动估计、分割和SR重建结合在一起的MAP公式解决了这个问题。优化是在类似于[46]的循环坐标下降过程中完成的。

1.3.4.4 贝叶斯处理（Bayesian Treatments)

由于有限的低分辨率观察，SR重建问题本质上是不适定的。运动参数，PSF和HR图像的联合MAP估计可能面临过度拟合的问题[96]。虽然通常难以对运动和模糊进行建模，但在许多情况下，由少数参数跨越的简单模型足以用于SR应用。然而，给定了低分辨率观察，通过在未知高分辨率图像上积分来估计这些参数是有用的方法。 Bishop [96]为SR提出了这种贝叶斯方法，其中未知的高分辨率图像被整合出来，边缘用于估计PSF和运动参数。为了使问题在分析上易于处理，使用高斯过程先验（GMRF）来模拟高分辨率图像。即使将不利的GMRF用于高分辨率图像，仍然可以非常准确地估计PSF和运动参数。然后，估计的参数是固定的，并且执行HR图像的MAP估计。在[53]中讨论了类似于盲解卷积的深入分析。这种贝叶斯方法优于1.3.4.3中的联合MAP方法，该方法很容易过度拟合PSF参数。然而，高分辨率图像上的积分在计算上很繁重，并且图像上的高斯先验导致最终重建走向过度平滑。Pickup等人并没有对未知的高分辨率图像进行边缘化，而是在他们最近的作品[73,74,72]中提出要整合未知的PSF和运动参数，如公式1.8所示，其动机是克服注册参数的不确定性[79]。预先估计配准参数，然后将其作为高斯变量处理，其中预估值作为模拟其不确定性的手段。在对观测模型参数进行积分之后，可以将HR图像估计与用于MAP估计的任何有利图像组合。如[73,74,72]中所报道的，与[96]相比，这种方法可以获得更清晰的结果。

通过边缘化未知物进行的这种贝叶斯处理证明了SR恢复的有希望的能力。然而，为了使积分易于处理，图像先验或配准参数必须采用简单的参数形式，限制这些模型处理可能在真实视频中发生的更复杂的情况。在实际应用中，计算也可能是这种算法的关注点。

1.3.5 基于实例的方法（Example-based approach）

先前的超分辨率方法依赖于聚合包含互补空间信息的多个帧。通常部署通用图像先验以正确地正则化解。当提供的测量数量不足时，正则化变得尤其重要，因为在极端情况下，仅观察到一个单独的低分辨率帧。在这种情况下，通用图像先验不足以作为SR的有效正则化[2]。最近出现的用于使不适定的超分辨率重建正则化的方法是使用示例，以打破由不充分的测量引起的超分辨率限制。 与先前处于以整个图像正则化的参数形式的先前方法不同，基于示例的方法通过从其他图像采样来开发先验，类似于[24]，[38]以局部方式。

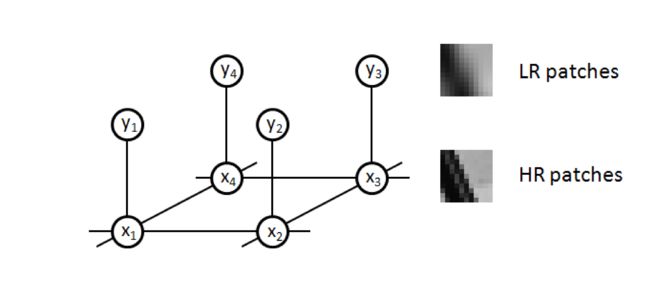
一系列基于实例的方法是直接使用这些实例，代表性工作是Freeman等人提出的[31]。这些方法通常通过维持两组training patches来工作，{xi}ni=1从高分辨率图像采样，并且{yi}ni=1相应地从低分辨率图像采样。每个patch对(xi, yi)通过观察模型yi = DHxi + v连接。然后将该高分辨率和低分辨率共生模型应用于目标图像，以基于patch的方式预测高分辨率图像，使用马尔可夫随机场（MRF）模型，如图1.5所示。观察模型参数必须已知为先验，并且训练集与目标图像紧密耦合。还应正确选择patch大小。如果patch尺寸非常小，则共生先验太弱而不能使预测有意义。另一方面，如果patch尺寸太大，则可能需要大量训练集来为当前观察找到接近的patch。

影像超分辨率：历史回顾和未来的挑战_第8张图片
图1.5 用于单帧超分辨率的MRF模型

使用这种耦合训练集进行超分辨率的一种单纯的方法是，对于低分辨率图像中的每个低分辨率patch，在{yi}ni=1中找到它的最近邻居y~，然后将相应的从{xi}ni=1得到的x~放置到高分辨率图像网格。不幸的是，由于噪声和超分辨率的不适定性，这种简单的方法会产生令人不安的伪像[25]。放宽最近邻搜索到k-最近邻居可以确保包括我们期望的接近patch。Freeman等人 [31]提出了一种基于上述MRF模型的置信传播[108]算法，以选择由k个最近邻居找到的最佳高分辨率补丁，其与临近patch具有最佳兼容性。Sun等人[90]使用sketch prior仅来增强图像中的边缘扩展了这个想法，旨在加速算法。然后将IBP [39]算法用作后处理步骤以确保整个图像上的数据一致性。Wang等人[103]进一步遵循这一工作，并提出了一个可以处理未知PSF的统计模型。

上述方法直接基于图像patch，需要大型训练集以包括测试中可能遇到的任何模式（pattern）。Chang等人[17] 提出了另一种基于邻居嵌入的简单但有效的方法[93]，假设由低分辨率和高分辨率图像patch形成的两个流形之间的对应关系。对于来自测试图像（上标“t”区分测试patch和训练patch）的每个低分辨率图像patch ytk，算法从{yi}ni=1找到其k个最近邻居Nt，并通过邻居嵌入计算重建权重

影像超分辨率：历史回顾和未来的挑战_第9张图片

然后应用重建权重以生成相应的高分辨率patch。

影像超分辨率：历史回顾和未来的挑战_第10张图片
为了处理相邻patch之间的兼容性问题，在重叠区域中执行简单平均。即使使用比[108]更小的patch数据库，该算法也能很好地工作。但是，为每个低分辨率patch修复k可能会导致过度拟合或欠拟合。 Yang等人[107]提出了另一种基于patch的单帧超分辨率方法。该方法源于压缩传感理论，该理论确保高分辨率信号之间的线性关系可以从其低维投影中精确恢复[9], [22]。该算法将训练集建模为两个字典： D h = [ x 1, x 2, ..., x n]和 D l = [ y 1, y 2, ..., y n]。给定测试低分辨率图像patch y t k，该方法基本上通过l1最小化来寻求支持[23]

这可以用拉格朗日乘数重写为统计文献中称为Lasso的无约束优化问题[94]。通过xtk = Dhw^恢复相应的高分辨率patch。与具有固定k个邻居的邻居嵌入方法相比，Yang的方法自适应地选择最少的必要重建支持，避免过度拟合。此外，与前面提到的基于patch的方法相比，l1最小化方法对噪声更稳健。在后来的版本[42]中，通过学习耦合字典而不是使用原始patch来进一步扩展该方法，从而使算法更有效。

使用直接示例的前述方法的一个批评是对局部patch的操作不能保证估计的全局最优性。另一种基于示例的方法寻求在从示例采样的图像空间上利用局部先验执行MAP估计。Baker和Kanade [2]的开创性工作制定了明确的正则化，要求未知图像的空间导数与找到的例子的空间导数相近。这些示例由金字塔衍生的特征组（a pyramid derivative set of features）形成，而不是直接由原始数据生成。类似的方法应用于[75]中的文本超分辨率。Datsenko和Elad [21]提出了一种全局MAP估计，其中基于实例的正则化由二进制加权平均而不是最近邻居给出，绕过由于噪声引起的异常值。这项工作在[21]中进一步扩展和阐述，其中放宽了二进制加权方案。基于实例的方法的另一个值得注意的方法是Protter等人[78]，从非局部均值去噪算法[8]推广。算法不是从其他训练图像中采样，而是探索图像（或序列）中的自相似性，并从目标图像（或序列）本身中提取示例块。Glasner等人最近的一项工作通过结合基于子像素位移的经典算法和基于从目标图像提取的patch对的基于实例的方法，进一步探索了SR图像中的自相似性。

在处理狭窄的图像族（例如文本和面部图像）时，使用示例可以更加有效。由于其在监视场景中的重要性，近年来出现了一组针对面部超分辨率的算法。在Baker和Kanade的早期工作之后，面部超分辨率通常被称为面部幻觉（face hallucination）[2]。Capel等人[14]提出了一种算法，其中PCA [45]子空间模型用于学习面部的部分。Liu等人[58]，[57]提出了一种两步法来实现面部的超分辨率，其中第一步使用特征脸（eigenface）[100]生成中等分辨率面部，然后是非参数基于patch的方法[31]在第二步。这种基于特征脸的方法已经在后来的几个作品[32]，[104]中进行了探索。Yang等人[106]提出了类似的两步法。[106]不使用整体PCA子空间，而是使用局部非负矩阵分解（NMF）[51]来模拟人脸，第二步中基于patch的模型从[107]中采用。Jia和Gong [43]，[44]提出了张量方法来处理更多的面部变化，例如照明和表情。尽管这些面部幻觉算法的效果令人惊讶，但它们仅适用于正面，并且只有少数作品专门用于评估面部幻觉以进行识别[32]，[36]。

当观测资料不足时，基于实例的正则化在我们的SR问题中是有效的。关于这种方法，我们仍然需要回答一些问题。首先，如何在给定目标图像的情况下选择最佳补丁大小。也许需要多分辨率处理。第二，如何选择数据库。不同的图像具有不同的统计，因此需要不同的数据库。用于对当前目标图像进行字典适应的有效方法可以提出一种出路。第三，如何更有效地使用基于示例的先验。计算问题可能是实际应用的难点。建议读者参考[25]，对逆问题的基于实例的正则化进行更详细的分析。

1.3.6 集合理论重建（Set theoretic restoration）

除了如上所述从随机视图导出的优化方法之外，另一种方法流是通过众所周知的凸集投影（POCS）[110]。POCS方法通过将包含期望图像的多个约束凸集合作为集合内的点来处理SR问题。定义这样的凸集是灵活的，并且可以包含不同种类的约束或先验，甚至非线性和非参数约束。作为一个例子，我们在POCS方法中介绍了几种常用的凸集。数据一致性或重建约束可以建模为K凸集：

平滑约束可以定义为

其中p = 1, 2, ∞表示不同的范数。振幅约束也可以建模：

对于一组M个凸集，期望的解决方案在于这些集合的交集X∈Cs = ∩i = 1M Ci。POCS技术建议使用以下递归算法在给定初始猜测的情况下在交集中找到一个点：

其中X0是初始猜测，Pi是投射算子，它将点投射到闭合的凸集Ci上。

Stark等人提出了用于SR重建的早期POCS技术[88]。在[68], [67], [69]中提出扩展来处理空间变化的PSF，运动模糊，传感器模糊和混叠采样效应。许多超分辨率工作仅考虑非零光圈尺寸（镜头模糊，PSF），而不是有限光圈时间（运动模糊），这在真实的低分辨率视频中非常常见。[69]是基于POCS技术考虑视频SR重建中运动模糊的早期工作。由于由有限光圈时间引起的运动模糊通常将是空间变化，也可能是时变的，因此不能将其从SR恢复问题中分解出来并且作为单独的后处理步骤来执行。POCS技术可以方便地处理这些问题。延伸这种方法，Eren等人[28]提出了一种基于POCS的方法，用于稳健的基于对象的SR重建。所提出的方法采用有效性映射来基于具有不准确的运动估计的观察来禁用投影，以及用于基于对象的处理的分割图。 Elad等人[26]分析并比较了ML，MAP和POCS方法的超分辨率，并提出了一种混合方法。Patti [66]扩展了他们在图像观察模型中的早期工作，以允许高阶插值和修改的约束集来减少边缘振铃伪像。

POCS技术的优点在于其简单性可以包含任何类型的约束和先验，这些约束和先验可能对于那些随机方法而言是不可能的。然而，POCS因其繁重的计算和缓慢的收敛而臭名昭着。根据最初的猜测，解决方案并不是唯一的。POCS方法还假设运动参数和系统模糊。它们不能像随机方法同时估计那些配准参数和高分辨率图像。结合随机视图和POCS哲学的混合方法提出了一种有前景的方法。

1.4 超分辨率的挑战问题

在前面的章节中，我们讨论了SR重建的几种基本技术。尽管自引入SR概念以来已经提出了许多不同的方法，但大多数方法在小数据（toy data）上而不是在实际问题中工作得很好。在构建实用的SR系统时，仍然存在许多挑战问题，这些问题阻碍了SR技术的广泛应用。在下文中，我们列出了一些我们认为对SR技术的未来发展和应用很重要的挑战问题。

1.4.1 图像配准

图像配准对于多帧SR重建的成功至关重要，其中融合了HR图像的互补空间采样。图像配准是一个众所周知的不适定的基本图像处理问题。在SR设置中问题更加困难，其中观察是具有大的混叠伪像的低分辨率图像。随着观察的分辨率下降，标准图像配准算法的性能降低，导致更多的配准误差。由这些配准误差引起的伪像在视觉上比由单个图像的插值产生的模糊效果更令人讨厌。传统的SR重建通常将图像配准视为与HR图像估计不同的过程。因此，恢复的HR图像质量在很大程度上取决于前一步骤的图像配准精度。在文献[7,114]中已经提出了许多源自不同原理的图像配准技术。但是，罗宾逊等人[79]表明，即使对于最简单的全局平移，配准表现也是有限的。

LR图像配准和HR图像估计实际上是相互依赖的[80]。一方面，准确的子像素运动估计有益于HR图像估计。另一方面，高质量的HR图像可以促进精确的运动估计。因此，针对SR重建问题，LR图像配准可以与HR图像重建一起被处理，从而得到用于同时估计的联合ML [97]或​​MAP [35,87,76]框架。这些联合估计算法捕获LR图像配准和HR图像估计之间的依赖性，并且观察到性能改进。然而，在观察有限的情况下，对配准参数和HR图像的联合估计可能导致过度拟合。为了克服这种过度拟合问题，Tipping和Bishop [96]采用贝叶斯方法通过边缘化未知高分辨率图像来估计配准和模糊参数。该算法对于配准和模糊参数都显示出值得注意的估计精度，但是计算成本非常高。Pickup等人 [73,74,72]反而通过边缘化未知的配准参数以另一种方式应用贝叶斯方法，以解决图像配准固有的不确定性[79]。

将HR图像估计与图像配准相关联的随机方法确实展示了有希望的结果，然而这种参数方法在它们可以有效处理的运动模型中受到限制。通常，假设一些简单的全局运动模型。真实视频是复杂的，包括任意局部运动，其中运动模型的参数化可能是难以处理的。光流运动估计可以应用于这种情况。然而，局部运动估计的测量不足使得这些算法容易出错，这可能导致SR重建的灾难[112]。另一种有希望的SR重建方法是非参数方法，它试图绕过显式运动估计。Protter等[78]将非局部均值去噪算法扩展到SR重建，其中使用了基于块匹配的模糊运动估计。后来他们在[77]中提出了概率运动模型，这是一个类比[72]的非参数模型。 [78]和[77]都可以处理真实视频中的复杂运动模式。与基于光流运动估计的经典SR方法相比，Protter的方法通过在多个可能的候选者上的加权策略减少由未对准引起的误差。Takeda等人[92]，另一方面，将早期工作[91]中提出的3-D转向核应用于视频，这也避免了显式运动估计，用于去噪和SR重建。3-D转向核捕获空间和时间结构，编码隐式运动信息，因此可以应用于具有复杂运动活动的视频的空间和时间SR。虽然没有显式运动估计的方法确实产生了对于SR技术的实际适用性的有希望的结果，但是进一步的改进可以包括计算效率，将自适应插值或回归与去模糊相结合，并且将观察模型泛化至视频中的3-D运动，例如，面外旋转。

1.4.4 计算效率

限制SR重建的实际应用的另一个难点是由于大量未知数而导致的密集计算，这需要昂贵的矩阵操作。实际应用总是要求SR重建的效率以具有实用性，例如，在监视视频场景中，人们期望SR重建是实时的。对于具有用户参与调整参数的SR系统，效率也是期望的。许多针对效率的SR算法属于先前讨论的插值恢复方法，例如[27], [1], [61]和[34]。在[34]中，Hardie展示了他的算法优于[1]和[61]中提出的先前有效算法的计算优势，并声称该算法可以与全局平移模型实时应用。然而，当非平移模型发生时，计算显着增加，这可以通过大规模并行计算来改善。其他人试图检查特定的建模方案以加速优化问题。Zomet [115]和Farsiu [30]直接研究了Dk，Hk和Fk的应用，作为下采样、模糊和移位的相应图像操作，绕过了明确构造矩阵的需要，带来了显着的加速。[6]结合了[27]和[30]的略微修改版本，并使用FPGA实现了实时SR系统，这是对SR实际使用的一种很好的尝试。

然而，这种算法需要精确的图像配准，这首先是计算密集型的。而且，这些算法到目前为止只能有效地处理简单的运动模型，远非真实复杂视频场景中的应用。对于具有任意运动的视频，[92]提出了寻求有效算法的有希望的方向。看到并行计算（例如GPU）和硬件实现如何影响SR技术的未来应用也是有趣的。

1.4.3 稳健性方面

由于运动误差、不准确的模糊模型、噪声、运动物体、运动模糊等，传统的SR技术容易受到异常值的影响。这些不准确的模型误差不能像高斯噪声一样被视为具有l2重建残差的通常假设。SR的稳健性是令人感兴趣的，因为不能完美地估计图像劣化模型参数，并且对异常值的敏感性可能导致视觉上令人不安的伪像，这在许多应用中是不可容忍的，例如视频标准转换。但是，没有足够的工作专注于这样一个重要方面。 Chiang和Boulte[18]使用中值估计来组合上采样图像以应对来自非平稳噪声的异常值。Zomet等人[116]以不同的方式抛出问题，其中使用稳健的基于中值的梯度进行优化以绕过异常值的影响。Farsiu等人[30], [82]将常用的“l2范数”改为“l1范数，用于类似于[18]的鲁棒估计和稳健正则化。[113]引入了同时具有Huber范数的超分辨率作为鲁棒正则化的先验。Pham等人[71]通过在双边滤波中使用相同的基于光度的加权方案，为每个相邻样本提出了用于内插未知数据的鲁棒确定性。在概率运动模型[77]中也使用类似的不确定性方案来处理基于块匹配的光流运动估计误差。这些算法中的许多都显示出对小数据假定的异常值的改进，其中需要更多的实验评估来确定稳健性努力可以使真实SR性能受益多少。

1.4.4 性能限制

SR重建自引入以来已成为一个热门的研究课题，成千上万的SR论文已经发展成为出版物。然而，没有太多的工作致力于基本理解这些SR重建算法的性能极限。这种性能限制的理解很重要。例如，它将阐明SR摄像机的设计，有助于分析模型误差、缩放因子和帧数等因素。通常，对所有SR技术的性能限制进行雄心勃勃的分析可能是难以处理的。首先，SR重建是一项复杂的任务，由许多相互依赖的组成部分组成。其次，对于SR任务，特别是对于基于实例的方法，仍然不知道什么是最具信息性的先验。最后，性能评估仍然需要一个很好的衡量而不是简单的MSE。已经认识到，具有较高MSE的估计不一定在视觉上更具吸引力。例如，与通过一些基于实例的方法恢复的那些相比，双三次插值通常实现更小的MSE [107]。

在过去的几年中，已经提出了几种尝试理解性能的作品。[2]分析了SR线性系统的数值条件，并得出结论，随着变焦因子的增加，一般图像先验对SR的帮助越来越少。[56]基于矩阵扰动导出了性能限制，但假设图像配准作为先验。使用简单的平移模型，Robinson和Milanfar在[79]中使用Cram'er-Rao（CR）界限来分析配准性能限制。他们在[80]中扩展了这项工作，通过运动估计、抽取因子、帧数和先验信息等因素对SR性能进行了全面分析。该分析基于MSE标准，并且再次假设运动模型是简单的全局变换。Eekeren等[102]评估了几种实际数据的SR算法，根据经验探索了几个影响因素。虽然这些关于理解性能限制的努力对于SR来说远远不够，但它们确实提出了让人们遵循的方法。

虽然很难为不同的SR技术得出一致的结论，但在性能评估方面，需要一些基准和现实的数据集来进行公平比较和算法理解。未来的研究应该进行更多的理论分析和绩效评估，以指导SR技术的发展。

你可能感兴趣的:(影像超分辨率：历史回顾和未来的挑战)

  • 斤斤计较的婚姻到底有多难？ 白心之岂必有为
    很多人私聊我会问到在哪个人群当中斤斤计较的人最多？我都会回答他，一般婚姻出现问题的斤斤计较的人士会非常多，以我多年经验，在婚姻落的一塌糊涂的人当中，斤斤计较的人数占比在20～30%以上，也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中，有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型：第一种是物质上的，另一种是精神上的。在物质与精神上抠门已经严重的影响
  • 情绪觉察日记第37天 露露_e800
    今天是家庭关系规划师的第二阶最后一天，慧萍老师帮我做了个案，帮我处理了埋在心底好多年的一份恐惧，并给了我深深的力量！这几天出来学习，爸妈过来婆家帮我带小孩，妈妈出于爱帮我收拾东西，并跟我先生和婆婆产生矛盾，妈妈觉得他们没有照顾好我…。今晚回家见到妈妈，我很欣赏她并赞扬她，妈妈说今晚要跟我睡我说好，当我们俩躺在床上准备睡觉的时候，我握着妈妈的手对她说:妈妈这几天辛苦你了，你看你多利害把我们的家收拾得
  • 芦花鞋一四 许叶晗
    又是在一个寒冷的夏日里，青铜和葵花决定今天一起去卖芦花鞋，奶奶亲手给他们做了一碗热乎乎的粥对他们说:“就靠你们两挣生活费了这碗粥赶紧趁热喝了吧！”于是青铜和葵花喝完了奶奶给她们做的粥，就准备去镇上卖卢花鞋，这回青铜和葵花穿着新的芦花鞋来到了镇上。青铜这回看到了很多人都在卖，用手势表达对葵花说:“这回有好多人在抢我们生意呢！我们必须得吆喝起来。”葵花点了点头。可是谁知他们也大声的叫，卖芦花喽！卖芦花
  • QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
    功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
  • 关于沟通这件事，项目经理不需要每次都面对面进行 流程大师兄
    很多项目经理都会遇到这样的问题，项目中由于事情太多，根本没有足够的时间去召开会议，那在这种情况下如何去有效地管理项目中的利益相关者？当然，不建议电子邮件也不需要开会的话，建议可以采取下面几种方式来形成有效的沟通，这几种方式可以帮助你努力的通过各种办法来保持和各方面的联系。项目经理首先要问自己几个问题，项目中哪些利益相关者是必须要进行沟通的？可以列出项目中所有的利益相关者清单，同时也整理出项目中哪些
  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 铭刻于星（四十二） 随风至
    69夜晚，绍敏同学做完功课后，看了眼房外，没听到动静才敢从书包的夹层里拿出那个心形纸团。折痕压得很深，都有些旧了，想来是已经写好很久了。绍敏同学慢慢地、轻轻地捏开折叠处，待到全部拆开后，又反复抚平纸张，然后仔细地一字字默看。只是开头的三个字是第一次看到，让她心漏跳了几拍。“亲爱的绍敏：从四年级的时候，我就喜欢你了，但是我一直不敢说，怕影响你学习。六年级的时候听说有人跟你表白，你接受了，我很难过，但
  • 底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说 造命者说
    底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说我叫吴起，生于公元前440年的战国初期，正是群雄并起、天下纷争不断的时候。后人说我是军事家、政治家、改革家，是兵家代表人物。评价我一生历仕鲁、魏、楚三国，通晓兵家、法家、儒家三家思想，在内政军事上都有极高的成就。周安王二十一年（公元前381年），因变法得罪守旧贵族，被人乱箭射死。我出生在卫国一个“家累万金”的富有家庭，从年轻时候起就不甘平凡
  • 2020-01-25 晴岚85
    郑海燕坚持分享590天2020.1.24在生活中只存在两个问题。一个问题是：你知道想要达成的目标是什么，但却不知道如何才能达成；另一个问题是：你不知道你的目标是什么。前一个是行动的问题，后一个是结果的问题。通过制定具体的下一步行动，可以解决不知道如何开始行动的问题。而通过去想象结果，对结果做预估，可以解决找不着目标的问题。对于所有吸引我们注意力，想要完成的任务，你可以先想象一下，预期的结果究竟是什
  • 随笔 | 仙一般的灵气 海思沧海
    仙岛今天，我看了你全部，似乎已经进入你的世界我不知道，这是否是梦幻，还是你仙一般的灵气吸引了我也许每一个人都要有一份属于自己的追求，这样才能够符合人生的梦想，生活才能够充满着阳光与快乐我不知道，我为什么会这样的感叹，是在感叹自己的人生，还是感叹自己一直没有孜孜不倦的追求只感觉虚度了光阴，每天活在自己的梦中，活在一个不真实的世界是在逃避自己，还是在逃避周围的一切有时候我嘲笑自己，嘲笑自己如此的虚无，
  • 想家 爆米花机
    也许不同于大家对家乡的思念，我对家乡甚至是疯狂的不舍。还未踏出车站就感觉到幸福，我享受这里的夕阳、这里的浓烈柴火味、这里每一口家常菜。我是宅女，我贪恋家的安逸。刚刚踏出大学校门，初出茅庐，无法适应每年只能国庆和春节回家。我焦虑、失眠、无端发脾气，是无法适应工作的节奏，是无法接受我将一步步离开家乡的事实。我不想承认自己胸无大志，选择再次踏上征程。图片发自App
  • 【iOS】MVC设计模式 Magnetic_h iosmvc设计模式objective-c学习ui
    MVC前言如何设计一个程序的结构，这是一门专门的学问，叫做"架构模式"（architecturalpattern），属于编程的方法论。MVC模式就是架构模式的一种。它是Apple官方推荐的App开发架构，也是一般开发者最先遇到、最经典的架构。MVC各层controller层Controller/ViewController/VC（控制器）负责协调Model和View，处理大部分逻辑它将数据从Mod
  • OC语言多界面传值五大方式 Magnetic_h iosui学习objective-c开发语言
    前言在完成暑假仿写项目时，遇到了许多需要用到多界面传值的地方，这篇博客来总结一下比较常用的五种多界面传值的方式。属性传值属性传值一般用前一个界面向后一个界面传值，简单地说就是通过访问后一个视图控制器的属性来为它赋值，通过这个属性来做到从前一个界面向后一个界面传值。首先在后一个界面中定义属性@interfaceBViewController:UIViewController@propertyNSSt
  • 一百九十四章. 自相矛盾 巨木擎天
    唉！就这么一夜，林子感觉就像过了很多天似的，先是回了阳间家里，遇到了那么多不可思议的事情儿。特别是小伙伴们，第二次与自己见面时，僵硬的表情和恐怖的气氛，让自己如坐针毡，打从心眼里难受！还有东子，他现在还好吗？有没有被人欺负？护城河里的小鱼小虾们，还都在吗？水不会真的干枯了吧？那对相亲相爱漂亮的太平鸟儿，还好吧！春天了，到了做窝、下蛋、喂养小鸟宝宝的时候了，希望它们都能够平安啊！虽然没有看见家人，也
  • UI学习——cell的复用和自定义cell Magnetic_h ui学习
    目录cell的复用手动（非注册）自动（注册）自定义cellcell的复用在iOS开发中，单元格复用是一种提高表格（UITableView）和集合视图（UICollectionView）滚动性能的技术。当一个UITableViewCell或UICollectionViewCell首次需要显示时，如果没有可复用的单元格，则视图会创建一个新的单元格。一旦这个单元格滚动出屏幕，它就不会被销毁。相反，它被添
  • element实现动态路由+面包屑 软件技术NINI vue案例vue.js前端
    el-breadcrumb是ElementUI组件库中的一个面包屑导航组件，它用于显示当前页面的路径，帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中，如果你已经安装了ElementUI，就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例：安装ElementUI（如果你还没有安装的话）:你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
  • 10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
    本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
  • C语言宏函数 南林yan C语言c语言
    一、什么是宏函数？通过宏定义的函数是宏函数。如下，编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
  • 地推话术，如何应对地推过程中家长的拒绝 校师学
    相信校长们在做地推的时候经常遇到这种情况：市场专员反馈家长不接单，咨询师反馈难以邀约这些家长上门，校区地推疲软，招生难。为什么？仅从地推层面分析，一方面因为家长受到的信息轰炸越来越多，对信息越来越“免疫”；而另一方面地推人员的专业能力和营销话术没有提高，无法应对家长的拒绝，对有意向的家长也不知如何跟进，眼睁睁看着家长走远；对于家长的疑问，更不知道如何有技巧地回答，机会白白流失。由于回答没技巧和专业
  • 谢谢你们，爱你们！ 鹿游儿
    昨天家人去泡温泉，二个孩子也带着去，出发前一晚，匆匆下班，赶回家和孩子一起收拾。饭后，我拿出笔和本子（上次去澳门时做手帐的本子）写下了1\2\3\4\5\6\7\8\9,让后让小壹去思考，带什么出发去旅游呢？她在对应的数字旁边画上了，泳衣、泳圈、肖恩、内衣内裤、tapuy、拖鞋……画完后，就让她自己对着这个本子，将要带的，一一带上，没想到这次带的书还是这本《便便工厂》(晚上姑婆发照片过来，妹妹累得
  • C语言如何定义宏函数？ 小九格物 c语言
    在C语言中，宏函数是通过预处理器定义的，它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为，但它们不是真正的函数，因为它们在编译时不会进行类型检查，也不会分配存储空间。宏函数的定义通常使用#define指令，后面跟着宏的名称和参数列表，以及宏展开后的代码。宏函数的定义方式：1.基本宏函数：这是最简单的宏函数形式，它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
  • 微服务下功能权限与数据权限的设计与实现 nbsaas-boot 微服务java架构
    在微服务架构下，系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加，如何保证不同用户和服务之间的访问权限准确、细粒度地控制，成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限：指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作，比如查看订单、创建订单、修改用户资料等。数据权限：
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • 小丽成长记（四十三） 玲玲54321
    小丽发现，即使她好不容易调整好自己的心态下一秒总会有不确定的伤脑筋的事出现，一个接一个的问题，人生就没有停下的时候，小问题不断出现。不过她今天看的书，她接受了人生就是不确定的，厉害的人就是不断创造确定性，在Ta的领域比别人多的确定性就能让自己脱颖而出，显示价值从而获得的比别人多的利益。正是这样的原因，因为从前修炼自己太少，使得她现在在人生道路上打怪起来困难重重，她似乎永远摆脱不了那种无力感，有种习
  • 学点心理知识，呵护孩子健康 静候花开_7090
    昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
  • 2021年12月19日，春蕾教育集团团建活动感受——黄晓丹 黄错错加油
    感受:1.从陌生到熟悉的过程。游戏环节让我们在轻松的氛围中得到了锻炼，也增长了不少知识。2.游戏过程中，我们贡献的是个人力量，展现的是团队的力量。它磨合的往往不止是工作的熟悉，更是观念上契合度的贴近。3.这和工作是一样的道理。在各自的岗位上，每个人摆正自己的位置、各司其职充分发挥才能，并团结一致劲往一处使，才能实现最大的成功。新知:1.团队精神需要不断地创新。过去，人们把创新看作是冒风险，现在人们
  • Cell Insight | 单细胞测序技术又一新发现，可用于HIV-1和Mtb共感染个体诊断 尐尐呅
    结核病是艾滋病合并其他疾病中导致患者死亡的主要原因。其中结核病由结核分枝杆菌（Mycobacteriumtuberculosis,Mtb）感染引起，获得性免疫缺陷综合症（艾滋病）由人免疫缺陷病毒（Humanimmunodeficiencyvirustype1,HIV-1）感染引起。国家感染性疾病临床医学研究中心/深圳市第三人民医院张国良团队携手深圳华大生命科学研究院吴靓团队，共同研究得出单细胞测序
  • c++ 的iostream 和 c++的stdio的区别和联系 黄卷青灯77 c++算法开发语言iostreamstdio
    在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
  • 瑶池防线 谜影梦蝶
    冥华虽然逃过了影梦的军队，但他是一个忠臣，他选择上报战况。败给影梦后成逃兵，高层亡尔还活着，七重天失守......随便一条，即可处死冥华。冥华自然是知道以仙界高层的习性此信一发自己必死无疑，但他还选择上报实情，因为责任。同样此信送到仙宫后，知道此事的人，大多数人都认定冥华要完了，所以上到仙界高层，下到扫大街的，包括冥华自己，全都准备好迎接冥华之死。如果仙界现在还属于两方之争的话，冥华必死无疑。然而
  • 爬山后遗症 璃绛
    爬山，攀登，一步一步走向制高点，是一种挑战。成功抵达是一种无法言语的快乐，在山顶吹吹风，看看风景，这是从未有过的体验。然而，爬山一时爽，下山腿打颤，颠簸的路，一路向下走，腿部力量不够，走起来抖到不行，停不下来了！第二天必定腿疼，浑身酸痛，坐立难安！
  • ztree设置禁用节点 3213213333332132 JavaScriptztreejsonsetDisabledNodeAjax
    ztree设置禁用节点的时候注意，当使用ajax后台请求数据,必须要设置为同步获取数据，否者会获取不到节点对象，导致设置禁用没有效果。 $(function(){ showTree(); setDisabledNode(); });
  • JVM patch by Taobao bookjovi javaHotSpot
    在网上无意中看到淘宝提交的hotspot patch，共四个，有意思，记录一下。   7050685：jsdbproc64.sh has a typo in the package name 7058036：FieldsAllocationStyle=2 does not work in 32-bit VM 7060619：C1 should respect inline and
  • 将session存储到数据库中 dcj3sjt126com sqlPHPsession
    CREATE TABLE sessions ( id CHAR(32) NOT NULL, data TEXT, last_accessed TIMESTAMP NOT NULL, PRIMARY KEY (id) );   <?php /** * Created by PhpStorm. * User: michaeldu * Date
  • Vector 171815164 vector
    public Vector<CartProduct> delCart(Vector<CartProduct> cart, String id) { for (int i = 0; i < cart.size(); i++) { if (cart.get(i).getId().equals(id)) { cart.remove(i);
  • 各连接池配置参数比较 g21121 连接池
            排版真心费劲，大家凑合看下吧，见谅~     Druid DBCP C3P0 Proxool 数据库用户名称 Username Username User   数据库密码 Password Password Password   驱动名
  • [简单]mybatis insert语句添加动态字段 53873039oycg mybatis
          mysql数据库,id自增,配置如下：       <insert id="saveTestTb" useGeneratedKeys="true" keyProperty="id" parameterType=&
  • struts2拦截器配置 云端月影 struts2拦截器
    struts2拦截器interceptor的三种配置方法 方法1. 普通配置法 <struts>     <package name="struts2" extends="struts-default">         &
  • IE中页面不居中，火狐谷歌等正常 aijuans IE中页面不居中
    问题是首页在火狐、谷歌、所有IE中正常显示，列表页的页面在火狐谷歌中正常，在IE6、7、8中都不中，觉得可能那个地方设置的让IE系列都不认识，仔细查看后发现，列表页中没写HTML模板部分没有添加DTD定义，就是<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3
  • String,int,Integer,char 几个类型常见转换 antonyup_2006 htmlsql.net
    如何将字串 String 转换成整数 int? int i = Integer.valueOf(my_str).intValue(); int i=Integer.parseInt(str); 如何将字串 String 转换成Integer ? Integer integer=Integer.valueOf(str); 如何将整数 int 转换成字串 String ? 1.
  • PL/SQL的游标类型 百合不是茶 显示游标(静态游标)隐式游标游标的更新和删除%rowtyperef游标(动态游标)
    游标是oracle中的一个结果集,用于存放查询的结果;   PL/SQL中游标的声明; 1,声明游标 2,打开游标(默认是关闭的); 3,提取数据 4,关闭游标     注意的要点:游标必须声明在declare中,使用open打开游标,fetch取游标中的数据,close关闭游标   隐式游标:主要是对DML数据的操作隐
  • JUnit4中@AfterClass @BeforeClass @after @before的区别对比 bijian1013 JUnit4单元测试
    一.基础知识 JUnit4使用Java5中的注解（annotation），以下是JUnit4常用的几个annotation： @Before：初始化方法   对于每一个测试方法都要执行一次（注意与BeforeClass区别，后者是对于所有方法执行一次）@After：释放资源  对于每一个测试方法都要执行一次（注意与AfterClass区别，后者是对于所有方法执行一次
  • 精通Oracle10编程SQL(12)开发包 bijian1013 oracle数据库plsql
    /* *开发包 *包用于逻辑组合相关的PL/SQL类型（例如TABLE类型和RECORD类型）、PL/SQL项（例如游标和游标变量）和PL/SQL子程序（例如过程和函数） */ --包用于逻辑组合相关的PL/SQL类型、项和子程序，它由包规范和包体两部分组成 --建立包规范：包规范实际是包与应用程序之间的接口，它用于定义包的公用组件，包括常量、变量、游标、过程和函数等 --在包规
  • 【EhCache二】ehcache.xml配置详解 bit1129 ehcache.xml
    在ehcache官网上找了多次，终于找到ehcache.xml配置元素和属性的含义说明文档了，这个文档包含在ehcache.xml的注释中！ ehcache.xml ： http://ehcache.org/ehcache.xml ehcache.xsd ： http://ehcache.org/ehcache.xsd ehcache配置文件的根元素是ehcahe   ehcac
  • java.lang.ClassNotFoundException: org.springframework.web.context.ContextLoaderL 白糖_ javaeclipsespringtomcatWeb
    今天学习spring+cxf的时候遇到一个问题：在web.xml中配置了spring的上下文监听器： <listener> <listener-class>org.springframework.web.context.ContextLoaderListener</listener-class> </listener>  随后启动
  • angular.element boyitech AngularJSAngularJS APIangular.element
    angular.element 描述:     包裹着一部分DOM element或者是HTML字符串，把它作为一个jQuery元素来处理。（类似于jQuery的选择器啦）     如果jQuery被引入了，则angular.element就可以看作是jQuery选择器，选择的对象可以使用jQuery的函数；如果jQuery不可用，angular.e
  • java-给定两个已排序序列，找出共同的元素。 bylijinnan java
    import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class CommonItemInTwoSortedArray { /** * 题目：给定两个已排序序列，找出共同的元素。 * 1.定义两个指针分别指向序列的开始。 * 如果指向的两个元素
  • sftp 异常，有遇到的吗？求解 Chen.H javajcraftauthjschjschexception
    com.jcraft.jsch.JSchException: Auth cancel at com.jcraft.jsch.Session.connect(Session.java:460) at com.jcraft.jsch.Session.connect(Session.java:154) at cn.vivame.util.ftp.SftpServerAccess.connec
  • [生物智能与人工智能]神经元中的电化学结构代表什么? comsci 人工智能
         我这里做一个大胆的猜想,生物神经网络中的神经元中包含着一些化学和类似电路的结构,这些结构通常用来扮演类似我们在拓扑分析系统中的节点嵌入方程一样,使得我们的神经网络产生智能判断的能力,而这些嵌入到节点中的方程同时也扮演着"经验"的角色....      我们可以尝试一下...在某些神经
  • 通过LAC和CID获取经纬度信息 dai_lm laccid
    方法1： 用浏览器打开http://www.minigps.net/cellsearch.html，然后输入lac和cid信息(mcc和mnc可以填0)，如果数据正确就可以获得相应的经纬度 方法2： 发送HTTP请求到http://www.open-electronics.org/celltrack/cell.php?hex=0&lac=<lac>&cid=&
  • JAVA的困难分析 datamachine java
    前段时间转了一篇SQL的文章（http://datamachine.iteye.com/blog/1971896），文章不复杂，但思想深刻，就顺便思考了一下java的不足，当砖头丢出来，希望引点和田玉。   -----------------------------------------------------------------------------------------
  • 小学5年级英语单词背诵第二课 dcj3sjt126com englishword
    money 钱 paper 纸 speak 讲，说 tell 告诉   remember 记得，想起 knock 敲，击，打 question 问题 number 数字，号码   learn 学会，学习 street 街道 carry 搬运，携带 send 发送，邮寄，发射   must 必须 light 灯，光线，轻的 front
  • linux下面没有tree命令 dcj3sjt126com linux
    centos p安装 yum -y install tree   mac os安装 brew install tree   首先来看tree的用法 tree 中文解释：tree 功能说明：以树状图列出目录的内容。 语　　法：tree [-aACdDfFgilnNpqstux][-I <范本样式>][-P <范本样式
  • Map迭代方式，Map迭代，Map循环 蕃薯耀 Map循环Map迭代Map迭代方式
    Map迭代方式，Map迭代，Map循环   >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年
  • Spring Cache注解+Redis hanqunfeng spring
    Spring3.1 Cache注解  依赖jar包： <!-- redis --> <dependency> <groupId>org.springframework.data</groupId> <artifactId>spring-data-redis</artifactId>
  • Guava中针对集合的 filter和过滤功能 jackyrong filter
    在guava库中，自带了过滤器(filter)的功能，可以用来对collection 进行过滤，先看例子：    @Test public void whenFilterWithIterables_thenFiltered() { List<String> names = Lists.newArrayList("John"
  • 学习编程那点事 lampcy 编程androidPHPhtml5
    一年前的夏天，我还在纠结要不要改行，要不要去学php？能学到真本事吗？改行能成功吗？太多的问题，我终于不顾一切，下定决心，辞去了工作，来到传说中的帝都。老师给的乘车方式还算有效，很顺利的就到了学校，赶巧了，正好学校搬到了新校区。先安顿了下来，过了个轻松的周末，第一次到帝都，逛逛吧！ 接下来的周一，是我噩梦的开始，学习内容对我这个零基础的人来说，除了勉强完成老师布置的作业外，我已经没有时间和精力去
  • 架构师之流处理---------bytebuffer的mark,limit和flip nannan408 ByteBuffer
    1.前言。   如题，limit其实就是可以读取的字节长度的意思，flip是清空的意思，mark是标记的意思 。 2.例子. 例子代码: String str = "helloWorld"; ByteBuffer buff = ByteBuffer.wrap(str.getBytes()); Sy
  • org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1, column 1 Everyday都不同 $转义el表达式
    最近在做Highcharts的过程中，在写js时，出现了以下异常：   严重: Servlet.service() for servlet jsp threw exception org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1,
  • 用Java实现发送邮件到163 tntxia java实现
    /* 在java版经常看到有人问如何用javamail发送邮件？如何接收邮件？如何访问多个文件夹等。问题零散，而历史的回复早已经淹没在问题的海洋之中。 本人之前所做过一个java项目，其中包含有WebMail功能，当初为用java实现而对javamail摸索了一段时间，总算有点收获。看到论坛中的经常有此方面的问题，因此把我的一些经验帖出来，希望对大家有些帮助。 此篇仅介绍用
  • 探索实体类存在的真正意义 java小叶檀 POJO
    一. 实体类简述    实体类其实就是俗称的POJO,这种类一般不实现特殊框架下的接口，在程序中仅作为数据容器用来持久化存储数据用的 POJO（Plain Old Java Objects）简单的Java对象   它的一般格式就是 public class A{ private String id; public Str
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他