Tensors
#Tensors
#Tensors和numpy中的ndarrays较为相似,因此Tensor也能够使用GPU来加速运算。
from__future__importprint_function
importtorch
x = torch.Tensor(5,3)#构造一个未初始化的5*3的矩阵
x = torch.rand(5,3)#构造一个随机初始化的矩阵
x#此处在notebook中输出x的值来查看具体的x内容
x.size()
#NOTE: torch.Size事实上是一个tuple,所以其支持相关的操作*
y = torch.rand(5,3)
#此处 将两个同形矩阵相加有两种语法结构
x + y#语法一
torch.add(x,y)#语法二
#另外输出tensor也有两种写法
result = torch.Tensor(5,3)#语法一
torch.add(x,y,out=result)#语法二
y.add_(x)#将y与x相加
#特别注明:任何可以改变tensor内容的操作都会在方法名后加一个下划线'_'
#例如:x.copy_(y), x.t_(),这俩都会改变x的值。
#另外python中的切片操作也是资次的。
x[:,1]#这一操作会输出x矩阵的第二列的所有值
Numpy桥
Numpy桥
将Torch的Tensor和numpy的array相互转换简直就是洒洒水啦。注意Torch的Tensor和numpy的array会共享他们的存储空间,修改一个会导致另外的一个也被修改。
# 此处演示tensor和numpy数据结构的相互转换
a = torch.ones(5)
b = a.numpy()
# 此处演示当修改numpy数组之后,与之相关联的tensor也会相应的被修改
a.add_(1)
print(a)
print(b)
# 将numpy的Array转换为torch的Tensor
import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
print(a)
print(b)
# 另外除了CharTensor之外,所有的tensor都可以在CPU运算和GPU预算之间相互转换
# 使用CUDA函数来将Tensor移动到GPU上
# 当CUDA可用时会进行GPU的运算
if torch.cuda.is_available():
x = x.cuda()
y = y.cuda()
x + y
Autograd: 自动求导
autograd 包提供Tensor所有操作的自动求导方法。
这是一个运行时定义的框架,这意味着你的反向传播是根据你代码运行的方式来定义的,因此每一轮迭代都可以各不相同。
以这些例子来讲,让我们用更简单的术语来看看这些特性。
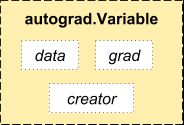
autograd.Variable 这是这个包中最核心的类。 它包装了一个Tensor,并且几乎支持所有的定义在其上的操作。一旦完成了你的运算,你可以调用 .backward()来自动计算出所有的梯度。
你可以通过属性 .data 来访问原始的tensor,而关于这一Variable的梯度则集中于 .grad 属性中。
还有一个在自动求导中非常重要的类 Function。
Variable
和 Function 二者相互联系并且构建了一个描述整个运算过程的无环图。每个Variable拥有一个 .creator
属性,其引用了一个创建Variable的 Function。(除了用户创建的Variable其 creator 部分是 None)。
如果你想要进行求导计算,你可以在Variable上调用.backward()。
如果Variable是一个标量(例如它包含一个单元素数据),你无需对backward()指定任何参数,然而如果它有更多的元素,你需要指定一个和tensor的形状想匹配的grad_output参数。
from torch.autograd import Variable
x = Variable(torch.ones(2, 2), requires_grad = True)
y = x + 2
y.creator
# y 是作为一个操作的结果创建的因此y有一个creator
z = y * y * 3
out = z.mean()
# 现在我们来使用反向传播
out.backward()
# out.backward()和操作out.backward(torch.Tensor([1.0]))是等价的
# 在此处输出 d(out)/dx
x.grad
神经网络
使用 torch.nn 包可以进行神经网络的构建。
现在你对autograd有了初步的了解,而nn建立在autograd的基础上来进行模型的定义和微分。
nn.Module中包含着神经网络的层,同时forward(input)方法能够将output进行返回。
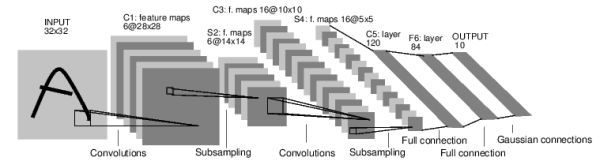
举个例子,来看一下这个数字图像分类的神经网络。
这是一个简单的前馈神经网络。 从前面获取到输入的结果,从一层传递到另一层,最后输出最后结果。
一个典型的神经网络的训练过程是这样的:
定义一个有着可学习的参数(或者权重)的神经网络
对着一个输入的数据集进行迭代:
用神经网络对输入进行处理
计算代价值 (对输出值的修正到底有多少)
将梯度传播回神经网络的参数中
更新网络中的权重
通常使用简单的更新规则: weight = weight + learning_rate*gradient
让我们来定义一个神经网络:
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 6, 5) # 1 input image channel, 6 output channels, 5x5 square convolution kernel
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16*5*5, 120) # an affine operation: y = Wx + b
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2)) # Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv2(x)), 2) # If the size is a square you can only specify a single number
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:] # all dimensions except the batch dimension
num_features = 1
for s in size:
num_features *= s
return num_features
net = Net()
net
'''神经网络的输出结果是这样的
Net (
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear (400 -> 120)
(fc2): Linear (120 -> 84)
(fc3): Linear (84 -> 10)
)
'''
仅仅需要定义一个forward函数就可以了,backward会自动地生成。
你可以在forward函数中使用所有的Tensor中的操作。
模型中可学习的参数会由net.parameters()返回。
params = list(net.parameters())
print(len(params))
print(params[0].size()) # conv1's .weight
input = Variable(torch.randn(1, 1, 32, 32))
out = net(input)
'''out 的输出结果如下
Variable containing:
-0.0158 -0.0682 -0.1239 -0.0136 -0.0645 0.0107 -0.0230 -0.0085 0.1172 -0.0393
[torch.FloatTensor of size 1x10]
'''
net.zero_grad() # 对所有的参数的梯度缓冲区进行归零
out.backward(torch.randn(1, 10)) # 使用随机的梯度进行反向传播
注意: torch.nn 只接受小批量的数据
整个torch.nn包只接受那种小批量样本的数据,而非单个样本。 例如,nn.Conv2d能够结构一个四维的TensornSamples x nChannels x Height x Width。
如果你拿的是单个样本,使用input.unsqueeze(0)来加一个假维度就可以了。
复习一下前面我们学到的:
1. torch.Tensor - 一个多维数组
2. autograd.Variable - 改变Tensor并且记录下来操作的历史记录。和Tensor拥有相同的API,以及backward()的一些API。同时包含着和张量相关的梯度。
3. nn.Module - 神经网络模块。便捷的数据封装,能够将运算移往GPU,还包括一些输入输出的东西。
4. nn.Parameter - 一种变量,当将任何值赋予Module时自动注册为一个参数。
5. autograd.Function - 实现了使用自动求导方法的前馈和后馈的定义。每个Variable的操作都会生成至少一个独立的Function节点,与生成了Variable的函数相连之后记录下操作历史。
到现在我们已经明白的部分:
1.定义了一个神经网络。
2.处理了输入以及实现了反馈。
仍然没整的:
1.计算代价。
2.更新网络中的权重。
一个代价函数接受(输出,目标)对儿的输入,并计算估计出输出与目标之间的差距。
代价函数
一个简单的代价函数:nn.MSELoss计算输入和目标之间的均方误差。
举个例子:
output = net(input)
target = Variable(torch.range(1, 10)) # a dummy target, for example
criterion = nn.MSELoss()
loss = criterion(output, target)
'''loss的值如下
Variable containing:
38.5849
[torch.FloatTensor of size 1]
'''
现在,如果你跟随loss从后往前看,使用.creator属性你可以看到这样的一个计算流程图:
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d -> view -> linear -> relu -> linear -> relu -> linear -> MSELoss -> loss
因此当我们调用loss.backward()时整个图通过代价来进行区分,图中所有的变量都会以.grad来累积梯度。
# For illustration, let us follow a few steps backward
print(loss.creator)#MSELoss
print(loss.creator.previous_functions[0][0])#Linear
print(loss.creator.previous_functions[0][0].previous_functions[0][0])# ReLU
# 现在我们应当调用loss.backward(), 之后来看看 conv1's在进行反馈之后的偏置梯度如何
net.zero_grad() # 归零操作
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
''' 这些步骤的输出结果如下
conv1.bias.grad before backward
Variable containing:
0
0
0
0
0
0
[torch.FloatTensor of size 6]
conv1.bias.grad after backward
Variable containing:
0.0346
-0.0141
0.0544
-0.1224
-0.1677
0.0908
[torch.FloatTensor of size 6]
'''
现在我们已经了解如何使用代价函数了。
阅读材料:
神经网络包中包含着诸多用于神经网络的模块和代价函数,带有文档的完整清单在这里:torch.nn - PyTorch 0.1.9 documentation
更新网络的权重
最简单的更新的规则是随机梯度下降法(SGD):
weight = weight - learning_rate * gradient
我们可以用简单的python来表示:
learning_rate = 0.01
for f in net.parameters():
f.data.sub_(f.grad.data * learning_rate)
然而在你使用神经网络的时候你想要使用不同种类的方法诸如:SGD, Nesterov-SGD, Adam, RMSProp, etc.
我们构建了一个小的包torch.optim来实现这个功能,其中包含着所有的这些方法。 用起来也非常简单:
import torch.optim as optim
# create your optimizer
optimizer = optim.SGD(net.parameters(), lr = 0.01)
# in your training loop:
optimizer.zero_grad() # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step() # Does the update