理论力学辅助:
Lf[tt_, vv_, var__, t_] :=
Module[{l = Simplify[tt - vv], n = Length[var], i = 0},
Table[D[D[l, D[var[[i]], t]], t] - D[l, var[[i]]], {i, 1, n}]
]
例子:
In[1]:= Lf[1/2 m x1'[t]^2 + 1/2 m x2'[t]^2,
1/2 k (x1[t]^2 + x2[t]^2), {x1[t], x2[t]}, t]
Out[1]= {k x1[t] + m (x1^\[Prime]\[Prime])[t],
k x2[t] + m (x2^\[Prime]\[Prime])[t]}
大物实验助手:
处理数据:
FixData[list_List, f_Function] :=
Module[{l = Length[list]}, Table[f[list[[i]]], {i, 1, l}]]
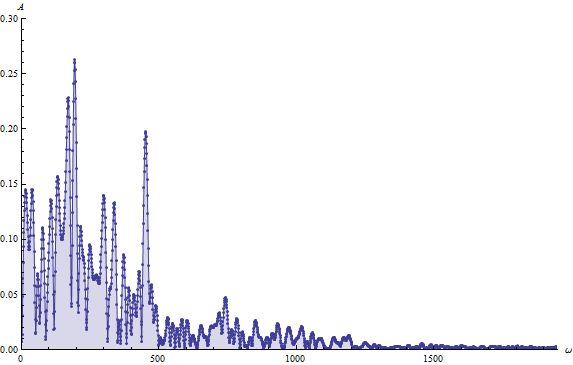
离散函数频谱分析:
注:正在完善之中
FuL[l_List, \[Omega]_, \[Delta]t_, {a_, b_}] :=
1/Abs[b - a] Total@
Table[l[[i]] \[Delta]t E^(I \[Omega] i \[Delta]t), {i, 1,
Length[l]}]
(*使用示例*)
ls = Table[Evaluate[x[t] /. s], {t, 0, 200, 0.1}];(*s是一个混沌方程的解*)
PL = Flatten@
Table[FuL[ls, \[Omega], 0.1, {0, 200}], {\[Omega], 0.1, 4, 0.002}];
| 函数名称 | 用途 | 格式 |
|---|---|---|
FuL |
计算频谱,输出列表 | FuL[离散列表, 角频率, 间隔时间, {起始, 结束}] |
复变函数绘图好帮手:
TransComplexPlot[w_, f_, {x_, xf_, xz_}, {y_, yf_, yz_},
PlotPoints -> n_, PlotRange -> {{l_, r_}, {d_, u_}}] :=
ParametricPlot[{Re[w[f]], Im[w[f]]}, {x, xf, xz}, {y, yf, yz},
PlotPoints -> n, PlotRange -> {{l, r}, {d, u}}]
使用示例:
| 可使用选项 | 用途 | 格式 |
|---|---|---|
PlotPoints |
控制细致程度 | PlotPoints->n |
PlotRange |
绘图范围 | PlotRange -> {{l, r}, {d, u}} |
波动光学绘图
Len = Compile[{{x, _Real}, {y, _Real}, {z, _Real}, {x2, _Real}, {y2, \
_Real}, {z2, _Real}},
If[{x, y, z} != {x2, y2, z2}, Sqrt[
N[(x - x2)^2 + (y - y2)^2 + (z - z2)^2]], 1.0]]
PutDot = Compile[{{x, _Real}, {y, _Real}, {z, _Real}, {\[CurlyPhi], \
_Real}, {\[Omega], _Real}, {W, _Real}, {b, _Real}, {L, _Integer}},
Table[N[
W/(b*Len[x, y, z, i, j, 0])*
E^(-I (\[Omega] b*Len[x, y, z, i, j, 0] + \[CurlyPhi]))], {i, 1,
L}, {j, 1, L}]
]
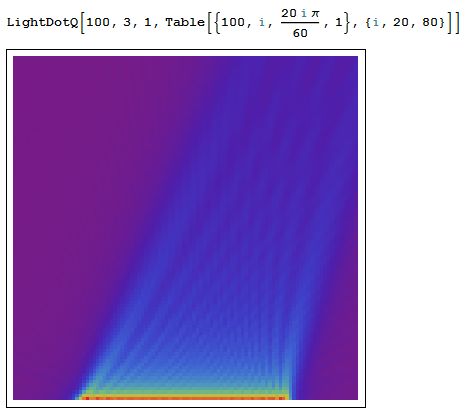
LightDotQ[n_, \[Omega]_, b_, DList_] := Module[
{x = Length[DList], LightPx = Table[0, {i, 1, n}, {j, 1, n}]},
LightPx =
Abs[Sum[PutDot[DList[[k]][[1]], DList[[k]][[2]], 0,
DList[[k]][[3]], \[Omega], DList[[k]][[4]], b, n], {k, 1, x}]];
ArrayPlot[LightPx, ColorFunction -> "Rainbow"]
]
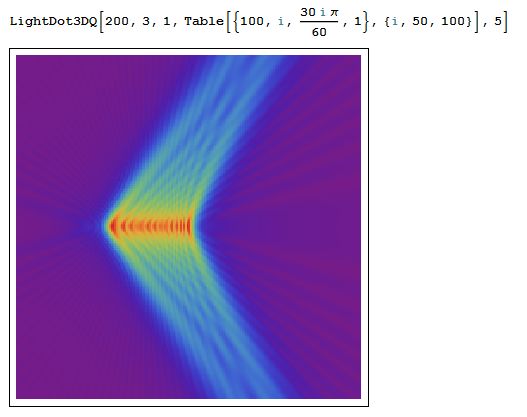
LightDot3DQ[n_, \[Omega]_, b_, DList_, z_] :=
Module[
{x = Length[DList], LightPx = Table[0, {i, 1, n}, {j, 1, n}]},
LightPx =
Abs[Sum[PutDot[DList[[k]][[1]], DList[[k]][[2]], z,
DList[[k]][[3]], \[Omega], DList[[k]][[4]], b, n], {k, 1, x}]];
ArrayPlot[LightPx, ColorFunction -> "Rainbow"]
]
使用示例:
使用说明:
| 函数/变量名称 | 用途 | 格式 |
|---|---|---|
LightDotQ |
绘制二维空间的光场 | LightDotQ[图像大小, 光的频率, 空间密度, 光点序列] |
LightDot3DQ |
绘制三维空间的光场投到二维平面上的光强分布 | LightDot3DQ[图像大小, 光的频率, 空间密度, 光点序列, 光点高度] |
| 光点序列 | 描述一个光点 | {x,y,初相位,光强} |
遗传算法程序包(不完整)
1.建立种群:
MakeGroup[Num_Integer, f_Function] := Table[f[i], {i, 1, Num}]
示例:
In[1] = MakeGroup[10, Sin[#/2] &]
Out[1] = {Sin[1/2], Sin[1], Sin[3/2], Sin[2], Sin[5/2], Sin[3], Sin[7/2],
Sin[4], Sin[9/2], Sin[5]}
| 函数名称 | 用途 | 格式 |
|---|---|---|
MakeGroup |
建立种群 | MakeGroup[种群规模, 生成函数] |
2.基因交换
基础模式:
Swap[List1_List, List2_List, {S_Integer, T_Integer}] :=
(*基因一,基因二,{开始交换点,终止交换点}*)
Block[
{Len = Length[List1], Len2 = Length[List2]},
If[Len != Len2, Null,(*若长度不等,返回Null*)
(*Table[If[S\[LessEqual]i\[LessEqual]T,
List2\[LeftDoubleBracket]i\[RightDoubleBracket],
List1\[LeftDoubleBracket]i\[RightDoubleBracket]],{i,1,Len}]交换*)
List1[[1 ;; S - 1]]~Join~List2[[S ;; T]]~Join~List1[[T + 1 ;; Len]]
]
]
| 函数名称 | 用途 | 格式 |
|---|---|---|
Swap |
基因交换 | Swap[基因1, 基因2, {起始点, 终止点}] |
基因突变:
Changex[GeList_List, Pc_Integer, {f_Function, Kind_String}] := Block[
{GeCopy = GeList},
Switch[(*考虑多种变化选项*)
Kind,
"Change", GeCopy[[Pc]] = f[GeCopy[[Pc]]],
"Add", GeCopy[[Pc]] += f[GeCopy[[Pc]]]]; GeCopy
]
GeChange[p_Real, GeList_List, n_Integer, {f_Function, Kind_String}] :=
(*突变概率,基因序列,突变n次,{突变函数,突变模式}*)
Block[
{Len = Length[GeList],
Pc = 0,
GeCopy = 0
},
If[RandomReal[] < p,
GeCopy = GeList;
Nest[Changex[#, RandomInteger[{1, Len}], {f, Kind}] &, GeCopy, n](*n次迭代*)
, GeList]
]
GeChangeList[GeList_List, pList_List, {f_Function, Kind_String}] :=
(*基因序列,突变序列,{突变函数,突变模式}*)
Block[
{Len = Length[GeList],
Pc = 0,
GeCopy = GeList
},
Do[GeCopy = Changex[GeCopy, pList[[i]], {f, Kind}];, {i, 1, Length[pList]}];
GeCopy
]
GePMC[GeList_List, {S_Integer, T_Integer}] :=(*部分重排序*)
(*需要突变的基因,{开始位,结束位}*)
Module[{GeCopy = GeList,
head = GeList[[1 ;; S - 1]],
body = GeList[[S ;; T]],
foot = GeList[[T + 1 ;; Length[GeList]]]
},
head~Join~Reverse[body]~Join~foot
]
示例:
随机变异一个基因:
基因倒位:
| 函数名称 | 用途 | 格式 |
|---|---|---|
GeChange |
基因随机变异 | GeChange[突变概率,基因序列,突变n次,{突变函数,突变模式}] |
GePMC |
基因倒位 | GePMC[需要突变的基因,{开始位,结束位}] |
第二次更新于2014年11月20日