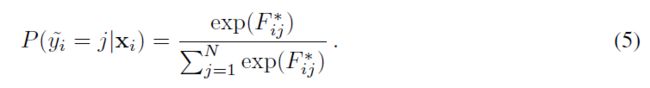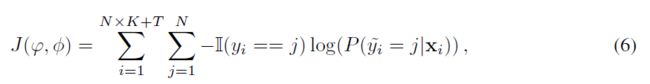1. 论文相关
CVPR2018
学习传播标签:用于小样本学习的传导传播网络
2.摘要
2.1 摘要
小样本学习的目标是学习一个分类器,即使在每个类的训练实例数量有限的情况下,该分类器也能很好地泛化。最近引入的元学习方法通过在大量的多类分类任务中学习一个通用分类器并将模型推广到一个新任务中来解决这个问题。然而,即使有了这样的元学习,新分类任务中的小数据问题(low-data problem)仍然存在。本文提出了一种新的元学习框架:传导传播网络(Transductive Propagation Network ,TPN),它可以同时对整个测试集进行分类,以缓解小数据量的问题。具体来说,我们建议通过学习利用数据中的流形结构的图构造模块,学习如何将标签从标记实例传播到未标记的测试实例。TPN以端到端的方式联合学习特征嵌入参数和图构造参数。我们验证了TPN在多个基准数据集上,它在很大程度上优于现有的小样本学习方法,并取得了最先进的结果。
2.2 思想
在有限的训练数据量下实现更大改进的一种方法是考虑测试集中实例之间的关系,从而将它们作为一个整体进行预测,这被称为传导或传导推理。在以往的工作中(Joachims,1999;Zhou等人,2004;Vapnik,1999),传导推理已经显示出优于归纳方法,归纳方法可以逐个预测测试实例,特别是在小训练集中。一种流行的转导方法是在标记和未标记的数据上构建一个网络,并在它们之间传播标记以进行联合预测。然而,这种标签传播(和转导)的主要挑战是,标签传播网络通常是在不考虑主要任务的情况下获得的,因为不可能在测试时学习它们。
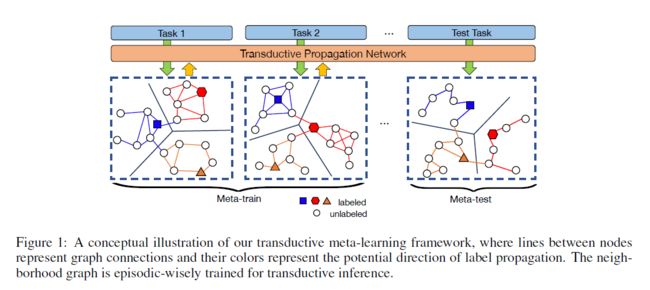
然而,使用基于episodic training的元学习,我们可以学习标签传播网络(label propagation network),因为从训练集中抽取的查询示例可以用来模拟真实的测试集进行传导推理。基于这一发现,我们提出了一种传输网络(TPN)来解决低数据问题。我们不使用归纳推理,而是使用整个查询集进行transductive推理(参见图1)。具体来说,我们首先使用一个深度神经网络将输入映射到一个嵌入空间。在此基础上,利用支持集和查询集的结合,提出了一个图构造模块来开发新类空间的流形结构。根据图的结构,采用迭代的标签传播方法将标签从支持集传播到查询集,最终得到一个封闭的解决方案(closed-form solution)。利用查询集的传播分数和基真值标签,计算了特征嵌入和图构造参数的交叉熵损失。最后,所有参数都可以使用反向传播进行端到端更新。
2.3主要贡献
这项工作的主要贡献有三方面。
(1)据我们所知,我们是第一个在小样本学习中明确地建立传导推理模型的人。尽管Nichol等人(2018)在传导设置下进行实验,他们只通过批量规范化在测试示例之间共享信息,而不是直接提出传导模型。
(2)在间接推理(transductive inference)中,我们提出通过episodic meta-learning,学习在不可见类的数据实例之间传播标签。这个学习的标签传播图是显示出显著优于基于朴素启发式的标签传播方法(naive heuristic-based label propagation methods)。
(3)我们在两个基准数据集上评估了我们的方法,即minimagenet和tieredImageNet。实验结果表明,我们的传导传播网络(Transductive Propagation Network)在两个数据集上都优于最新的方法。同时,通过半监督学习,我们的算法取得了更高的性能,优于所有的半监督小样本学习基线。
我们的算法假设了一个transductive设置,在这个设置中,我们利用支持集和查询集的结合来利用新类空间的流形结构。
3. 主要方法(MAIN APPROACH)
在本节中,我们将介绍利用小样本分类任务的流形结构所提出的算法来提高性能。
3.1 问题定义(PROBLEM DEFINITION)
3.2 传导传播网络 (TRANSDUCTIVE PROPAGATION NETWORK ,TPN)
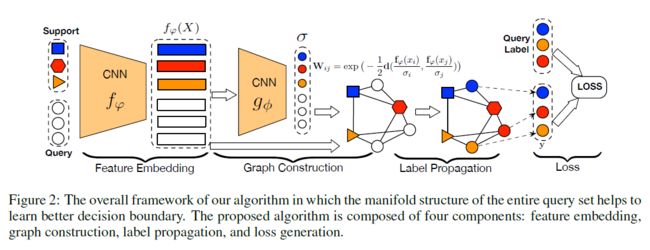
我们介绍了图2中所示的传导传播网络(TPN),它包括四个部分:用卷积神经网络嵌入特征;构造生成示例参数以利用流形结构;从支持集S到查询集Q传播标签;计算在Q上传播的标签和真值之间的交叉熵损失,以联合训练框架。
3.2.1特征嵌入
我们采用卷积神经网络来提取输入的特征,其中指的是特征图,表示网络的参数。尽管有普遍性,我们还是采用最近几个工作中使用的同一架构(Snell等人,2017;Sung等人,2018;Vinyals等人2016年)。通过这样做,我们可以在实验中提供更公平的比较,突出显示传导途径(transductive approach)的影响。网络由四个卷积块组成,其中每个块以一个33核的二维卷积层开始,滤波器大小为64。每个卷积层之后是批量规范化层(Ioffe和Szegedy,2015),一个ReLU非线性和22最大池层。对于支持集S和查询集Q,我们使用相同的嵌入函数。
3.2.2 图构造(GRAPH CONSTRUCTION)
流形学习(Chung and Graham,1997;Zhou et al.,2004;Yang et al.,2016)发现数据中嵌入的低维子空间,选择合适的邻域图是关键。常见的选择是高斯相似函数(Gaussian similarity function):
其中是距离度量(例如欧几里德距离),是长度标度参数(length scale parameter)。邻域结构(neighborhood structure)在不同表现出不同的行为,这意味着它需要仔细选择最佳的以达到最好的标签传播性能(Wang and Zhang,2006;Zhu and Ghahramani,2002)。此外,我们观察到在元学习框架中没有调整尺度参数的原则性方法,尽管存在一些降维方法的启发(Zelnik-Manor and Perona,2004;Sugiyama,2007)。
Example-wise length-scale parameter
在元学习中,为了得到一个合适的邻域图,提出了一种基于支持集和查询集的联合集S∪Q的图构造模块。该模块由卷积神经网络组成,该卷积神经网络对于采用特征映射产生一个示例性的长度尺度参数。需要注意的是,该scale parameter是通过example-wisely确定的,并且是在episodic training procedure中学习的,它很好地适应不同的任务,并且适合于小样本学习。图构造模块由两个卷积块(64和1个滤波器)和两个全连接层(8和1个神经元)组成,如附录A。我们的相似性函数定义如下:
式中,对于S∪Q中的所有实例。我们只保留W的每一行的K个最大值来构造一个K近邻图(k-nearest neighbour graph)。然后我们在W上应用正规化图Laplacians(the normalized graph Laplacians),即,,其中D是一个对角矩阵,其(i,i)值是W第i行的和。
Graph construction structure
图构造模块的结构如图3所示。它由两个卷积块和两个完全连接的层组成,其中每个块包含一个3×3卷积、批处理规范化、ReLU激活,然后是2×2最大池化。每个卷积块中的滤波器数目分别为64和1。为了提供一个示例级的缩放参数(example-wise scaling parameter),将来自第二卷积块的激活图通过两个全连接层(其中神经元的数目分别为8和1)转换为标量。
Graph construction in each episode
在每一episodic的图构建中,我们遵循小样本元学习器训练的episodic范式(episodic paradigm)。这意味着图是为每个episodic中的每个任务单独构建的,如图1所示。一般情况下,在5-way 5-shot的训练中,N=5,K=5,T=75,W尺寸只有100×100,效率相当高。
3.2.3 标签传播(LABEL PROPAGATION)
我们现在描述如何在最后一个交叉熵损失步骤之前,使用标签传播获得查询集Q的预测。设F表示具有非负项的(N×K+T)×N矩阵的集合。我们定义了一个标签矩阵Y∈F,如果它来自于支持集,并且标签为则,否则为。从Y开始,标签传播使用以下公式根据图结构迭代确定联合集中S∪Q中样本的未知标签:
式中,表示时间戳t处的预测标签,S表示归一化权重,α∈(0,1)控制传播信息的量。众所周知,序列具有如下的闭式解:
其中I是单位矩阵(identity matrix)(Zhou等人,2004)。我们直接利用这一结果进行标签传播,使得整个episodic meta-learning过程在实践中更加有效。
时间复杂度(Time complexity)
矩阵求逆(Matrix inversion)最初采用时间复杂度,这对于较大的n来说是低效的。但是,在我们的设置中,n=N×K+T(80表示1-shot,100表示5-shot)非常小。此外,在标签传播的可扩展性和效率方面已有大量的工作,如Liang和Li(2018);Fujiwara和Irie(2014),这可以将我们的工作扩展到大规模数据。在附录A.4中提出了更多的讨论。
3.2.4 分类损失产生(CLASSIFICATION LOSS GENERATION)
这一步的目的是计算通过标签传播的支持集和查询集的联合预测与真值之间的分类损失。我们从S∪Q计算预测分数和真值标签之间的交叉熵损失,以端到端的方式学习所有参数,其中使用softmax转换为概率分数:
这里,表示支持和查询集并集中的第i个实例的预测标签,表示标签传播预测标签的第j个分量。然后损失函数计算如下:
式中,表示的真值标签,是指示函数(indicator function),如果b为真Ⅱ(b)=1,否则为0。
注意,在等式(6)中,损失取决于两组参数ϕ和φ(即使依赖关系是隐式的)。所有这些参数都是由episodic training以端到端的方式联合更新的。
4. 实验
我们在两个数据集,即miniImageNet(Ravi and Larochelle,2017)和tieredImageNet(Ren et al.,2018)上评估和比较我们的TPN和最新方法。前者是最受欢迎的小样本学习基准,后者是最近发布的一个更大的小样本学习数据集。
4.1 数据集
miniImageNet
miniImageNet数据集是Imagenet(Krizhevsky等人,2012)的集合,用于少量镜头图像识别。它由100个从Imagenet中随机选择的类组成,每个类包含600个示例。为了直接与最先进的算法进行比较
很少有射击学习,我们依赖Ravi和Larochelle(2017)使用的分班法,包括64个训练班、16个验证班和20个测试班。所有图像的大小都调整为84×84像素。
tieredImageNet
与miniImageNet类似,tieredImageNet(Ren et al.,2018)也是Imagenet的一个子集(Krizhevsky et al.,2012),但它有更多来自ILSVRC-12的类(miniImageNet有608个类,而不是100个类)。与minimagenet不同,它具有与Imagenet中的高级节点相对应的更广泛类别的层次结构。最高层共有34个类别,分为20个训练类别(351个类别)、6个验证类别(97个类别)和8个测试类别(160个类别)。每个类中的平均示例数是1281。这种高级的分割策略确保训练类在语义上与测试类不同。这是一个更具挑战性和现实性的少镜头设置,因为没有假设训练班应该类似于测试班。同样,所有图像的大小都调整为84×84像素。
4.2 实验设置
为了与其他方法进行公平比较,我们采用广泛使用的CNN(Finn等人,2017;Snell等人,2017)作为特征嵌入函数(第3.2.1节)。k近邻图的超参数k(第3.2.2节)设置为20,标签传播的超参数α设置为0.99,如Zhou等人所建议的(2004年)。
如Snell等人一样,我们采用episodic training procedure,即,我们抽样一组N-way K-shot训练任务来模拟N-way K-shot测试问题。此外,Snell等人。(2017)提出了“HigherWay”的训练策略,在每episodic中使用的训练样本多于测试样本。然而,我们发现,与测试阶段相比,使用更多的示例进行训练是有益的(附录A.1)。这在我们的实验中被称为“Higher Shot”。对于1-shot 和 5-shot测试问题,我们分别采用5-shot 和 10-shot训练。在所有设置中,查询数量设置为15,从测试集随机生成600个episodic然后平均性能。
我们所有的模型都接受了Adam(Kingma和Ba,2015)的训练,初始学习率为。对于miniImageNet,我们每10000 episode将学习率降低一半;对于tieredImageNet,我们每25000 episode将学习率降低一半。衰减步骤变大的原因是tieredimagnet在每个类中有更多的类和更多的示例,这需要更大的训练迭代。我们运行了训练过程,直到验证损失达到一个平稳状态。
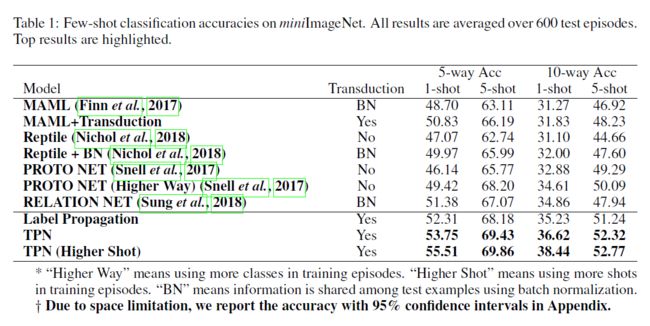
4.3 小样本学习结果(FEW-SHOT LEARNING RESULTS)
我们将我们的方法与不同设置下的几种最新方法进行比较。尽管transductive方法从未被显式地使用过,但批处理规范化层被transductive地用于在测试示例之间共享信息。例如,在Finn等人。(2017);Nichol等人。(2018年),他们使用查询批统计信息(query batch statistics)而不是全局BN参数(global BN parameters)进行预测,这将导致查询集中的性能提高。此外,我们还提出了两种简单的传导方法(transductive methods),作为显式利用查询集的基线。首先,我们提出了MAML+传导机制(MAML+Transduction),损失函数轻微修改为:
附加项用作传导正则化。第二,提出了一种基于朴素启发式的标签传播方法(naive heuristic-based label propagation methods,Zhou等人,2004),用于显式地建模传导推理。
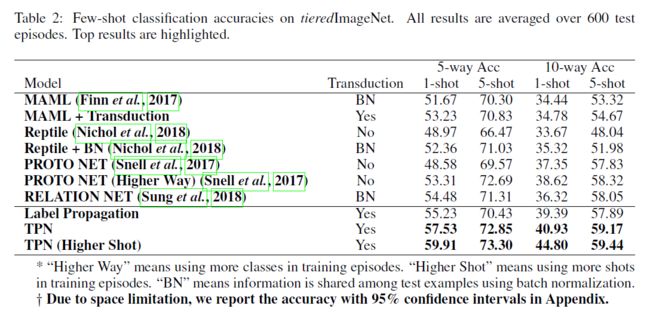
实验结果见表1和表2。除了“HigherWay”的原型网络外,传递批量规范化(Transductive batch normalization)方法往往比纯归纳方法执行得更好。在大多数情况下,不学习传播的标签传播优于其他基线方法,这证明了转导(transduction)的必要性。所提出的TPN算法在regular shots下训练时,取得了最先进的效果,并且在很大程度上优于其他算法。当采用“Higher Shot”时,TPN的性能继续提高,尤其是在1-shot情况下。这证实了我们的模型通过学习构造用于标签传播的图,有效地发现了测试示例的episodic式流形结构(episodic-wise manifold structure)。
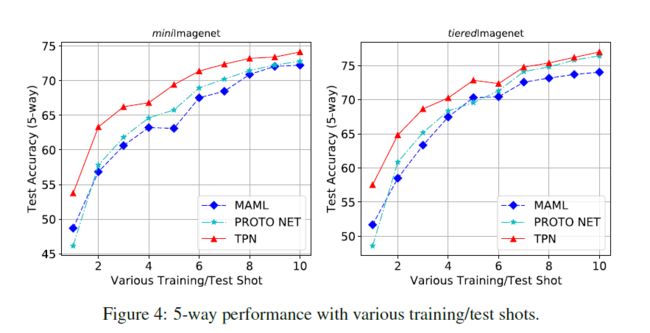
另一个观察结果是,5-shot分类的优点不如1-shot分类的显著。例如,在5-way minimagenet中,TPN相对于已发布的最新技术的绝对改善率为4.13%(对于1-shot)和1.66%(对于5-shot)。为了进一步研究这一点,我们进行了5-way k-shot (k = 1; 2; ... ; 10)实验。结果如图4所示。我们的TPN在不同shot下的性能始终优于其他方法。而且,可以看出TPN的性能优于其他方法,在较低的shot下有较大的margin。随着shot的增加,由于使用了更多的标记数据,转导(transduction)的优势逐渐缩小。这一发现与TSVM(Joachims,1999)中的结果一致:当有更多的训练数据可用时,transductive inference的贡献将减少。
4.4 与半监督小样本学习的比较
传统的半监督学习和传导的主要区别在于未标记数据的来源。传导式方法直接使用测试集作为未标记数据,而半监督学习通常有一个额外的未标记集。为了与半监督方法进行比较,我们提出了一个半监督的TPN版本,称为TPN-semi,它通过从标记集和额外的未标记集传播标签,每次对一个测试示例进行分类。
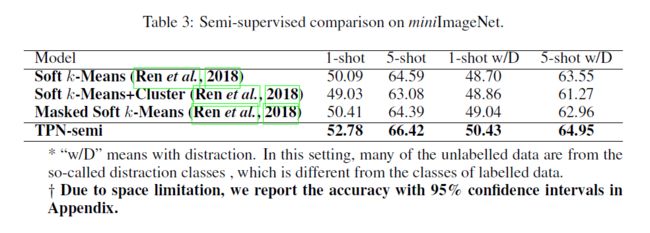
我们使用minimagenet和tieredImageNet对Ren等人提出的有标签/无标签数据进行分割。(2018年)。具体来说,他们将每个类的图像分割成不相交的标记集和未标记集。对于minimagenet,每个类中标记/未标记数据的比率分别为40%和60%。同样,tieredImageNet的比率是10%和90%。所有半监督方法(包括TPN半监督方法)从标记集(例如,40%来自miniImageNet)和从未标记集(例如,60%来自miniImageNet)提取未标记数据的样本支持/查询数据。此外,还有一种更具挑战性的情况,即许多来自其他干扰类(不同于标记类)的未标记示例。
以下为Ren等人。(2018年),我们报告了超过10个随机标记/未标记拆分的平均精度以及在标准误差中计算的不确定度。结果见表3和表4。可以看出,TPN算法在性能上比其他算法有较大的优势,尤其是在单次情况下。尽管TPN最初是设计用来进行传导式推理的,但我们证明它可以成功地适应半监督学习任务,而且几乎不需要修改。在某些无法得到全部测试数据的情况下,TPN-semi算法可以作为一种有效的替代算法。
5. 结论
在这项工作中,我们提出了一种用于小样本学习的导入式设置(transductive setting)。我们提出的方法,即传导性传播网络(Transductive Propagation Network,TPN),利用整个测试集进行传导性推理。具体来说,我们的方法由四个步骤组成:特征嵌入、图构造、标签传播和损失计算。图的构造是一个关键步骤,它可以生成示例参数(examplewise parameters)来利用每一episode中的流形结构。在我们的方法中,所有的参数都是使用交叉熵损失,相对于查询集中的真值标签和预测分数进行端到端的学习。我们在minimagenet和tieredImageNet上获得了最先进的结果。此外,与其他半监督方法相比,该算法的半监督自适应效果更高。在以后的工作中,我们将探索episodic-wise距离度量,而不是仅使用欧氏距离的示例参数(example-wise parameters)。
参考资料
[1] ICLR2019少样本学习新思路:利用转导(Transductive)和标签传播
[2] 论文:learning to propagate labels :transductive propagation network for few-shot learning
[3]
论文下载
[1] Transductive Propagation Network for Few-shot Learning
代码
[1] # csyanbin/TPN