coci 2012 inspektor
街道由左到右分布着\(N\)个办公室,编号为\(1\)到\(N\),最开始,每个办公室都是空的,一些公司将入住,并赶走办公室里面现有的公司。一人每天会路过一些连续的办公室。他会查帐,找到最富的公司。
公司入住的描述如下:
\(1\ T\ K\ Z\ S\),\(T\)表示搬来的时间,\(K\)表示入住的办公室编号,\(Z\)表示公司每天的收益,\(S\)表示原来的余额。如果办公室原来有单位,原来的将离开,公司入住当天没有收益。
对于查帐的描述:
\(2\ T\ A\ B\) , \(T\)表示查帐的时间。\(A\)和\(B\)表示要查的办公室在\(A\)和\(B\)之间(包涵端点)。查帐时要算当天的收益。
输入
第一行两个正整数 \(N (1 ≤ N ≤ 100 000) and M (1 ≤ M ≤ 300 000)\),表示办公室的间数,\(M\)表示有\(M\)个事件。
接下来\(M\)行,每行描述一个事件\(1\ T\ K\ Z\ S\) 或\(2\ T\ A\ B\)所有事件按时间顺序给出。 每天最多发生一个事件,所以\(T\)严格递增 \(T\)小于\(10^6\),$ Z\(和\)S $的绝对值小于\(10^6\).
输出
对于每一次查帐输出一行,表示最富的公司的钱数,如果没有公司输出\(nema\).
input
2 4
1 1 1 2 4
1 2 2 3 2
2 5 1 2
2 7 1 2output
12
17input
3 6
1 1 1 4 -2
1 2 2 2 6
2 3 3 1
2 4 3 1
1 5 3 -6 20
2 6 2 3output
8
10
14input
5 9
1 1 5 4 -5
2 2 3 5
1 3 4 6 9
2 4 1 2
1 6 2 2 3
2 8 2 1
1 9 4 0 17
2 10 5 5
2 11 1 4output
-1
nema
7
31
17当前是第\(T\)天时,对于每一个公司,盈利是
\[(T-T_0)*z_i+s_i\]
其中,\(T_0,z_i,s_i\)分别表示,搬来的时间,每天盈利,初始盈利;
等价于
\[T*z_i+s_i-T_0*z_i\]
发现这是一个一次函数,意味着每个公司都可以用一条直线来表示;
我们可以维护每个时间点的坐标系,找到当\(x\)取\(T\)时的最大值,这就是答案;
我们先不考虑修改操作;看怎样找到\(T\)取值下的最大值;
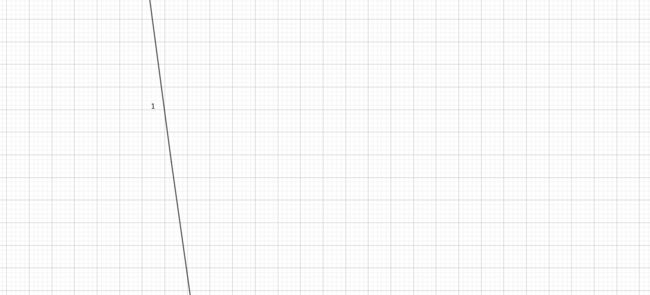
在一个坐标系里,有可能被取成最大值只可能是最上面的直线;
比如:
只有红色部分可能是答案直线,我们也只用维护这一部分;
这其实就是一个下凸壳,我们可以用单调栈来构造,用一个指针扫描来寻找答案;
关于下凸壳的构造
我们需要按顺序维护出在下凸壳上的直线的编号,
可以发现下凸壳上的直线的斜率是单调递增的,两两直线的交点与直线对应,横坐标也是单调递增的;
我们先把直线按斜率大小排序(小的在前
我们可以按横坐标维护一个存交点的单调栈;
因为交点也是两条直线得来的,我们可以直接把直线放到栈内,相邻两条直线的交点的横坐标保证单调递增;
当我们新加入一条直线时,如果这条直线与栈顶直线的交点,在栈顶交点(就是栈顶直线与栈内的第二条直线的交点,它的横坐标是当前最大的) 右边,那么这条直线可以直接加入栈中;
如果在栈顶交点的左边,应当把栈顶交点弹出(其实就是把栈顶直线弹出,这个交点就没有了),直到当前直线与栈顶直线的交点成为最大值,再把当前直线加入栈中。(单调栈的基本操作)
最后栈内的直线,就是下凸壳中的直线;
举个例子
我先加入第一条直线,这是斜率最小的一条直线
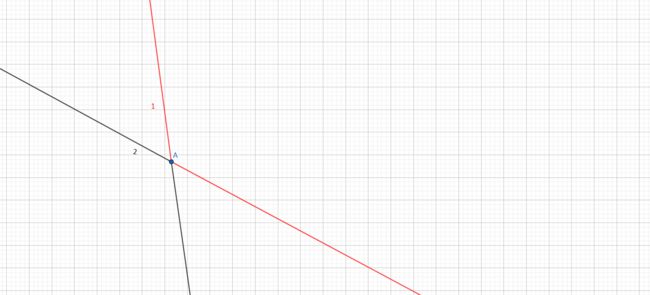
再加入第二条直线,因为当前栈内直线只有一条,还没有交点,就直接加入
红色部分就是当前栈维护出的下凸壳;
\(A\)就是现在横坐标最大的交点
再加入第三条直线,它与第二条直线的交点在\(A\)右边,我们可以直接加入;
\(B\)就是现在横坐标最大的交点
第三条直线是栈顶直线,红色部分是下凸壳
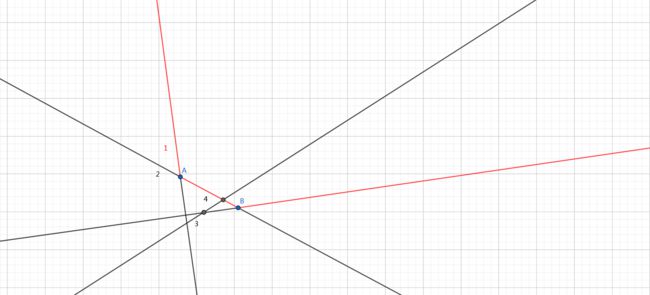
再加入第四条直线,它与第三条直线的交点在\(B\)左边,我们发现第三条直线已不能在下凸壳里了,应先把第三条直线弹出,
再发现第四条直线与第二条直线的交点在\(A\)右边,可以加入第四条直线;
现在的\(B\)是横坐标的最大的交点
栈内元素应该是\(1,2,4\),也就是下凸壳中的直线(红色部分);
构造的时间复杂度是\(O(nlogn)\)
关于在已有下凸壳上求解
我们想知道横坐标是\(T\)时,下凸壳上的纵坐标;
主要目的就是找\(x=T\)这条直线与哪条直线相交
根据之前的操作,我们知道下凸壳中直线的分界是依据交点的;
我们先要保证交点与直线对应,
假设这个交点所对应的直线是相交的两条直线的前一条;
我们找到第一个横坐标大于等于\(T\)的交点,那么它对应的直线应该与\(x=T\)相交,也就是答案直线;
当前第一个大于等于\(T\)的交点是\(B\),可知\(x=T\)与直线\(2\)相交
又由于我们询问的\(T\)是严格单增的,那答案交点也是单增的,我们只需要记录这个凸壳已经被扫到哪里了,下次从这里开始就可以了;
查询的总时间复杂度是\(O(T)\)
考虑有修改操作的情况
修改具有不可继承性,修改后的凸壳和之前的凸壳是可能没有相同点的;
修改一条直线可能改变凸壳的全貌;
意味着每次修改一条直线,都需要重构凸壳,这样成本太高了;
我们可以考虑分块;
对\(n\)分块,假设每个块大小是\(B\),我们在每个块中维护一个这个区间的凸壳;
对于查询,不是整块的暴力扫描,是整块的用指针在对应块找答案,前者复杂度是\(O(B)\),后者总时间复杂度是\(O(\frac{n}{B}*T)\),\(T\)是最大时间;
对于修改,把待修改的块打上标记,当调用它是进行一次重构,对于一次重构时间复杂度是\(O(BlogB)\)
\(Code\)
#include
#define ll long long
#define re register
using namespace std;
const int N=100005;
int n,m,len,opt;
int pos[N],L[N],R[N];
struct line
{
ll k,b;//斜率和截距
bool operator<(line l)const
{
return k==l.k?b>l.b:ky?x:y;}
inline int read()
{
int x=0,f=1;char st=getchar();
while(st<'0'||st>'9'){if(st=='-') f=-1;st=getchar();}
while(st>='0'&&st<='9') x=x*10+st-'0',st=getchar();
return x*f;
}
inline void write(ll x)
{
if(x<0) x=~x+1,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline double getx(line x,line y)
{
return (double)(x.b-y.b)/(y.k-x.k); //算两条直线交点的横坐标
}
inline void rebuild(int x)
{
int st=L[x]-1,top=L[x];
for(re int i=L[x];i<=R[x];++i)
if(vis[i]) b[++st]=a[i]; //把需要重构的直线加入
sort(b+L[x],b+st+1);
sta[top]=L[x];
for(re int i=L[x]+1;i<=st;++i)
if(b[i].k!=b[i-1].k) //如果两条直线斜率相同,只可能取到截距大的一条
{
while(top>L[x]&&getx(b[i],b[sta[top]])r) swap(l,r);
ll tmp=-1e18;
int p=pos[l],q=pos[r];
if(p==q)
{
for(re int i=l;i<=r;++i)
if(vis[i]) tmp=max(tmp,t*a[i].k+a[i].b); //暴力
}
else
{
for(re int i=l;i<=R[p];++i)
if(vis[i]) tmp=max(tmp,t*a[i].k+a[i].b);
for(re int i=L[q];i<=r;++i)
if(vis[i]) tmp=max(tmp,t*a[i].k+a[i].b);
for(re int i=p+1;i