WordBreak
给定一个字符串s和一个单词字典dict,确定是否可以将s分割成一个由一个或多个字典单词组成的空格分隔的序列。
s ="leetcode",
dict =["leet", "code"].
返回true,因为“leetcode”可以分割为“leetcode”。
bool isMatch(string s,unordered_set &dict)
{
if(dict.find(s) != dict.end())
return true;
return false;
}
bool wordBreak(string s, unordered_set &dict) {
if(dict.size() <= 0)
return false;
vector dp(s.length()+1,false);
dp[0] = true;//dp[k]表示从上一个dp true的位置开始到k-1这一字符串在dict中
for(int i = 0;i < s.length();++i)
{
for(int j = i;dp[i] && j < len;++j)//每次只针对当前j位置为true的情况才往下判断。
if(isMatch(s.substr(i,j-i+1),dict))
dp[j+1] = true;
}
return dp[s.length()];
}
给定一个单链表,其中元素按升序排序,将其转换为高度平衡的平衡二叉树。
分析:使用快慢指针,每次快指针指向链表最后一个结点或者快指针指向最后的NULL,就是该建立结点的时候,建立的结点是慢指针指向的结点,然后这个结点左边是左子树,右边是右子树,递归。
TreeNode* sortedListToBSTCore(ListNode *head,ListNode* tail)
{
if(head == tail)
return NULL;
ListNode* s;ListNode* f;
s = f = head;
while(f != tail && f->next != tail)
{
s = s->next;
f = f->next->next;
}
TreeNode* root = new TreeNode(s->val);
root->left = sortedListToBSTCore(head,s);
root->right = sortedListToBSTCore(s->next,tail);
return root;
}
TreeNode *sortedListToBST(ListNode *head) {
if(head == NULL)
return NULL;
return sortedListToBSTCore(head,NULL);
}
判断一棵树是不是二叉排序树
如果直接中序遍历来判断,会使用O(n)的空间。我们可以标记中序前一次遍历的结点,如果这个结点值比当前的大,那么一定不是二叉排序树。
但是一定要注意传参的方式!
bool isValidBSTCore(TreeNode* root,TreeNode **pre)
{
if(root == NULL)
return true;
bool ll = isValidBSTCore(root->left,pre);//传参方式
if(*pre&&root->val <= (*pre)->val)
return false;
*pre = root;
bool rr = isValidBSTCore(root->right,pre);//传参方式
return ll && rr;
}
bool isValidBST(TreeNode *root) {
TreeNode* pre = NULL;
return isValidBSTCore(root,&pre);//传参方式
}
如何构造一棵二叉排序树
void insertBST(TreeNode **root,int num)
{
if(!(*root))
{
*root = new TreeNode(num);
return;
}
if(num < (*root)->val)
insertBST(&(*root)->left,num);//(*root)->left指的是一个TreeNode指针,所以需要传引用
else
insertBST(&(*root)->right,num);
return;
}
void createTree(const vector &a,TreeNode **root)
{
for(int i = 0;i < a.size();++i)
insertBST(root,a[i]);//这里传递的与上边不同
return;
}
int main()
{
TreeNode* root;
createTree(a,&root);//这里传递的也是引用,与上边同理
}
正则表达式匹配
给定一个字符串 (s) 和一个字符模式 (p)。实现支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符。 '*' 匹配零个或多个前面的元素。
首先判断当前字符是否匹配,然后我们判断下一个字符是不是‘’,如果是,有两个选择:忽略当前字符或者多个当前字符(零个或多个),我们使用递归的||运算全部考虑进去。 如果下一个字符不是‘’,如果当前字符不匹配,那整个字符串就不匹配了,如果当前字符匹配,接着检查下一个。
class Solution {
public:
bool isMatchCore(const string &s,const string &p,char* p1,char* p2)
{
if(*p2 == '\0')
return *p1 == '\0';
bool last_match = (*p1 != '\0') && (*p1 == *p2 || *p2 == '.');//判断(*p1 != '\0')是因为有可能p1一直+1而p2不变。
if(*(p2+1) == '*')
return isMatchCore(s,p,p1,p2+2)||(last_match && isMatchCore(s,p,p1+1,p2));
else
return last_match && isMatchCore(s,p,p1+1,p2+1);
}
bool isMatch(string s, string p) {
char* p1 = &s[0];
char* p2 = &p[0];
return isMatchCore(s,p,p1,p2);
}
};
通配符匹配
给定一个字符串 (s) 和一个字符模式 (p) ,实现一个支持 '?' 和 '*' 的通配符匹配。
'?' 可以匹配任何单个字符。
'*' 可以匹配任意字符串(包括空字符串)。
s = "aa" p = "a" 输出: false s = "aa" p = "*" 输出: true
class Solution {
public:
bool isMatchCore(const string &s,const string &p,char* p1,char* p2)
{
if(*p2 == '\0')
return *p1 == '\0';
bool lastmatch = (*p1 != '\0')&&(*p1 == *p2 || *p2 == '?' || *p2 == '*');
if(*p2 == '*')
return isMatchCore(s,p,p1,p2+1)||(lastmatch && isMatchCore(s,p,p1+1,p2));
else
return lastmatch&&isMatchCore(s,p,p1+1,p2+1);
}
bool isMatch(string s, string p) {
char *p1 = &s[0];
char *p2 = &p[0];
return isMatchCore(s,p,p1,p2);
}
};
三数之和等于0
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
分析:在剑指offer中有一道题是求两数之和:
问题:输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的。
分析:这道题要求结果可以不是连续的。还可以使用上述双指针的方式,一个指针指向数组开头,一个指向结尾。若大了,尾指针前移,小了,头指针后移。
我们可以将本题目进行排序,然后遍历数组求出所有和为 -当前数 的数,也是使用双指针。但是在处理过程中,还要注意去重复,有三种出现重复的情况:1.必须从当前数的后边来找剩余的两个数。2.找到两个数之后,必须看看其左/右是不是还有重复的数。
vector> threeSum(vector& nums) {
vector> result;
int len = nums.size();
sort(nums.begin(),nums.end());
int i = 0,j = len-1;
for(int k = 0;k < len-2;++k)
{
if(k > 0 && nums[k] == nums[k-1])//这里还有一个防止重复的循环
continue;
i = k+1;//为什么从当前的数后边找?因为如果还是从0开始找,会有重复,-2 -1 -1 0 1 3,试一下
j = len-1;
while(i < j)
{
if(nums[i] + nums[j] < -nums[k])
i++;
else if(nums[i] + nums[j] > -nums[k])
j--;
else
{
vector temp;
temp.push_back(nums[k]);
temp.push_back(nums[i]);
temp.push_back(nums[j]);
result.push_back(temp);
i++;
j--;
while (nums[i] == nums[i - 1] && i < j)//防止重复
i++;
while (nums[j] == nums[j + 1] && i < j)//防止重复
j--;
}
}
}
return result;
}
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。同样使用这种方法。
int threeSumClosest(vector& nums, int target) {
int len = nums.size();
if(len < 3)
return 0;
sort(nums.begin(),nums.end());
int closeNum = nums[0] + nums[1] + nums[2];,threeNum;
for(int k = 0;k < len-2;++k)
{
int i = k+1;int j = len-1;//同上边解释
while(i < j)
{
threeNum = nums[i] + nums[j] + nums[k];
if(abs(threeNum-target) < abs(closeNum-target))
closeNum = threeNum;
if(threeNum - target > 0)
j--;
else if(threeNum - target < 0)
i++;
else
return threeNum;
}
}
return closeNum;
}
链表的排序(包含将两个有序链表合并成一个有序链表)
我们之前写过将两个有序链表合并成一个链表。所以如果对一个链表进行排序,可以使用归并排序的方法,这个方法的核心除了 将两个链表合并成一个链表之外,还有寻找中间结点。具体看下方算法。
ListNode* mergeTwoList(ListNode* l1,ListNode* l2)//将两个链表合并成一个链表
{
if(!l1)
return l2;
if(!l2)
return l1;
ListNode* head;
if(l1->val < l2->val)
{
head = l1;
head->next = mergeTwoList(l1->next,l2);
}
if(l1->val > l2->val)
{
head = l2;
head->next = mergeTwoList(l2->next,l1);
}
return head;
}
ListNode* findMid(ListNode* l)//寻找一个链表的中间结点,并将链表断开,中间节点在左边。返回的是右边那个链表
{
ListNode* p = l;ListNode* pfast = l;
while(pfast)
{
pfast = pfast->next;
if(pfast)
pfast = pfast->next;
if(!pfast)
break;
p = p->next;
}
ListNode* temp = p;
p = p->next;
temp->next = NULL;
return p;
}
ListNode* ParList(ListNode* head)
{
if(head == NULL || head->next == NULL)
return head;
ListNode* head1 = head;//head1指向递归中链表的头
ListNode* head2 = findMid(head);//head2指向递归中链表中间节点的下一个结点(即分开的链表右边链表的头)
head1 = ParList(head1);
head2 = ParList(head2);
return mergeTwoList(head1,head2);
}
下一个排列
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须原地修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1
其实就是从数组倒着查找,找到nums[i] 比nums[i+1]小的时候,就将nums[i]跟nums[i+1]到nums[nums.length - 1]当中找到一个最小的比nums[i]大的元素交换。交换后,再把nums[i+1]到nums[nums.length-1]排序,就ok了
void nextPermutation(vector& nums) {
if(nums.size() <= 1)
return;
int i,j,needswap,k;
for(j = nums.size()-1;j > 0;--j)
{
i = j-1;
if(nums[i] < nums[j])//i和后边比nums[i]大且最小的值交换
{
needswap = i+1;
for(k = i+1;k < nums.size();++k)//找到i后边比nums[i]大且最小的值交换
{
if(nums[k] < nums[needswap] && nums[k] > nums[i])
needswap = k;
}
swap(nums[i],nums[needswap]);
break;
}
}
if(j == 0)//如果所有的数字都比前一个数字大,逆置
{
reverse(nums.begin(),nums.end());
return;
}
sort(nums.begin()+i+1,nums.end());//将i之后的数字排序
}
反转单链表的递归写法
ListNode* reverse(ListNode* current,ListNode* pre)
{
if(current == NULL)
return pre;
ListNode* next = current->next;
current->next = pre;
return reverse(next,current);
}
ListNode* reverseList(ListNode* head) {
return reverse(head,NULL);
}
生成合法括号
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n = 3,生成结果为:["((()))", "(()())","(())()","()(())","()()()"]
分析:我们需要保证一点,在任何位置‘(’的个数总是总是大于等于‘)’的个数。所以加入‘)’的条件是 ll > rr
void generateParenthesisCore(vector &strs,string str,int ll,int rr,int n)
{
if(ll == n && rr == n)
{
strs.push_back(str);
return;
}
if(ll < n)
{
str += '(';
generateParenthesisCore(strs,str,ll+1,rr,n);//因为‘(’足够了才返回
str.pop_back();
}
if(ll > rr && rr < n)
{
str += ')';
generateParenthesisCore(strs,str,ll,rr+1,n);////因为‘)’足够了才返回
str.pop_back();
}
}
vector generateParenthesis(int n) {
vector strs;
string str;
generateParenthesisCore(strs,str,0,0,n);
return strs;
}
最长有效括号
输入: ")()())" 输出: 4 解释: 最长有效括号子串为 "()()"
分析:可以利用栈,进栈的不是字符而是字符下标。当遇见的字符是( ,下标直接进栈,如果遇见的是 ):先让栈顶元素出栈,假如栈中没有元素了,当前下标进栈,如果还有元素(说明有匹配),令当前下标减去栈顶元素得到的就是当前有效长度,至于是否是最长的,还得看接下来的计算。
其实我们一直在记录一个匹配的字符串左边那个字符,所以最开始要让-1先进栈。
int longestValidParentheses(string s) {
int len = s.length();
if(len <= 1)
return 0;
stack st;
st.push(-1);
int count = 0;
for(int i = 0;i < len;++i)
{
if(s[i] == '(')
st.push(i);
else
{
st.pop();//不管怎样,先pop栈顶元素,以此来寻找匹配的字符串左边那个字符下标,如果出栈后栈空了,
//表明当前 )没有匹配的( ,拿当前 )的下标作为匹配的字符串左边那个字符下标.
if(st.empty())
st.push(i);
else
count = max(count,i-st.top());
}
}
return count;
}
回溯法
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[[7],[2,2,3]]
本题目temp传引用更简单
void combinationSumCore(const vector& candidates, int target,vector &temp,vector> &result,int k)
{
if(target == 0)
{
result.push_back(temp);
return;
}
if(k == candidates.size() || candidates[k] > target)
{
return;
}
temp.push_back(candidates[k]);
combinationSumCore(candidates,target-candidates[k],temp,result,k);
temp.pop_back();
combinationSumCore(candidates,target,temp,result,k+1);//注意使用下一个数时target的取值。
}
vector> combinationSum(vector& candidates, int target) {
vector> result;
if(candidates.empty())
return result;
vector temp;
sort(candidates.begin(),candidates.end());
combinationSumCore(candidates,target,temp,result,0);
return result;
}
二叉树中和为某一值的路径
问题:输入一颗二叉树的跟节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中,数组长度大的数组靠前)
注意,temp传引用与不传引用都一样。
void findPathCore(TreeNode* root,int expectNumber,vector temp,vector> &result)
{
if(root == NULL)
return;
temp.push_back(root->val);
if(expectNumber == root->val && root->left == NULL && root->right == NULL)
{
result.push_back(temp);
}
if(expectNumber < 0)
return;
findPathCore(root->left,expectNumber-root->val,temp,result);
findPathCore(root->right,expectNumber-root->val,temp,result);
temp.pop_back();//如果是传引用,必须pop,如果不是传引用,pop不pop都一样
}
vector> FindPath(TreeNode* root,int expectNumber) {
vector> result;
vector temp;
findPathCore(root,expectNumber,temp,result);
return result;
}
动态规划背包问题
有1、2、5元面值的硬币,输入一个数,求有多少种兑换方法。
完全背包问题:兑换方法数 = 不取最后一种面值硬币的兑换方法数+取最后面值硬币的兑换方法数(必须使用最后的面值硬币)。
dp[i][j] = dp[i-1][j] + dp[i][j-value[i]].//当j-value[i] >= 0的时候,这样取,否则dp[i][j-value[i]]取0。
使用dp[i][j-value[i]]而不使用dp[i][j](使用最后面值硬币的兑换方法数)是因为二者值相同,这样能够把问题推到前边某一列。
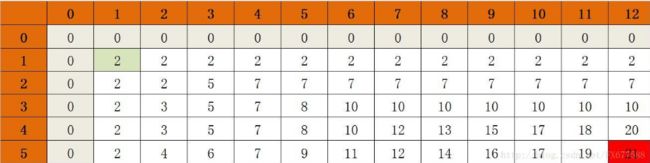
0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1//只使用1元,从1-10元的兑换方法
1 1 2 2 3 3 4 4 5 5 6//使用1元和两元
1 1 2 2 3 4 5 6 7 8 10//使用1元两元五元
第一行第一列是初始化的数字。第一行为0,第一列为1.这个例子是求10元有几种兑换方法。
int change(int amount, vector& coins) {
int len = coins.size();
if(amount == 0 || len <= 0)
return 0;
vector> a;
a.resize(len+1);
for(int i = 0;i < a.size();++i)
a[i].resize(5001);
for(int i = 0;i <= len;++i)
a[i][0] = 1;
for(int i = 0;i <= amount;++i)
a[0][i] = 0;
for(int i = 1;i <= len;++i)
{
for(int j = 1;j <= amount;++j)
{
int ss;
if(j - coins[i-1] >= 0)
ss = a[i][j-coins[i-1]];
else
ss = 0;
a[i][j] = a[i-1][j] + ss;
cout< 01背包问题:一般是求最大价值、最大热度等。
int nCost[6] = {0 , 2 , 5 , 3 , 10 , 4}; //价值
int nVol[6] = {0 , 1 , 3 , 2 , 6 , 2}; //物体体积
int bagV = 12;//背包体积。
if(j else 注意刚开始第一行第一列都为0 [图片上传失败...(image-eb5abe-1560669495939)] 给定一个整数 n,求以 1 ... n 为节点组成的二叉搜索树有多少种? 输入: 3 输出: 5 给定 n = 3, 一共有 5 种不同结构的二叉搜索树: 分析: 输入n,分为以1为根结点情况,以2为根结点情况......以n为根结点情况。假设n = 3: 以1为根结点,左子树只有一种情况为NULL(dp[0]),右子树有dp[3-1]种情况,即n==2时有几种情况。 以2为根结点,左子树有dp[1]种情况,即n==1时有几种情况。右子树有dp[3-2]种情况,即n == 1时有几种情况。 以3为根结点,左子树有dp[2]种情况,即n==2时有几种情况。右子树有dp[3-3]种情况。 所以公式为 dp[n] = dp[0]dp[n-1] + dp[1]dp[n-2] + dp[2]dp[n-3] + dp[n-1]dp[0];nArr[i][j] = nArr[i-1][j];
nArr[i][j] = max(nArr[i-1][j] , nArr[i-1][j-nVol[i]] + nCost[i]);//价值=不取当前体积的物体情况下的价值 与 必须取当前体积物体情况下的价 值 二者的最大值。
动态规划求二叉搜索树个数
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
int numTrees(int n) {
if(n <= 0)
return 0;
vector