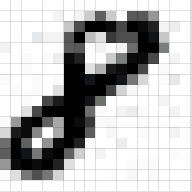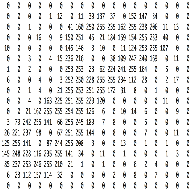An Intuitive Explanation of Convolutional Neural Networks
原文地址:https://ujjwalkarn.me/2016/08/11/intuitive-explanation-convnets/comment-page-4/?unapproved=31867&moderation-hash=1ac28e426bc9919dc1a295563f9c60ae#comment-31867
一、什么是卷积神经网络、为什么卷积神经网络很重要?
卷积神经网络
图 1: 来源 [1]
在上图 图1 中ConvNet 可以识别场景并且系统可以建立相关关联(“一个足球运动员在踢足球”),然而在下图 图2 的示例中展示了ConvNets 用于识别物体、人和动物。最近,ConvNets 在某些自然语言处理任务(例如句子分类)中也有效。[ 注:微软小冰、苹果Siri 等,读者也可以调用微软AI搭建自己的应用程序。译者加]
图 2: 来源 [2]
因此,ConvNets 对于大多机器学习从业者来说是一个很重要的工具。 然而有时候对于首次理解ConvNets、学习使用ConvNets 来说可能令人生畏。本博客主要目的是加深理解 ConvNet 如何处理图片。
通常来说如果你对神经网络不熟悉,我推荐在继续阅读之前 阅读 this short tutorial on Multi Layer Perceptrons 以熟悉了解 ConvNe t的工作原理。多层感知器在本文中称为 “Fully Connected Layers” 。
二、LeNet 结构(1990年)
LeNet 是最早推动深度学习领域的卷积神经网络之一。这项开创性工作自1988年[3]以来,在多次迭代成功之后被 Yann LeCun 命名为 LeNet5 . 在当时 LeNet 结构主要被用于字符任务,比如读取邮政编码、数字等。
下面,我门将直观的介绍 LeNet结构 学习如何识别图像。近年来有几种新的体系结构对 LeNet 进行了改进,然而它们都使用了LeNet 的主要概念,如果你对LeNet 有清晰的理解,则相对容易理解以下内容。
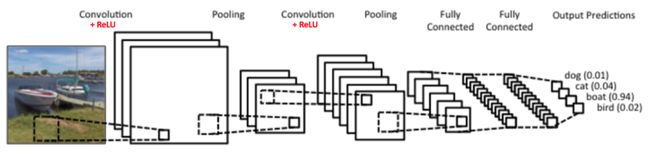
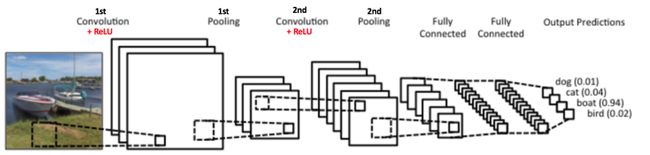
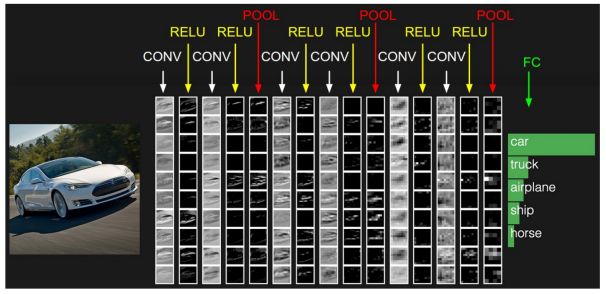
图 3: 一个简单卷积神经网络. 来源[5]
图3 中的卷积神经网络在结构上与原始LeNet 类似,有四个输入分类:狗、猫、船和鸟(原始LeNet 主要用于字符识别任务)。从上图明显可以看出,在得到一个船的图片作为输入,该网络在所有分类中正确的标记最高的可能性为船(0.94)。输出层中所有输出可能性之和应该为1.(稍后解释为什么总和应该为1)
以上图3 显示了 ConvNet 中的4个主要操作。
1、卷积 - Convolution
2、非线性 - ReLU
3、池化 - Pooling
4、分类 - Classification
每一个卷积神经网络都包含了这些基本构筑块,因此理解以上步骤原理,对于理解ConvNet 是非常重要的一步。我们将在下面尝试直观的理解这些步骤背后的操作。
三、图像 - 一个像素矩阵
本质上,每一个图片都能用一个像素矩阵表示。 [注:这是ConvNet 的基础 。译者加]
图4: 图片-像素矩阵. 来源[6]
通道-Channel 是用于指代图片某一部分的常规术语。标准数码相机中的图像具有3个通道 红、绿、蓝,可以想象为3个2维矩阵的叠加(每种颜色一矩阵),每一个像素值在0到255之间,包含0和255。
灰度图-grayscale 只有一个通道。出于本文目的,我们将只考虑灰度图像,因此我们将一个二维矩阵代表一个图片。矩阵中的每一个值都在0到255之间,0 表示黑色,255 表示 白色 。
四、卷积步骤
ConvNet 得名于它的 “卷积-convolution” 操作。对于 ConvNet 来说,卷积操作主要是为了从输入图像中提取特征。卷积通过使用输入数据的小方块学习图像特征,保留像素之间的空间关系。在这里我们不讨论卷积的具体数学原理,只是了解卷积在图像处理上的原理。
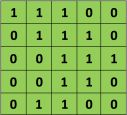
如上述讨论,每一个图片都可视为一个像素矩阵。如下一个 5 * 5 的图像,像素值只包含0 和 1 (注:对于灰度图,像素值在0到255,下图是一个特例仅包含0和1):
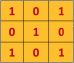
同时,考虑另外一个 3 * 3 矩阵 如下图所示:
然后,可以计算出 5 * 5 图像 和 3 * 3 矩阵卷积结果,如下动图 图5 所示:
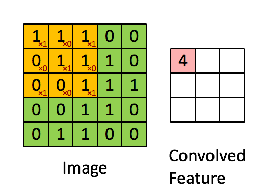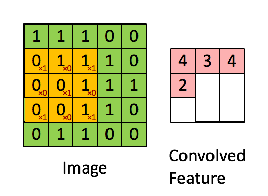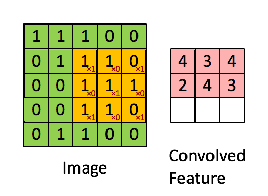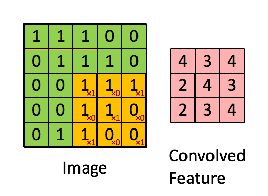
图 5: 卷积操作. 来源[7]
花点时间理解一下上面卷积过程的计算是如何完成的。我们将橙色矩阵在原始图像(绿色)上滑动一个像素(也成为“跨度”),针对每一个位置我们计算元素的“wise”乘法(两个矩阵之间)然后将乘法输出相加获取最终的整数结果,该结果作为输出矩阵的单个元素(粉红色矩阵)。请注意, 每一步中 3 * 3 矩阵仅仅是输入图像的一分部。
3 * 3 矩阵,在 CNN 术语中被称为:“过滤器-filter” 或 “内核-kernel” 或 “特征检测器-feature detector”;通过在原始图上滑动 “过滤器-filter” 并计算点积所形成的矩阵称为:“卷积特征-Convolved Feature” 或 “激活图-Activation Map” 或 “特征图-Feature Map”。请注意,在原始输入图像中过滤行为作为特征检测非常重要。
从上面的动画图可以看出,对于同一个输入图像,不同的过滤矩阵产生不同的特征图。例如,考虑以下输入图像:
在下图表中,我们可以看到使用不同的过滤器在图上的卷积效果。如图所示,在卷积操作[8]之前我们可以通过改变过滤器矩阵的数值执行操诸如 边缘检测-Edge Detection、锐化-Sharpen和模糊-Blur 之类的操作,这意味着不同的滤镜可以检测图像中的不同特征,例如边缘、曲线等。更多的此类示例可以在8.2.4 节获取。[注:https://docs.gimp.org/en/plug-in-convmatrix.html 链接Not Found ,译者加]
也可以通过下图 图6 动画所示,直观的理解卷积操作。
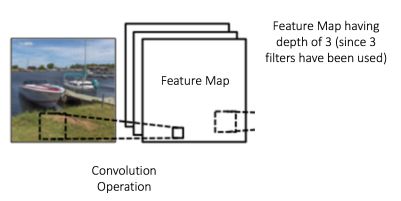
图 6: 卷积操作. 来源[9]
一个过滤器(红色轮廓矩形)划过输入图像(卷积操作)产生一个特征图。如图,卷积操作的另外一个过滤器(绿色轮廓矩形)在同一张图上得到了一个不同的特征图。特别注意,卷积操作会捕获原图像中的局部依赖。同时也要注意,这两个不同的过滤器如何从同一张原始图像中生成不同的特征图。记住,我么讨论的前提是,原始图像和两个过滤器都是数字矩阵。
实际上,CNN 在训练过程中会自行学习这些过滤器的值(尽管如此,在训练模型之前我们仍需要指定参数例如:过滤器数量、过滤器大小、网络结构等)。过滤器越多,将会提取到越多的图像特征,这样我们的网络在识别未知图像时更有效。
特征图(卷积特征)的大小取决于执行卷积步骤前确定的 3 个参数[4] :
• 深度-Depth : 深度对应我们用于卷积操作的滤波器数量。 图7 所示神经网络中,我们在原始图像中使用 3 个不同的过滤器,因此产生了三个不同的特征图。你可将这 3 个特征图想象为堆叠的 2 维矩阵,因此 该特征图的深度就是 3。
图 7
• 跨度-Stride: 跨度就是我们的过滤矩阵每次划过原始输入矩阵的像素数。当跨度为 1 时,我们的过滤器每次移动一个像素。当跨度为 2 时,此时过滤器每次滑动跳过两个像素。跨度较大产生的特征图较小。
• 零填充-Zero-padding: 有时候,使用 0 填充输入矩阵的边界非常方便,因此我们可以应用过滤器作为输入图像矩阵的边界元素。Zero-padding 一个优点就是允许我们控制特征图的大小。添加 Zero-padding 也成为宽卷积,反之不使用 Zero-padding 称为 窄卷积。在 [14] 中对此作了明确的解释。
五、ReLu 介绍
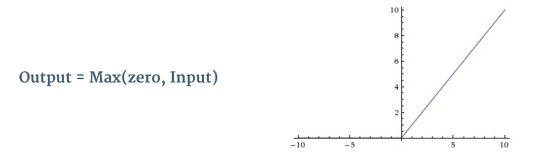
在上面 图3 中每一次卷积操作之后都使用了一个叫 ReLu 的附加操作。ReLU 代表 Rectified Linear Unit ,它是非线性操作。它的输出如下图:
图8: ReLU 操作
ReLu 是一个元素 “wise operation”(应用于每一个像素),在特征图中将负像素全部替换为零。ReLU 的目的是在我们的 ConVNet 中引入非线性,因为大多数真实世界中的数据,因此我们希望 ConvNet 学习是非线性的(卷积操作是 “element wise” 的矩阵乘法和加法 属于线性操作 ,因此我们引入如ReLU之类的非线性函数解决非线性问题)。
下图 图9 可以明了的理解 ReLU 操作。它展示了上图 图6中获取特征图之一的 ReLU 操作。要输出的特征图 在这里也被称为 “Rectified” 特征图 。
图9: ReLU 操作. 来源[10]
可以使用其它非线性函数例如:tanh 、sigmoid 替代 ReLU ,然而 ReLU 被发现在大多数场景下表现更为出色。
六、池化
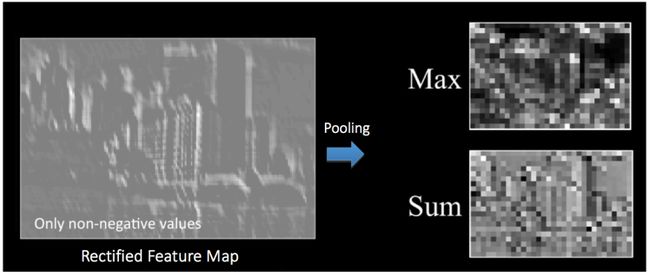
空间池化(也称子采样或向下采样) 降低了每个特征图的维度同时保留了最重要信息。空间池化有不同的类型:Max、Average、Sum 等。
在 Max pooling 中,我们定义了一个空间邻域(例如:2 * 2 区域)在该空间邻域内校正后的特征图中获取最大值。除了获取该邻域的最大元素值,我们也可以获取平均值(Average Pooling)或 总和。在实践中, Max Pooling 表现的更为出色 。
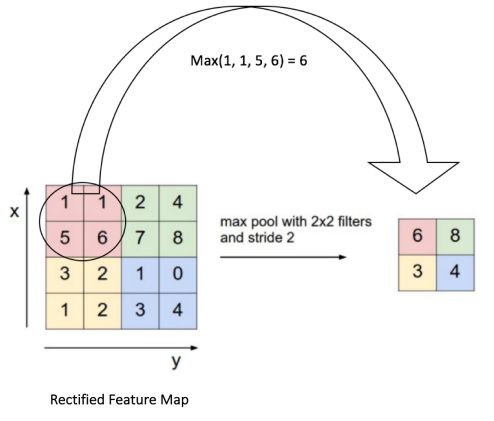
图 10 中展示了在“校正特征图-Rectified Feature map”(卷积操作+ReLU 操作) 上使用 2 * 2 过滤器的 Max Pooling 操作。
图 10: Max Pooling. 来源[4]
我们每次滑动 2 * 2 过滤器 2小格(也称“跨度”),同时取出每个区域的最大值。如 图 10 所示,Max Pooling 操作会降低特征图的维度。
下图 图11 所示的神经网络中,池化操作应用于每个不同的特征图(注意因此,从三个输入图 得到三个输出图)。
图11: 校正特征图-Rectified Feature Maps 池化
图 12 展示了池化操作对 图9 进行ReLU 操作后校正特征图-Rectified Feature Map 的作用结果。
图12: 池化. 来源[10]
池化的作用是逐渐减少输入维度的大小[4]。池化有以下要点:
• 使输入描述- input representations(特征尺寸)更小且易于管理-more manageable。
• 减少神经网络中的参数和计算量,因此,要注意控制过拟合-Overfitting[4]。
• 使网络中对输入图像中 降维-small transformations、失真-distortions、平移-translations保持不变(我们获取领域中的 最大/平均值,因此输入中的少量失真不会改变池化输出)。
• 帮助我们获取图像的几乎不变的不变表示(“等变-equivariant”)。这对我们检测到图像中的任意地方的对象非常有用(详情阅读[18] 和[19])。
七、小结-Story so far
图 13
截止目前为止,我们已经了解了 卷积、ReLU、池化的工作原理。这对我们理解任意 CNN(卷积神经网络)的基本构造块和层非常有用。如 图13 所示我们有2组 卷积、ReLU 和池化层,第二个卷积层对第一个池化层的输出使用6个过滤器产生六个特征图;然后,ReLU 作用于第二层卷积输出的6个特征图;然后我们使用 Max Pooling 操作上步骤处理之后的6个校正特征图- rectified feature maps。
这些层组合在一起,对于从图像中提取特征非常有用,在神经网路中引用非线性-non-linearity和减小特征尺度,同时旨在有些特征在进行缩放和平移时保持等变[18]。
我们将在下一节讨论,第二个池化层的输出充当完全连接层-Fully Connected Layer的输入。
八、完全连接层-Fully Connected layer
完全连接层是一个传统的多层感知器,在输出层使用 softmax 激活函数(也可以使用诸如 SVM 的分离器,然而本文使用 softmax)。术语“Fully Connected” 意味着上层的每个神经元都连接到下一层的每个神经元。如果你对多层感知器不熟悉,推荐阅读 A Quick Introduction to Neural Networks 。
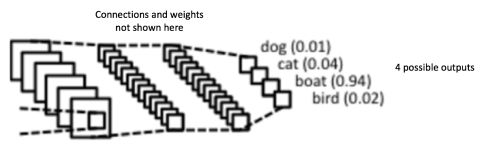
卷积和池化层的输出代表输入图像的高层次特征-high-level features。完全连接层的作用是根据训练集的这些特征将输入图像进行分类。例如,图14 展示我们执行图像分类任务有四个可能的输出(请注意,图14没有展示完全连接层之间的节点链接)。
图 14: 完全连接层的每个节点都连接到相邻层每个节点
除了分类问题,添加一个完全连接层是通常一种廉价的方式去学习组合这些非线性特征。卷积和池化层得到的大多数特征也许有助于分类任务,但是将这些特征进行组合也许会获取更好的结果[11]。
完全连接层输出的概率总和为 1 ,这确保了完全连接层作为输出层使用 Softmax 激活函数。Softmax 函数接受任意实数分数向量并且压缩它的向量值在 0 和 1 之间 总和为 1.
九、放在一起-使用反向传播训练 Putting it all together – Training using Backpropagation
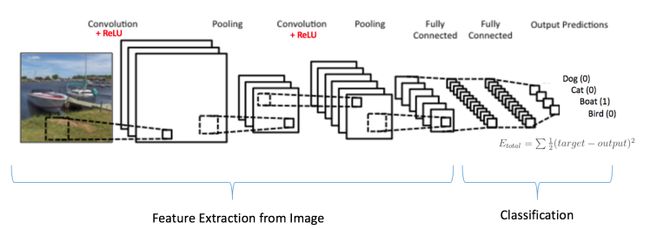
由以上讨论可以得出,卷积和池化层充当输入图像特征提取器,完全连接层充当分类器。请注意下图 图15中,由于输入图像是船,船的目标概率是 1 其它三类的概率为 0 。
• 输入图像 = 船
• 目标矢量 = [0,0,1,0]
图15: 训练 ConvNet
卷积神经网络的训练过程总结如下:
• Step1: 使用随机值初始化所有的过滤器、参数、权重
• Step2: 网络使用训练图像作为输入,经过向前传播步骤(卷积、ReLU、池化操作以及完全连接层中的向前传播)并找到每个类别的输出概率。
• 可以说上面船图像的输出概率为 [0.2,0.4,0.1,0.3]
• 由于第一次训练样本分配的是随机权重,因此输出概率也是随机。
• Step3: 计算输出层的总误差(所有4个分类之和)
• Total Error = ∑ ½ (target probability – output probability) ²
• Step4: 使用反向传播-Backpropagation 在网络中计算所有权重的梯度误差,并且使用 梯度下降更新所有的过滤器、权重、参数值使得输出误差最小。
• 根据对总误差的贡献大小调整权重。
• 当再次使用同一个输入图像,输出概率现在可能是 [0.1,0.1,0.7,0.1],输出概率接近于目标矢量[0,0,1,0]。
• 这意味着网络已经学会通过调整它的权重、过滤器、正确分类特定图像,从而减小输出误差。
• 训练过程中网络参数过滤器数量、过滤器大小、网络结构等,都在步骤1中已确定不会改变,只有过滤器矩阵的值和连接权重会更新。
• Step5: 对训练集中的所有图像重复步骤2-4 。
上面的训练 ConvNet 的步骤,意味着 ConvNet 所有的权重参数现已经经过优化,可以对训练集中的图像进行正确的分类。
当一个新图像(未经过训练)输入到 ConvNet ,网络将通过向前传播步骤并且输出每个类别的概率(对于新图像,网络使用之前训练样本优化过的权重计算输出概率)。如果你的训练集足够大,网络将对新图像 友好-generalize well 并将它们正确的分类。
注 1:上面的步骤已经经过简化并且隐藏了数学细节,对训练过程提供一个直观理解。有关数学公式及更深刻的理解查看[4] 和[12] 。
注 2:上面的例子中我们使用了两组交替的卷积和池化层。请注意在单个 ConvNet 中这些操作都可重复若干次。事实上,当前一些表现良好的 ConvNets 存在数十个 卷积和池化层。每个卷积层之后不一定要存在一个池化层。从下图 图16 可以看出,在进行一次池化操作之前我们可以连续使用多个卷积和 ReLU 操作。同时注意 下图 图16中 ConVNet 每一层的可视化。
图16: 来源[4]
十、卷积神经网络可视化-Visualizing Convolutional Neural Networks
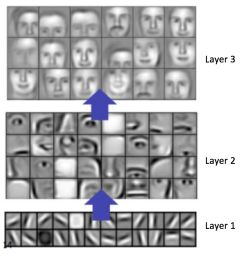
一般来说,更多的卷积步骤,意味着网络可以学习识别更多复杂的特征。例如,图像分类中一个 ConvNet 在第一层从原始像素中可以学习边缘检测-detect edges ,然后使用边缘在第二层检测简单形状,然后使用这些形状图确定高层次特征,比如较高层中的面部形状[14]。如下图17所示,这些使用 Convolutional Deep Belief Network 学习这些特征,此图在这里仅仅为了展示这个思想(这仅仅是一个例子:实际上卷积过滤器检测到的对象可能毫无意义)。
图17: 从 Convolutional Deep Belief Network 学习特征. 来源[21]
Adam Harley 在训练MNIST手写数字集卷积神经网络时,创造了惊人的可视化效果 [13]。强烈建议使用playing around 理解CNN 的工作原理。
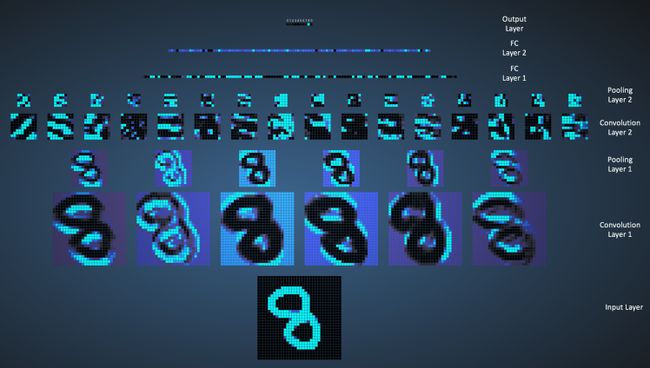
我们可以看到网络对于输入“8”的处理方式。注意图18可视化未单独展示ReLU操作。
图18: 可视化 ConvNet 训练手写数字. 来源[13]
输入图像包含 1024 个像素(32 * 32 图片), 6 个 5 * 5(跨度1) 过滤器卷积输入图像形成第一个卷积层。可以看出,使用 6 个不同的过滤器产生深度为 6 的特征图。
卷积层1 之后是池化层,池化层 使用 2 * 2 max pooling(跨度为2)分别作用于卷积层1中的 6 个特征图。你可以在池化层中的任意移动鼠标指针,在前一个卷积层观察 2 * 2 的小格(如图19所示)。你会注意到 2 * 2 小格的最大像素值被填充到池化层。
图19: 可视化Pooling 操作. 来源[13]
第一个池化层之后 使用了 16 个 5 * 5 (跨度 1)卷积过滤器执行卷积操作。接下来对第二层进行 2 * 2 max pooling(跨度 2)池化操作。 这两层使用了与上述相同的概念。
此时我们有三个完全连接层(FC)。它们是:
• 第一层完全连接层,具有 120 个神经元
• 第二层完全连接层,具有 100 个神经元
• 第三层完全连接层,具有 10 个神经元对应 10 个数字,也称输出层
观察下图 图20 中的方式,输出层 10 个节点的每一个节点都连接 第二层完全连接层的所有 100 个节点(因此,命名为全连接)。
同时注意,输出层的唯一亮点怎样与 “8” 对应,这意味着我们的网络对手写数字进行了正确分类(较亮的的节点表示较高的输出,也就是说 8 在所有数字中有最高的概率)。
图20: 可视化完全连接层. 来源[13]
此处提供了相同可视化的 3D 版本 here 。
十一、 其它 convNet 结构
卷积神经网络最早可追溯到 1990年。以上我们讨论的 LeNet 属于最早的神经网络之一。下面罗列了一些其它有影响的网络结构[3] [4]。
• LeNet (1990年):本文已经介绍。
• 1990 到2012年:自从1990 年以后到2010年早些时候卷积神经网络得到了发展。随着可用越来越多的数据量和强大的计算能力,卷积神经网络可以解决的任务越来越有趣。
• AlexNet (2012):在2012年,Alex Krizhevsky (和其他人)发布了 AlexNet ,该网络是在 LeNet 基础上更深更广的版本,并且在2012年赢得了 ImageNet 大规模视觉识别挑战赛(ILSVRC)。与以前的网络相比这是里程碑式的突破,当前 CNN 的广泛应用都可以归功于此项工作。
• ZF Net (2013):Matthew Zeiler 和 Rob Fergus 的卷积神经网络 赢得了2013年的ILSVRC 。它被称为 ZFNet(Zeiler 和 Fergus Net的简写)。通过对 AlexNet 超参数的调整提升该网络。
• GoogLeNet (2014):2014年ILSVRC 的赢得这是来自谷歌Szegedy等人的卷积神经网络。它的主要是贡献是开发了一个 Inception 模块,该模块大大减少了网络中的参数数量(相比较AlexNet 的60M 它只有4M)。
• VGGNet (2014):VGGNet 赢得了2014年 ILSVRC 的亚军。它的主要贡献是表明网络深度(层数)是获得良好性能的关键要素。
• ResNets (2015):Kaiming He (和其他人) 开发的 Residual Network 赢得了2015年的 ILSVRC 。ResNets 是目前最先进的卷积神经网络模型,实践中默认使用的 ConvNets 模型(截止2016年5月)。
• DenseNet (August 2016) :最近由Gao Huang (和其他人)发布的 Densely Connected Convolutional Network,该网络使用前馈的方式直接连接到其它每一层。事实证明,DenseNet在先前最新先进架构识别五个高度竞争对象的基准任务上有显著提升。此处查看Torch 的实现 here 。
十二、结论
本文中,我试图使用简单的术语解释卷积神经网络的主要概念。这里简化、跳过了一些细节,但是希望本文能让你直观的理解它们如何工作。
本文最初由Denny Britz的《Understanding Convolutional Neural Networks for NLP》(推荐阅读)启发而来,这里许多解释都源于该文章。为了更深入理解这些概念,鼓励你体验 斯坦福 ConvNets课程 笔记 以及下面参考文献中的有些资源。如果你理解上述概念遇到任何问题或者 有问题或建议,随时在下面发表评论。
该文所引用到的图片动图均属于原作者,如以下参考文献所罗列。
十三、参考文献
- karpathy/neuraltalk2: Efficient Image Captioning code in Torch, Examples
- Shaoqing Ren, et al, “Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks”, 2015, arXiv:1506.01497
- Neural Network Architectures, Eugenio Culurciello’s blog
- CS231n Convolutional Neural Networks for Visual Recognition, Stanford
- Clarifai / Technology
- Machine Learning is Fun! Part 3: Deep Learning and Convolutional Neural Networks
- Feature extraction using convolution, Stanford
- Wikipedia article on Kernel (image processing)
- Deep Learning Methods for Vision, CVPR 2012 Tutorial
- Neural Networks by Rob Fergus, Machine Learning Summer School 2015
- What do the fully connected layers do in CNNs?
- Convolutional Neural Networks, Andrew Gibiansky
- A. W. Harley, “An Interactive Node-Link Visualization of Convolutional Neural Networks,” in ISVC, pages 867-877, 2015 (link). Demo
- Understanding Convolutional Neural Networks for NLP
- Backpropagation in Convolutional Neural Networks
- A Beginner’s Guide To Understanding Convolutional Neural Networks
- Vincent Dumoulin, et al, “A guide to convolution arithmetic for deep learning”, 2015, arXiv:1603.07285
- What is the difference between deep learning and usual machine learning?
- How is a convolutional neural network able to learn invariant features?
- A Taxonomy of Deep Convolutional Neural Nets for Computer Vision
- Honglak Lee, et al, “Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations” (link)