粒子群算法属于智慧算法的一类,与该类算法类似的还有蚁群算法,遗传算法等。大家可以将这几种算法进行比较。
粒子群优化算法(Particle Swarm Optimization,PSO)属于进化算法的一种,是通过模拟鸟群捕食行为设计的。从随机解出发,通过迭代寻找最优解,通过适应度来评价解的品质。在这里,我们举一个例子来深入理解一下该算法:假设有一鸟群,在一座岛上某个地方放有食物,但是鸟群并不知道食物在哪,只是知道与食物之间的距离。这时候鸟儿们很聪明,它们在目前距离食物最近的鸟的周围搜索。
所有的粒子具有一下两个属性:
位置v
速度x
PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代种,粒子通过跟踪两个“极值”来跟新自己。第一个就是粒子本身所找到的最优解pbest;另一个极值是整个种群目前找到的最优解,及全局极值gbest。粒子通过下面的公式来更新自己速度和位置:
速度变换公式:
vi+1=w∗vi+c1∗rand1∗(pbesti−xi)+c2∗rand2∗(gbesti−xi)v_{i+1}=w*v_i+c_1*rand_1*(pbest_i-x_i)+c_2*rand_2*(gbest_i-x_i)vi+1=w∗vi+c1∗rand1∗(pbesti−xi)+c2∗rand2∗(gbesti−xi)
位置变换公式:
xi=xi+vi+1x_i=x_i+v_{i+1}xi=xi+vi+1
以上式子中:
w为惯性因子,一般取1
c1,c2c_1,c_2c1,c2为学习因子,一般取2
rand1,rand2rand_1,rand_2rand1,rand2为(0,1)之间的随机数
vi和xiv_i和x_ivi和xi分别表示粒子第i维的速度和位置
pbesti,,gbestipbest_i,,gbest_ipbesti,,gbesti分别表示某个粒子最好位置第i维的值,整个种群最好位置第i维的值
注意:以上两式是针对粒子的某一个维度进行跟新的。对粒子的每一维,都要用上述的式子进行更新。
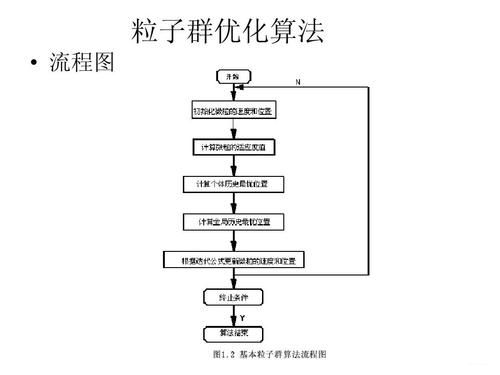
流程图如下:
# coding: utf-8
import numpy as np
import random
import matplotlib.pyplot as plt
class PSO():
# PSO参数设置
def __init__(self, pN, dim, max_iter):
self.w = 0.8
self.c1 = 2
self.c2 = 2
self.r1 = 0.6
self.r2 = 0.3
self.pN = pN # 粒子数量
self.dim = dim # 搜索维度
self.max_iter = max_iter # 迭代次数
self.X = np.zeros((self.pN, self.dim)) # 所有粒子的位置和速度
self.V = np.zeros((self.pN, self.dim))
self.pbest = np.zeros((self.pN, self.dim)) # 个体经历的最佳位置和全局最佳位置
self.gbest = np.zeros((1, self.dim))
self.p_fit = np.zeros(self.pN) # 每个个体的历史最佳适应值
self.fit = 1e10 # 全局最佳适应值
#目标函数Sphere函数
def function(self, X):
return X**4-2*X+3
#初始化种群
def init_Population(self):
for i in range(self.pN):
for j in range(self.dim):
self.X[i][j] = random.uniform(0, 1)
self.V[i][j] = random.uniform(0, 1)
self.pbest[i] = self.X[i]
tmp = self.function(self.X[i])
self.p_fit[i] = tmp
if tmp < self.fit:
self.fit = tmp
self.gbest = self.X[i]
# 更新粒子位置
def iterator(self):
fitness = []无锡×××医院 https://yyk.familydoctor.com.cn/20612/
for t in range(self.max_iter):
for i in range(self.pN): # 更新gbest\pbest
temp = self.function(self.X[i])
if temp < self.p_fit[i]: # 更新个体最优
self.p_fit[i] = temp
self.pbest[i] = self.X[i]
if self.p_fit[i] < self.fit: # 更新全局最优
self.gbest = self.X[i]
self.fit = self.p_fit[i]
for i in range(self.pN):
self.V[i] = self.w * self.V[i] + self.c1 * self.r1 * (self.pbest[i] - self.X[i]) + \
self.c2 * self.r2 * (self.gbest - self.X[i])
self.X[i] = self.X[i] + self.V[i]
fitness.append(self.fit)
print(self.X[0], end=" ")
print(self.fit) # 输出最优值
return fitness
加入下列代码验证结果:
#程序
my_pso = PSO(pN=30, dim=1, max_iter=100)
my_pso.init_Population()
fitness = my_pso.iterator()
# 画图
plt.figure(1)
plt.title("Figure1")
plt.xlabel("iterators", size=14)
plt.ylabel("fitness", size=14)
t = np.array([t for t in range(0, 100)])
fitness = np.array(fitness)
plt.plot(t, fitness, color='b', linewidth=3)
plt.show()
在上面我们计算X4−2X+3X^4-2X+3X4−2X+3的优化函数。
得出结果:
1.迭代图像
2.迭代最后的结果可以看出来在x取0.1937左右,X4−2X+3X^4-2X+3X4−2X+3取得较优值