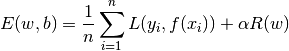原文章为scikit-learn中"用户指南"-->"监督学习的第五节：Stochastic Gradient Descent"######

**随机梯度下降(SGD) 是一个既有效又简单的方法去用于在诸如（线性）支持向量机和 Logistic回归中，"凸"代价函数下的线性分类器的辨别学习。尽管 SGD **已经在机器学习社区存在了很长一段时间了，但是在最近的大规模学习的浪潮下它还是得到了很多人的关注。

SGD 已经很成功的应用在了大规模下和稀疏机器学习问题上，主要是用于进行文本分类和自然语言处理。对给定一个稀疏的数据，（Sklearn）中的分类器能够很容易的扩展为能够处理超过10^{5个训练样本和超过10}5个特征的问题。

**SGD **的优点有：

极其效率。
易于实施（有大量调整代码的余地）。

但是其缺点有：

需要许多超参数，例如正则化参数和迭代次数。
对数据缩放很敏感。

1.5.1. 分类#

注意：请确保在每次拟合模型之前都对数据进行重新排序，不然则设置 shuffle=True 使得在每次迭代中都会重排数据。

类 SGDClassifier
实现了一个常规的朴素梯度下降学习，其对分类问题支持许多不同的代价函数和惩罚项。

一个SGD分类的实例

跟其他分类器一样，**SGD 同样需要拟合两个数组：一个保存着训练样本，尺寸为 [n_samples, n_features] 的数组 X 和一个保存着结果标签，尺寸为 [n_samples] 的数组 y **：

>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = SGDClassifier(loss="hinge", penalty="l2")
>>> clf.fit(X, y)
SGDClassifier(alpha=0.0001, average=False, class_weight=None, epsilon=0.1,
       eta0=0.0, fit_intercept=True, l1_ratio=0.15,
       learning_rate='optimal', loss='hinge', n_iter=5, n_jobs=1,
       penalty='l2', power_t=0.5, random_state=None, shuffle=True,
       verbose=0, warm_start=False)

在拟合之后，这个模型就可以用来预测了：

>>> clf.predict([[2., 2.]])
array([1])

**SGD 使用训练集拟合了一个线性模型，其成员 coef_ **保存着模型参数：

>>> clf.coef_                                         
array([[ 9.9...,  9.9...]])

然后成员** intercept_ **保存着截距（也称为偏移值或偏差）

>>> clf.intercept_                                    
array([-9.9...])

不用关心模型是不是用了截距，其超平面截距，都是由** fit_intercept **参数控制。

可以通过 SGDClassifier.decision_function
来获得超平面的带符号距离：

>>> clf.decision_function([[2., 2.]])                 
array([ 29.6...])

可以通过** loss **参数来选择具体是要使用哪个代价函数。SGDClassifier
支持以下几种代价函数：

loss="hinge": (软边际) 线性支持向量机,
loss="modified_huber": 平滑的 hinge 代价函数,
loss="log": logistic回归,
和下方"回归"一节中的代价函数.

前面两种代价函数是懒惰的，他们只在样本违反了边际的约束（即出现意外值时）才会更新模型参数，也因为如此在训练的时候很执行效率很高，但也同样会使得产生出不同稀疏模型，即便是使用了L2惩罚项。

设置** loss="log" ** 或 ** loss="modified_huber" 来启用 predict_proba 函数，这个函数对于每个样本 x 都会给出估计概率( P(y | x) **)矩阵。

>>> clf = SGDClassifier(loss="log").fit(X, y)
>>> clf.predict_proba([[1., 1.]])                      
array([[ 0.00...,  0.99...]])

可以通过** penalty 参数来选择需要使用哪种惩罚项，SGD **支持下列几种：

penalty="l2": 使用L2范数对** coef_ **进行惩罚。
penalty="l1": 使用L1范数对** coef_ **进行惩罚。
penalty="elasticnet": 使用L2和L1的凸组合： (1 - l1_ratio) * L2 + l1_ratio * L1 对** coef_ **进行惩罚。

**SGD 的默认惩罚项是 penalty="l2" ，使用L1惩罚项会生成出一个大多数系数为零的稀疏模型。若使用弹性网络则会解决一些L1惩罚在高度相关属性中存在的缺陷。参数 l1_ratio **控制着L2与L2惩罚项的凸组合。

SGDClassifier
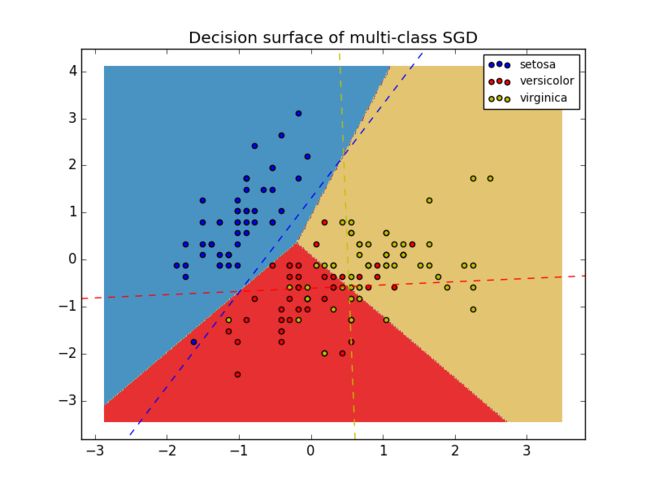
能够在“一对多” (OVA)方案下，通过组合多个二元分类器来进行多类分类。对于每一个K类，二元分类器会比较其与** K-1 **类的区别进行学习。在测试阶段，我们为每一个分类器计算其置信度（即到超平面的带符号距离），然后选择具有高置信度的类。下方的图表表现了OVA在鸢尾花数据集中的表现。虚线代表着三种OVA分类器；背景颜色则表现了这三个分类器的决策边界。

三种OVA分类器在iris数据集的表现

在多类分类情况，**coef_ 是一个形状为 [n_classes, n_features] 的二维数组，然后 intercept_ 是一个形状为 [n_classes] 的一维数组。然后对第 i 行的 coef_ 而言，其保存着第 i 类的分类器的权重向量。然后类是按升序来索引的（可以查看 classes_ 属性）。但要注意的是，因为在原则上这个多类分类器是允许创建出一个概率模型的，所以最好设置代价函数为 loss="log" 或 loss="modified_huber" **，这样做比使用默认的代价函数要更适合这个一对多分类。

SGDClassifier
能通过** fit 参数 class_weight 和 sample_weight **支持权重类和权重实例。要了解更多的内容可以查看下面的例子或是这个类的说明文档 SGDClassifier.fit
。

示例

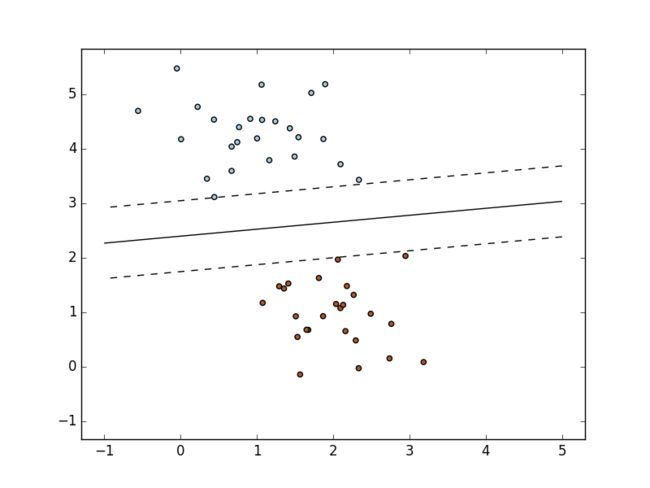
SGD: 最大化边缘以分割超平面,
展示多类SGD在iris数据集的表现
SGD: 权重样本
各种在线求解器的比较
SVM: 为偏斜类分割超平面 (说明部分)

SGDClassifier
支持平均SGD（ASGD）。可以通过设置** average=True **来开启平均化。ASGD的工作原理是通过在每个样本的迭代中，分别平均化其平面SGD的系数。当使用ASGD时，学习率可能会变得很大（耗时下降），甚至会不断地导致一些数据集在训练的耗时减少。

对于使用** logistic 代价函数的分类，另一种 SGD **的变体是在随机平均梯度（SAG）算法中启用平均化策略，其包含在 LogisticRegression
中，同样可以作为一个求解器使用。

1.5.2. 回归#

SGDRegressor
类实现了一个常规的朴素梯度下降学习，其支持对拟合线性模型设置许多不同的代价函数和惩罚项。SGDRegressor
是一个适合用来对有大量训练样本（> 10,000）回归问题，若是对其他回归问题，则建议使用Ridge
，Lasso
，或 ElasticNet
。

可以通过** loss **参数来选择具体是要使用哪个代价函数。SGDRegressor
支持以下几种代价函数：

loss="squared_loss"：最小二乘法。
loss="huber"：稳健回归中的Huber损失。
loss="epsilon_insensitive"：线性支持向量回归。

**huber 和 epsilon_insensitive 代价函数都是能够在稳健回归中使用的。不敏感区的宽度只能通过 epsilon **参数来设置，并且这个参数取决于目标变量的规模。

SGDRegressor
类似 SGDClassifier
，都是支持平均 SGD的。

对带有平方损失和L2惩罚项的回归来说，另一种SGD的可选方案是使用随机平均梯度（SAG）算法，其包含在 Ridge
，同样能够单独作为求解器来使用。

1.5.3. 对稀疏数据使用随机梯度下降#

注意：因为在截距上收缩了学习速率，所以稀疏实现与密集实现的结果会有所不同。

对符合格式要求的任意稀疏矩阵都在 scipy.sparse 中存在内置支持。但是如果要追求最大效率的话，可以使用 scipy.sparse.csr_matrix 内所定义CSR矩阵格式。

示例

使用稀疏特征的文档分类

1.5.4. 复杂度#

SGD的主要优点就在于其执行效率，根据训练样本的数量基本上是呈线性的。如果** X 是一个尺寸为 (n, p) 的矩阵，根据代价函数 O(k·n·p) 进行训练，其中 k 是迭代数量，而 p **则是每个样本非零属性的平均值。

但是近期的研究结果显示，获得期望的最优准确度所需的时间并不是随着训练集大小的增加而增加。

1.5.5. 实用技巧#

SGD对特征缩放很敏感，所以在这里高度建议对数据进行缩放。举例来说，对输入向量** X 的每个特征缩放为值域是[0, 1]或[-1, +1]，又或者是将其标准化为均值为0，方差为1的值域。当然也要对测试集做相同的缩放操作。
这些操作可以使用 StandardScaler **来简单的完成：

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)  # Don't cheat - fit only on training data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)  # apply same transformation to test data

如果你的参数存在内在尺度（例如单词出现频率或指标特征），那么就不应该对其进行缩放。

使用** GridSearchCV 来寻找一个合理的 α 项，通常限制的范围是 10.0**-np.arrage(1, 7)**。
通常来说，当我们观察了大约的训练结果后（观察学习曲线或模型图）就会认为SGD已经收敛了。
以数量为10^6的训练样本为例，鉴于此一个对迭代数量的初步合理的猜想是** n_iter = np.ceil(10**6 / n) ，其中 n **是训练集的数量。
如果你讲SGD应用在使用PCA提取出的特征上，一般的建议是通过寻找某个常数** c **来缩放特征，使得训练数据的平均L2范数等于1。
平均SGD（ASGD）最适合应用在有超大数量的特征与很高的** eta0 **的样本上。

引用

“Efficient BackProp” Y. LeCun, L. Bottou, G. Orr, K. Müller - In Neural Networks: Tricks of the Trade 1998.

1.5.6. 数学公式#

给定一个训练集（x1, y1）,...,（xn, yn），其中** xi ∈ R^n ， yi ∈ {-1, 1} 。我们的目标是在使用模型参数 ω ∈ R^m 和截距 b ∈ R 的情况下，学习线性评分函数 f(x) = ω^T·x + b 。为了做出预测，我们简单的将这个函数用 f(x) 来代替。然后通常是使用最小化正规训练误差来找到适合的模型参数（ω 和 b**）。

最小化代价函数

其中** L 是测量模型（mis）拟合用的代价函数， R 是惩罚模型复杂性的正则化项（也成为惩罚项）。α ＞ 0 **是一个非负超参数。

对不同的分类使用不同的** L **，例如：

Hinge：(软边界) 支持向量机。
Log：Logistic回归。
Least-Squares：岭回归。
Epsilon-Insensitive：(软边界)支持向量回归。

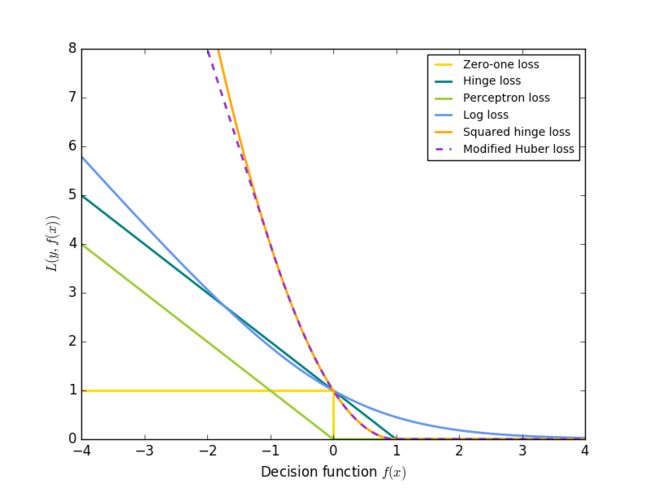
上述的损失函数都可以被认为是误分类误差（0-1）的上限，即下图所示：

损失函数图

常用的正则项** R **有：

L2范数
L1范数，产生稀疏结果
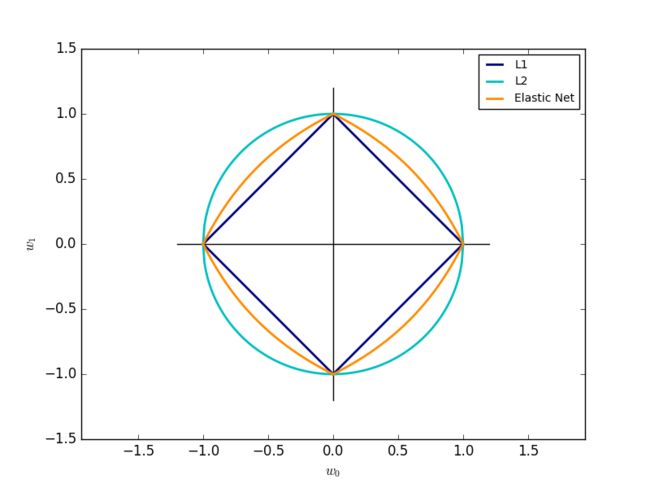
弹性网络，L2与L1的凸组合，其中** p **由** 1 - l1_ratio **得出

下面的图显示了在** R(ω) = 1 **的情况下，使用各种正规化后函数的轮廓：

三种正规化的轮廓

1.5.6.1. SGD##

随机梯度下降是无约束最优化问题的一种优化方式。比较与（批）梯度下降，SGD的方式是分别考虑单个样本来逼近** E(ω， b) **的真实梯度。

SGDClassifier
实现了一个一阶SGD学习。这个算法迭代训练样本并对每一个样本根据下面的公式来更新模型参数：

ω参数

其中** n 是控制着步进的学习速率。截距 b **也是以类似的方式更新，除了不需要正则化。

学习速率** n 可以是一个恒定值或是衰减值。对分类问题而言，默认的学习速率（learning_rate='optimal'**）是通过下面的公式给出：

分类的学习速率公式

上式的** t 是间隔时间（此处是 n_samples * n_iter 的总和），而t0是基于Léon Bottou提出的启发式来确定的，默认是跟权重的初始值一致（这是在假设训练样本的范数是近似为1的情况下）。关于这个的确切定义可以在 BaseSGD 的 _init_t **中找到。

对回归问题而言，默认的学习速率（learning_rate='invscaling'）是通过下面的公式给出：

回归的学习速率公式

其中** eta0 和 power_t 是通过用户在 eta0 和 power_t **输入的超参数。

如果要使用恒定的学习速率则设置** learning_rate='constant' ，固定值则是设置 eta0 **了。

可以通过** coef_ 和 intercept_ **来访问模型参数：

coef_成员保存着权重** ω **。
intercept_成员保存着** b **。

引用

“Solving large scale linear prediction problems using stochastic gradient descent algorithms” T. Zhang - In Proceedings of ICML ‘04.
“Regularization and variable selection via the elastic net” H. Zou, T. Hastie - Journal of the Royal Statistical Society Series B, 67 (2), 301-320.
“Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent”Xu, Wei

1.5.7. 实现细节#

SGD的实现受Léon Bottou的随机梯度SVM 影响。与SvmSGD相似，权重向量代表着标量和向量的乘积，而这允许在L2正则化下能够有效地对权重进行更新。在稀疏特征向量的情况下，截距是参照更小的学习速率（更新频率为学习速率乘以0.01）来更新的，而这说明了会很频繁的对截距进行更新。训练样本被顺序挑出，并且在"观察"每个样本后就将降低学习速率。在该类中我们是采用了Shalev-Shwartz 等人在2007年所提出的学习速率。对于多类分类问题则是采用了"一对多"。然后再正则化方面则是采用了由 Tsuruoka 等人在2009年提出的裁断梯度算法来为L1正则化（弹性网络也包括在内）。最后则是使用了Cython来进行代码实现。

引用

“Stochastic Gradient Descent” L. Bottou - Website, 2010.
“The Tradeoffs of Large Scale Machine Learning” L. Bottou - Website, 2011.
“Pegasos: Primal estimated sub-gradient solver for svm” S. Shalev-Shwartz, Y. Singer, N. Srebro - In Proceedings of ICML ‘07.
“Stochastic gradient descent training for l1-regularized log-linear models with cumulative penalty” Y. Tsuruoka, J. Tsujii, S. Ananiadou - In Proceedings of the AFNLP/ACL ‘09.

（在尝试翻译这篇文档的时候难免会因为各种问题而出现错翻，如果发现的话，烦请指出，谢谢> <）

sklearn文档 — 1.5. 随机梯度下降