计算二进制形式中1的数量这种问题,在各种刷题网站上比较常见,以往都是选择最笨的遍历方法“蒙混”过关。在了解Redis的过程中接触到了variable precision SWAR算法(以下简称VP-SWAR算法),算法异常简洁,是目前已知的同类方法中最快的。但如果对于位运算不是很熟悉的话,却不一定容易理解,所以有必要记录一下。
下面先看看VP-SWAR算法的完整实现,然后再逐行解释。
public int vpSWAR(int i){ i = (i & 0x55555555) + ((i>>1) & 0x55555555); i = (i & 0x33333333) + ((i>>2) & 0x33333333); i = (i & 0x0F0F0F0F) + ((i>>4) & 0x0F0F0F0F); i = (i * 0x01010101) >> 24; return i; }
VP-SWAR算法分为四步,第一步
i = (i & 0x55555555) + ((i>>1) & 0x55555555);
第一步的作用是计算每两位为一组的二进制形式包含1的个数。要理解这句话,我们需要从二进制的角度看看到底发生了什么。首先, 0x55555555 的二进制表示为 0101 0101 0101 0101 0101 0101 0101 0101 ,这个数字的规律是基数位为1,偶数位为0。为简单起见,我们只考虑两位,总共有四种情况,即:
| i | x | i & x 结果 |
| 00 | 01 | 00 |
| 01 | 01 | 01 |
| 10 | 01 | 00 |
| 11 | 01 | 01 |
这里用x代表0b01(0b表示二进制)观察发现, i & (0b01) 是i的基数位对应x的1位,i的偶数位对应着x的0位, i & (0b01) 的结果会将i的偶数位置为0,而基数位保持不变,得到的结果就是i的基数位包含1的个数。 (i >> 1) & 0x55555555 先将i右移一位,也就是将i的基数位对应x的0位,i的偶数位对应着x的1位,然后再与 0x55555555 按位与,计算出来的是i的偶数位包含1的个数。两个计算结果相加就得到i每两位为一组中包含的1的数量,我们最后需要的就是这每两位一组的和。
第二步是在第一步的基础上,计算每四位为一组包含1的个数。按照每2位为一组分组用到了 0x55555555 这个数,那么自然的,按照每4位为一组分组自然就需要 0b0011 这种形式,这就是使用 0x33333333 的原因。理论上, i & (0b0011) 总共有16种情况,但是四位二进制位最多包含4个1,用二进制表示为 0b0100 ,所以经过第一步之后,i最多有5种取值,如下:
| i | x | i & x 结果 |
| 0000 | 0011 | 0000 |
| 0001 | 0011 | 0001 |
| 0010 | 0011 | 0010 |
| 0011 | 0011 | 0011 |
| 0100 | 0011 | 0000 |
观察发现, i & (0b0011) 得到的是i的低两位包含1的个数, (i >> 2) & 0b0011)得到的是i的高两位包含的1的个数,两个结果相加得到每四位包含的1的个数。注意,这里并不是说任何数与 0b0011 按位与得到的都是低两位包含的1的个数,这里的前提是第一步的计算,因为经过第一步计算之后,每两位包含多少个1已经记录了下来,再和 0b0011 按位与才得到正确的结果。例如, 0x0010 & 0x 0011=0x0010 ,但是我们不能说 0x0010 包含两个1,但是如果 0x0010 是经过第一步的计算得来,那才说明 0x0010 记录原始数据低两位有两个1。
第三步在第二步基础上,计算每8位有多少个1,由 0x01 和 0x0011 ,很自然想到 0x00001111 ,其对应的32位的十六进制数就是 0x0F0F0F0F 。
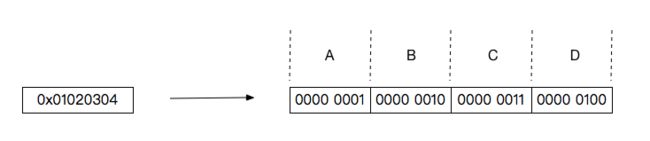
第四步就很有意思了,它不再是计算每16位包含1的个数,而是直接计算32位包含1的个数。对于32位的数来说,可以将其按每8位一组分为4组,分别用ABCD表示,例如 0x01020304 用这种形式表示为:
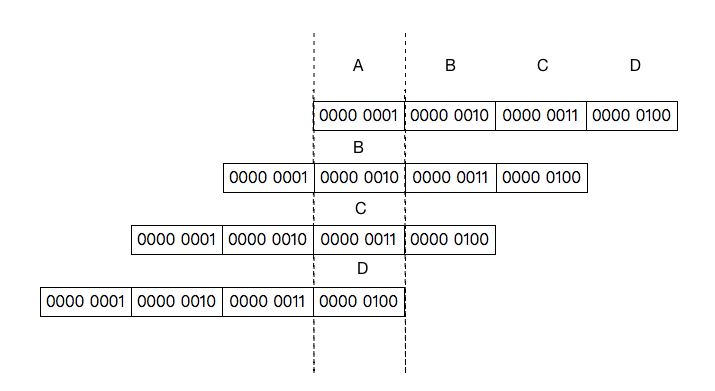
假设 0x01020304 是经过前三步计算之后得到的结果,那么要计算其总共包含多少个1,只需计算A+B+C+D。而ABCD表示的是不同的位区间范围,不能直接相加,该如何快速计算A+B+C+D的值呢?这里又用到了移位运算,将B、C、D分别左移8位、16位、24位,使其分别与A对齐:
我们发现,将数字i分别左移0位、8位、16位、24位然后相加的结果,就是 i * 0x01010101 ,因为 i + (i << 8) + (i << 16) + (i << 24) = i * (1 + 1 << 8 + 1 << 16 + 1 << 24) = i * 0x01010101 。对于32位数字来说,左移之后超过32位的部分会被舍弃,低位补0,将左移之后得到的四个数字相加,结果的高8位的值就是原32位数包含的1的个数,要得到这个值,只需要将结果右移24位,将值放在低8位即可。
到这里,整个算法就结束了,右移的结果就是1的数量。在Redis中,BITCOUNT命令同时使用了查表法和VP-SWAR这两种方法。当要计算的位数小于128位时,使用查表法,否则使用VP-SWAR算法。其中查表法的做法是,程序先存一个256长度的表,按顺序记录从0-255(即 0b00000000 - 0b11111111) 数中二进制1的个数,然后对于输入参数每8位查一次表。