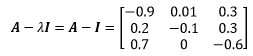线性代数笔记25——马尔可夫矩阵

A^T的特征值

　　矩阵A的特征值和A^T的特征值是一样的。

　　求解特征值的方法是det(A-λI) = 0，根据行列式的性质，矩阵的行列式等于矩阵转置的行列式，因此：

　　因此λ也是A^T的特征值。

马尔可夫矩阵

　　矩阵A有2个特点：A中的所有元素都是非负的；A中的每一列之和都等于1。形如A的矩阵称为马尔可夫矩阵。马尔可夫矩阵主要应用在概率领域。将一个马尔可夫矩阵进行方幂运算仍然得到马尔可夫矩阵。

　　当处理一个微分方程时，特征值0意味着得到了一个稳态。当进行矩阵的方幂运算时，稳态的条件包括：

1. λ₁=1是特征值之一。
2. 其他特征值的绝对值比1小，|λ_i|<1

　　给定一个向量u₀和一个能够对角化的矩阵A，如果u_k+1=Au_k，那么：

　　当λ₁=1，其他特征值的绝对值比1小时，则u_k在k增大的过程中趋近于C₁x₁，即给出了一个稳态。x₁是A的特征向量，它的每个分量都是大于或等于0的值。

为什么一定有λ=1的特征值

　　马尔可夫矩阵的每一列之和为1，这个性质保证了矩阵有一个λ=1的特征值。

　　回顾前面的章节，我们通过下式来计算A的特征值：

　　如果λ=1时是一个特征值，那么A-λI一定是一个奇异矩阵：

　　A减去单位向量相当于把A的每一列之和减去1，此时所有行向量相加得到0向量，这意味着一个行向量可以用另外两个行向量表示，因此行向量是线性相关的，A-I是奇异矩阵，一定会有det(A-I)=0。

人口的流动

　　对于方程u_k+1=Au_k，A是马尔可夫矩阵，我们用人口的流动解释马尔可夫矩阵。

　　u的分量分别表示两个城市人口，A中的每一列代表人口的去留比例。第一列的0.9表示留在u_A的人口占u_A总人口的90%，剩余10%流入u_B；第二列的0.2表示从u_B流入u_A的人口占u_B的20%，剩余80%留在u_B。每一列的加和为1保证了总人口不变。如果有一个初始值：

　　表示在t=0时刻，u_A的总人口是0，是个待开辟的新城市，u_B有1000人。经过一次迁徙，在t=1时刻：

 

　　这次迁徙主要是从u_B迁入u_A，有200人进入u_A，剩余800人留在u_B。

 

　　我们希望获得长时间迁徙后的人口分布，这需要知道A的特征值和特征向量。A是马尔可夫矩阵，因此一个特征值是λ₁=1，通过矩阵的迹可知另一个特征值是λ₂=0.9+0.8-1=0.7。由此可以求得两个特征向量：

　　由于两个特征值符合方幂运算时达到稳态的条件，所以u_k在k增大的过程中趋近于C₁x₁，即最后经过多年的迁徙，两个城市的人口趋近于定值：

　　

综合示例

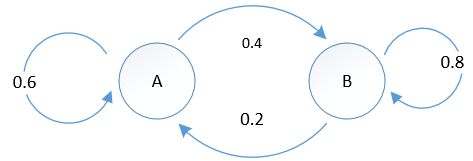
　　一个颗粒可以在A和B之中来回跳动，跳动的概率如下图所示：

　　如果颗粒在A，下一次跳到B的概率是0.4，仍然留在A的概率是0.6；如果在B，下一次跳到A的概率是0.2，仍然留在B的概率是0.8。

　　如果颗粒最初在A，那么它一步之后，n步之后，无穷步后留在A或移动到B的概率是多少？

　　

　　首先构建模型，将上图构造成马尔可夫矩阵：

　　第一列表示颗粒停留在A的概率是60%，从A跳到B的概率是40%；第二列表示从B跳到A的概率是20%，停留在B的概率是80%。

　　颗粒最初在A位置，因此初始条件是：

　　第一次移动后，停留在A的概率是60%，移动到B的概率是40%：

　　第n次移动后：

　　u_n的两个分量分别表示第n次移动后停留在A的概率和移动到B的概率。

　　无穷步后，留在A的概率是33.33%。

　　

---

　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注作者公众号“我是8位的”