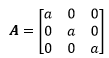原文 | https://mp.weixin.qq.com/s/zdQttJfuubyztiVplScbwA
对称矩阵
对称矩阵是最重要的矩阵之一,对于对称矩阵来说,A=AT。矩阵的特殊性也表现在特征值和特征向量上,比如马尔可夫矩阵的有一个值为1的特征值,对称矩阵的特征值又有哪些特性呢?
本文的相关知识:
正交向量和正交矩阵 (线性代数20——格拉姆-施密特正交化)
投影矩阵 (线性代数18——投影矩阵和最小二乘)
复数 (闲话复数(1))
谱定理
对于实对称矩阵来说,它的特征值也为实数,并且能够挑选出完全正交的特征向量。
单位矩阵是对称矩阵,它的特征值都是1,并且单位矩阵的每一个列向量都是特征向量,它们完全正交,因此单位矩阵肯定符合实对称矩阵特征值和特征向量的性质。
P是投影矩阵也是单位矩阵,x是一个二维向量,如果x在平面的投影是x本身,即Px=x,那么平面内的所有向量都是P的特征向量。更一般的情况是,在重特征值的情况下,可能一个平面内的所有向量都能作为特征向量,因此我们说实对称矩阵“能够挑选出完全正交的特征向量”,下面是一个例子:
A的特征值全部是λ=a,对于任何向量都有Ax=λx,因此任何向量都是特征向量,但这些特征向量并不都是正交的,所以是从中选出一套正交向量。
如果A有n个线性无关的特征向量,那么A可以对角化为A=S∧S-1,如果A是对称矩阵,那么A对角化后有更好的性质:
![]()
Q是A的特征向量矩阵,同时也是正交矩阵,列向量是标准正交基。对于一个列向量标准正交的矩阵来说,矩阵的逆等于矩阵的转置,因此:
![]()
上式是说,如果给定一个对称矩阵,那么这个矩阵就可以分解成正交矩阵乘以特征值矩阵再乘以正交矩阵的转置的形式,这种分解在数学上称为“谱定理”,将特征值的集合视为谱,力学上称为“主轴定理”。
谱定理展示了对称矩阵的对称性,Q∧QT的转置还是原矩阵:
![]()
∧是对角矩阵,它的转置还是∧。
为什么是实特征值?
矩阵的特征值可能为虚数,但实对称矩阵的特征值一定是实数,这又是什么原理?
先解释一下共轭复数(conjugate complex number):两个实部相等,虚部互为相反数的复数互为共轭复数。当虚部不为零时,共轭复数就是实部相等,虚部相反;如果虚部为零,其共轭复数就是自身。复数z的共轭复数用z上面加一横表示。
“轭”的本意是两头牛背上的架子,轭使两头牛同步行走。共轭是指按一定的规律相配的一对。
如果实矩阵A有特征值λ和特征向量x,则Ax=λx。如果λ是复数,则λ的共轭复数满足:
![]()
如果等号两侧同时转置:
λ是对角矩阵,其共轭仍然是对角矩阵,因此:
![]()
两侧同时乘以x:
![]()
另一方面,将Ax=λx两侧同时乘以x共轭的转置:
![]()
现在假设A是对称矩阵,则①和②相等,即:
根据共轭复数的定义,如果一个复数的共轭等于这个数本身,那么其虚部为0,即这个数是实数。
现在的问题是如何证明![]() ?
?
对于虚数来说,i2=-1,(bi)2=-b2。对于复数来说,z=a+bi来说,它的模几何意义是复平面上一点(a,b)到原点的距离,模长的计算公式是:
![]()
因此:
对于复矩阵来说,若A是共轭对称复矩阵,即![]() ,那么上面的推导仍然成立,A的特征值也是实数。
,那么上面的推导仍然成立,A的特征值也是实数。
朝向正交向量的投影矩阵
对于一个实对称矩阵A=AT,可以写成下面的形式:
根据投影矩阵的定义:向量b的在向量a上的投影是一个矩阵作用在b上得到的,这个矩阵就叫做投影矩阵(Projection Matrix),用大写的P表达:
由于Q中的向量是正交向量,因此:
所以qkqkT是某个向量在qk上的投影矩阵,因此每一个对称矩阵也是朝向正交向量的投影矩阵的线性组合。
特征值的符号
我们已经知道对称矩阵的特征值是实数,下一个问题是弄清它们的符号,这对微分方程来说意味着状态是否稳定。
我们可以通过计算的方式求解特征值,然后回答特征值的符号问题,但对于一个大型矩阵来说,通过计算det(A-λI) = 0来求解特征值并不容易。值得庆幸的是,对于对称矩阵来说,主元和特征值存在着相关性:主元和特征值的个数一样,且正负主元的个数都和正负特征值的个数相同。
正定矩阵
正定矩阵是一类特殊的实对称矩阵,如果一个矩阵M满足对于任何非零向量z,都有zTMz> 0,那么这个矩阵是正定矩阵。
正定矩阵有很多重要的性质,其中一个是:正定矩阵的特征值和主元都是正数。
来看一个正定矩阵:
首先A是一个对称矩阵,现在来计算一下它的主元。可以通过化简行阶梯矩阵的形式求得主元,在经过变换后,矩阵表示的“数表”改变了,但是如果将矩阵看方程组,那么方程组的本质没有变,可以将初等变换看成方程组的消元过程。
两个主元是5和11/5。另一种方式或许更为简单,原矩阵中转换成上三角矩阵的时候,一定能变成下面的形式:
它的行列式是主对角线元素的乘积,行列式的值又和原矩阵的行列式相等,因此a=det(A)/5=11/5。
类似地,可对角化的矩阵可也以化成对角元素都是其特征值的对角矩阵,而行列式的值不变,对角矩阵的行列式就是对角元素相乘,因此A的行列式也等于A的特征值的乘积。
特征值:
与行列式的关系
正定矩阵的主元和特征值都是正数,因此可以确定其行列式也是正数(行列式等于主元的乘积,也等于所有特征值的乘积),但行列式是正数的矩阵不一定是正定矩阵,比如下面这个矩阵,虽然行列式是正值,但并不是一个正定矩阵,甚至都不是对称矩阵:
如果把行列式作为正定矩阵的判定依据,则对于n阶矩阵来说,需要矩阵左上角的所有k×k (1≤k≤n)子行列式均为正,才能判定矩阵是正定矩阵。
正定矩阵的性质
正定矩阵都是可逆的。
矩阵可逆的条件是行列式不等于0,行列式等于特征值的乘积,正定矩阵的性质又规定特征值是正数,因此正定矩阵的行列式一定大于0,是可逆矩阵。
只有正定的投影矩阵才是单位矩阵。
如果P是投影矩阵,那么P的特征值要么是0,要么是1。如果P是正定的,那么根据定义,它的特征值只能是1,特征值矩阵是单位矩阵,因此:
![]()
如果D是一个对角元素都是正数的对角矩阵,那么D一定是个正定矩阵。
对角矩阵肯定是对称的,对于任何非零向量x来说:
满足正定矩阵的定义。
若A是正定矩阵,则A的逆矩阵也是正定矩阵。
首先证明矩阵A的逆是对称矩阵。因为A是正定的,所以:
再证明xTA-1x > 0
A是正定矩阵,对于任意向量u来说,uTAu > 0,因此xTA-1x > 0,A-1也是正定矩阵。
两个正定矩阵的和是正定矩阵。
正实数与正定矩阵的乘积是正定矩阵。
作者:我是8位的
出处:https://mp.weixin.qq.com/s/zdQttJfuubyztiVplScbwA
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”