Erlang学习：快速排序和尾递归

上一篇博客介绍了尾递归，是我自己的理解，从编译器的角度考虑的，在看算法导论的时候发现了下面这个题目，里边模拟了尾递归，看看是怎么模拟尾递归的。先用Python实现下面的算法，然后用Erlang实现。

算法导论中的题目：

The QUICKSORT algorithm of Section 7.1 contains two recursive calls to itself. After the call to PARTITION, the left subarray is recursively sorted and then the right subarray is recursively sorted. The second recursive call in QUICKSORT is not really necessary; it can be avoided by using an iterative control structure. This technique, called tail recursion, is provided automatically by good compilers. Consider the following version of quicksort, which simulates tail recursion.

QUICKSORT'(A, p, r)
1 while p < r
2 do ? Partition and sort left subarray.
3 q ← PARTITION(A, p, r)
4 QUICKSORT'(A, p, q - 1)
5 p ← q + 1

1.Argue that QUICKSORT'(A, 1, length[A]) correctly sorts the array A.

Compilers usually execute recursive procedures by using a stack that contains pertinent information, including the parameter values, for each recursive call. The information for the most recent call is at the top of the stack, and the information for the initial call is at the bottom. When a procedure is invoked, its information is pushed onto the stack; when it terminates, its information is popped. Since we assume that array parameters are represented by pointers, the information for each procedure call on the stack requires O(1) stack space. The stack depth is the maximum amount of stack space used at any time during a computation.

2.Describe a scenario in which the stack depth of QUICKSORT' is Θ(n) on an n-element input array.

3.Modify the code for QUICKSORT' so that the worst-case stack depth is Θ(lg n). Maintain the O(n lg n) expected running time of the algorithm.

1.其实QUICKSORT'和QUICKSORT做的partition都是一样的。

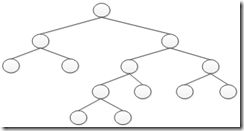
QUICKSORT'先做一个Partition，找到q，然后对左边的子序列排序，接着并不是对右边的子序列排序，而是先将子序列进行一次Partition。本质上是一样的。 两者有什么区别呢？那就是递归的调用顺序 QUICKSORT的调用树是一个二叉树。一个QUICKSORT仅调用两次自己。而QUICKSORT'可以调用多次自己，这样它的调用树就不是二叉了。

QUICKSORT的递归树

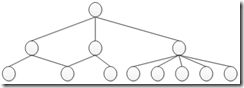
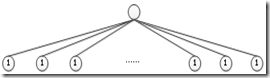
QUICKSORT'的递归树

注意题目中说到了simulate tail recursion，而不是真正的tail recursion，是怎么实现的呢？如果一颗树的度变大了，那么它的高度自然就变小了。所以说为了达到尾递归的效果，可以在递归过程中，让递归函数尽量多的调用自己。

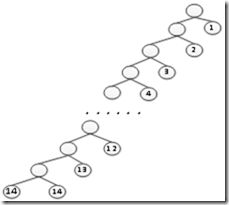
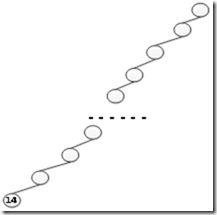
2.栈深度就是递归树的深度，如果栈的深度是 Θ(n)，那么这棵树必须是一条直线。这样Partition每次返回的q必须等于r或者p。一个所有元素都相等的序列就满足这个条件。或者一个排好序的序列，也满足这个条件。这种情况下，QUICKSORT'每次只调用了一次自己。

3.栈深度跟序列长度是有关系的，最大的情况也就是栈长度。如果我们让QUICKSORT的参数长度尽量小，那么栈深度就不会太大了。怎么做呢？

上面我们说了，先Partition一次，然后左边的递归调用QUICKSORT，右边的先Partition一次再递归。可以这样，Partition之后，选一个短的进行QUICKSORT，然后再将产生的长序列Partition，这样QUICKSORT的序列长度最大不会超过n/2，栈深度也就不会超过n/2了。运行时间是不变的。

这个有点平衡树的思想了。QUICKSORT'调用树的度数是不定的，有可能是一条直线，我们要尽量让这棵树平衡。

QUICKSORT'(A, p, r)
1 while p < r
2 do
3      q ← PARTITION(A, p, r)
4      if q - p <= r - q
5         then QUICKSORT'(A, p, q - 1)
6              p ← q + 1
7     else
          then QUICKSORT'(A,p+1,r)
               r = q - 1

使用Python实现

我们先用Python来实现上述各种算法，看看是不是真正减少了栈深度。

def Partition(A,p,r):
    if p < r:
        i = p - 1
        j = p
        while j < r:
            if A[j] <= A[r]:
                i = i + 1
                tmp = A[j]
                A[j] = A[i]
                A[i] = tmp
            j = j + 1
        tmp = A[r]
        A[r] = A[i+1]
        A[i+1] = tmp
        return i + 1

def qsort1(A,p,r,depth):
    if p >= r:
        print "Recursion Depth:",depth
    if p < r:
        q = Partition(A,p,r)
        qsort1(A,p,q-1,depth+1)
        qsort1(A,q+1,r,depth+1)
def qsort2(A,p,r,depth):
    if p >= r:
        print "Recursion Depth:",depth
    while p < r:
        q = Partition(A,p,r)
        qsort2(A,p,q-1,depth+1)
        p = q + 1
def qsort3(A,p,r,depth):
    if p >= r:
        print "Recursion Depth:",depth
    while p < r:
        q = Partition(A,p,r)
        if q - p < r - q:
            qsort3(A,p,q-1,depth+1)
            p = q + 1
        else:
            qsort3(A,q+1,r,depth+1)
            r = q - 1


A=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
qsort1(A,0,len(A)-1,0)
print A
qsort2(A,0,len(A)-1,0)
print A
qsort3(A,0,len(A)-1,0)
print A

B=[3,2,6,5,7,8,3,9,2,5,4,1,5,3,2]
qsort1(B,0,len(B)-1,0)
print B

B=[3,2,6,5,7,8,3,9,2,5,4,1,5,3,2]
qsort2(B,0,len(B)-1,0)
print B

B=[3,2,6,5,7,8,3,9,2,5,4,1,5,3,2]
qsort3(B,0,len(B)-1,0)
print B

运行结果：

Recursion Depth: 14
Recursion Depth: 14
Recursion Depth: 13
Recursion Depth: 12
Recursion Depth: 11
Recursion Depth: 10
Recursion Depth: 9
Recursion Depth: 8
Recursion Depth: 7
Recursion Depth: 6
Recursion Depth: 5
Recursion Depth: 4
Recursion Depth: 3
Recursion Depth: 2
Recursion Depth: 1
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Recursion Depth: 14
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
Recursion Depth: 1
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Recursion Depth: 2
Recursion Depth: 3
Recursion Depth: 3
Recursion Depth: 4
Recursion Depth: 4
Recursion Depth: 5
Recursion Depth: 5
Recursion Depth: 4
Recursion Depth: 4
Recursion Depth: 4
Recursion Depth: 3
[1, 2, 2, 2, 3, 3, 3, 4, 5, 5, 5, 6, 7, 8, 9]
Recursion Depth: 2
Recursion Depth: 2
Recursion Depth: 3
Recursion Depth: 3
Recursion Depth: 2
[1, 2, 2, 2, 3, 3, 3, 4, 5, 5, 5, 6, 7, 8, 9]
Recursion Depth: 2
Recursion Depth: 2
Recursion Depth: 2
Recursion Depth: 2
Recursion Depth: 2
Recursion Depth: 1
Recursion Depth: 1
[1, 2, 2, 2, 3, 3, 3, 4, 5, 5, 5, 6, 7, 8, 9]

打印一次Depth，说明这是递归树的一个叶子。可以根据这些叶子画出递归树。

我们画出对[1,1,…,1]排序的递归树

qsort1:

qsort2:

qsort3:

 

 使用Erlang实现

快速排序是一种原地排序(in-place sort)，需要交换元素，但是Erlang中变量不允许修改，那么就没法实现原地排序。Erlang中如何实现快速排序呢？

预备知识：

     1.Erlang的列表

     [1,2,3]

     [1,a,'hello world',[]]

    2. 列表基本操作

       长度 length([1,2,3]) = 3 ，length([[],[]]) = 2

      列表的头 hd([a,b,c,d]) = a ，hd([1]) = 1。hd([])是不对的，会出现运行时错误。

      列表的尾 tl([a,b,c,d]) = [b,c,d]，tl([1]) = []。 tl([])也会出现运行时错误。

      Erlang的列表推断：[Expr || Qualifier1,...,QualifierN]

                   Expr可以是任意的表达式，而Qualifier是generator或者filter。还是各举例子说明下。

                   [X||X<-[1,2,3,4,5,6], X<5]

                   [X||X<5, X<-[1,2,3,4,5,6]] 错，从左向右依次寻找减少范围，X<5没有范围

                   [X||X>1,X<5] 错，未在列表上操作

                   [X*2|| X<-[1,2,3]]

                   [X+Y||X<-[1,2,3],Y<-[1,2,3],Y>X]

      3.函数的字句之间用“，”分隔，同一个函数的不同逻辑分支用“;”分隔，函数最后用“."结束。

      4.case语句和if语句

case Expr of
     Pattern1 [when Guard1] -> Seq1;
     Pattern2 [when Guard2] -> Seq2;
     ...
     PatternN [when GuardN] -> SeqN
end

    注意：seq内部使用","分隔，而seq之间使用";"分隔，end之前的seq不需要分隔符，end后面是什么视情况而定。保护字句可有可无。

if
 Guard1 -> Sequence1 ;
 Guard2 -> Sequence2 ;
 ...
end

      if语句的分隔符规则和case一样。

下面是Erlang实现的快速排序

-module(qsort).
-export([qsort/1]).

qsort([])->[];
qsort([Pivot|T])->
qsort([X||X<-T,X=<Pivot]) ++ [Pivot] ++ qsort([X||X<-T,X>Pivot]).

Erlang的小于或等于竟然是"=<"，我靠

-module(test1).
-export([test1/1]).

test1(0) -> 0;
test1(n) ->
           test1(n-1).

这段代码一直错，忘了Erlang中变量首字母必须大写。

 

由于上面的Python代码使用了迭代，而在Erlang中是不存在迭代的，因此不能实现和上面相同的算法。但是也可以通过增加函数调用自身的次数减小栈的深度。

-module(qsort).
-export([qsort1/2,qsort2/2]).

qsort1([],Depth)->
    io:format("Recursion Depth: ~.B~n",[Depth]),
    [];
qsort1([Pivot|[]],Depth)->

    io:format("Recursion Depth: ~.B~n",[Depth]),

    [Pivot];

qsort1([Pivot|T],Depth)->
    qsort1([ X || X <- T,X =< Pivot],Depth+1) ++ [Pivot] ++ qsort1([X||X<-T,X>Pivot],Depth+1).

qsort2([],Depth)->
    io:format("Recursion Depth~.B~n",[Depth]),
    [];
qsort2([Pivot|[]],Depth)->
    io:format("Recursion Depth~.B~n",[Depth]),
    [Pivot];

qsort2([Pivot|T],Depth)->
    L = [X || X <- T, X =< Pivot],
    R = [X || X <- T, X > Pivot],
    %io:format("Pivot:~.B~n",[Pivot]),
    %io:format("Left:~w~n",[L]),
    %io:format("Right:~w~n",[R]),
    case length(L) =< length(R) of
       true->
        if
            length(R) > 0 ->
                RL = [X || X <- tl(R),X =< hd(R)],
                RR = [X || X <- tl(R),X > hd(R)],
                qsort2(L,Depth+1) ++ [Pivot] ++ qsort2(RL,Depth+1) ++ [hd(R)] ++ qsort2(RR,Depth+1);
            length(R) == 0 ->
                qsort2(L,Depth+1) ++ [Pivot] ++ qsort2([],Depth+1)
        end;
       false->
        if
            length(L) > 0 ->
                LL = [X || X <- tl(L),X =< hd(L)],
                LR = [X || X <- tl(L),X > hd(L)],
    %io:format("xPivot:~.B~n",[hd(L)]),
    %io:format("xLeft:~w~n",[LL]),
    %io:format("xRight:~w~n",[LR]),
                qsort2(LL,Depth+1) ++ [hd(L)] ++ qsort2(LR,Depth+1) ++ [Pivot] ++ qsort2(R,Depth+1);
            length(L) == 0 ->
                qsort2([],Depth+1) ++ [Pivot] ++ qsort2(R,Depth+1)
        end
    end.

运行结果

Eshell V5.8.5  (abort with ^G)
1> qsort:qsort1([1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],0).
Recursion Depth: 14
Recursion Depth: 14
Recursion Depth: 13
Recursion Depth: 12
Recursion Depth: 11
Recursion Depth: 10
Recursion Depth: 9
Recursion Depth: 8
Recursion Depth: 7
Recursion Depth: 6
Recursion Depth: 5
Recursion Depth: 4
Recursion Depth: 3
Recursion Depth: 2
Recursion Depth: 1
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
2> qsort:qsort2([1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],0).
Recursion Depth7
Recursion Depth7
Recursion Depth7
Recursion Depth6
Recursion Depth6
Recursion Depth5
Recursion Depth5
Recursion Depth4
Recursion Depth4
Recursion Depth3
Recursion Depth3
Recursion Depth2
Recursion Depth2
Recursion Depth1
Recursion Depth1
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
3> qsort:qsort1([3,2,6,5,7,8,3,9,2,5,4,1,5,3,2],0).
Recursion Depth: 4
Recursion Depth: 4
Recursion Depth: 3
Recursion Depth: 3
Recursion Depth: 3
Recursion Depth: 5
Recursion Depth: 5
Recursion Depth: 4
Recursion Depth: 3
Recursion Depth: 3
Recursion Depth: 4
Recursion Depth: 4
[1,2,2,2,3,3,3,4,5,5,5,6,7,8,9]
4> qsort:qsort2([3,2,6,5,7,8,3,9,2,5,4,1,5,3,2],0).
Recursion Depth3
Recursion Depth3
Recursion Depth3
Recursion Depth2
Recursion Depth3
Recursion Depth3
Recursion Depth3
Recursion Depth3
Recursion Depth3
Recursion Depth3
Recursion Depth2
Recursion Depth2
Recursion Depth2
Recursion Depth2
Recursion Depth2
[1,2,2,2,3,3,3,4,5,5,5,6,7,8,9]