线性同余生成随机数的一点思考

今天下午 pk 和我讨论了一个问题，他看到在另一个项目组的 lua 代码里有一段使用线性同余产生随机数的代码，但是那个项目组的同事告诉他这个函数生成的随机数是分布不均的。于是他想到了我前两天给他讲的关于 lua 里 % 这个取余数的符号跟 c 语言里的差别。由此展开了讨论。

首先铺陈背景，线性求余生成随机数的方式很普遍，对随机数要求不高的代码都可以使用这种方式，因为它实现简单，如果不知道原理的可以去 goole 一下。关于它所产生的随机数是否在域上分布均匀，暂且不论，权当均匀的吧。

我把代码做了简化，只留下最核心的几行，我们来看一下，这个产生伪随机数的算法是这样的：

local IA = 3877
local IB = 29573

local g_seed = 42

function setseed(seed)
	g_seed = seed
end

function getrandom(max)
	max = max or 100
	g_seed = g_seed * IA + IB
	print(g_seed)
	return g_seed % max
end

还算是简单的线性同余，当然各种边界条件的判断我都省略了。

这段代码的问题在哪里呢？首先有个前提条件，就是在实际我们求随机数的时候，不会去求一个负数域的随机数，换句话说，调用 getrandom() 函数传递的 max 值肯定是大于 0 的。

线性求余的公式倒是很简单：y = kx + b。这里我们的 k = IA = 3877，b = IB = 29573。为什么是这两个数呢，自己 google 吧。

这种方法求随机数，其实就是根据一个 x 值，来计算出 y 值，然后用 y 值模取随机数范围，并把这个 y 值作为下一次调用时的 x 值。举个例子，比如这里最初的 x 值就是那个 g_seed = 42，为什么是 42 也自己 google 吧。然后我要求一个 100 内的随机数，我调用一下 getrandom(100)，计算过程如下：

g_seed = 42 * 3877 + 29573 = 192407

结果为 g_seed % 100 = 7

接着我又调用一次 getrandom(100) 想得到第二个随机数，计算过程就变成：

g_seed = 192407 * 3877 + 29573 = 745991512

结果为 g_seed % 100 = 12

当然我们肯定不会让 g_seed 超过一个 double 能表示的整数范围，额外处理这里就不谈了，这里说明的是工作的原理就是这样。

如果这个原理在 C/C++ 里面是不会有问题的，但是对于 lua 来说，% 号确实放这里不太合适，因为 lua 里 % 操作符等价于： a % b == a - math.floor( a / b ) * b

可以看这里 http://www.lua.org/manual/5.1/manual.html#2.5.1

这样会有什么问题？由于我们一般不会 % 一个负数，因为求随机数范围一般是正数，但是 g_seed 却是可以由用户来设置的，所以我们无法保证 g_seed 始终为正数，根据上面这个等式，如果 a 为负数，b 为正数，那么 lua 里这个 % 的结果就肯定是一个正数。

这一点对我们的线性同余求随机数会造成什么问题呢？

问题就在于它使得随机的分布不在均匀，当然前提是我们假设之前的分布是均匀的。它使得当 g_seed 为负数时，原本应该得到负数随机数结果的那部分值变为了正数，导致随机数分布向一方倾斜。

我们先来看线性同余的一些性质，令最初的 x 为 x[0]：

我们发现线性同余求得的随机数分别是：

x[1] = kx[0] + b

x[2] = k^2x[0] + kb +b

……

r[1] = (kx[0] + b) % max

r[2] = (k^2x[0] + kb +b) % max

r[3] = (k^3x[0] + k^2b + kb + b) % max

……

我们来考虑 x[n]， x[n] = k^nx[0] + b(k^n-1)/(k-1)

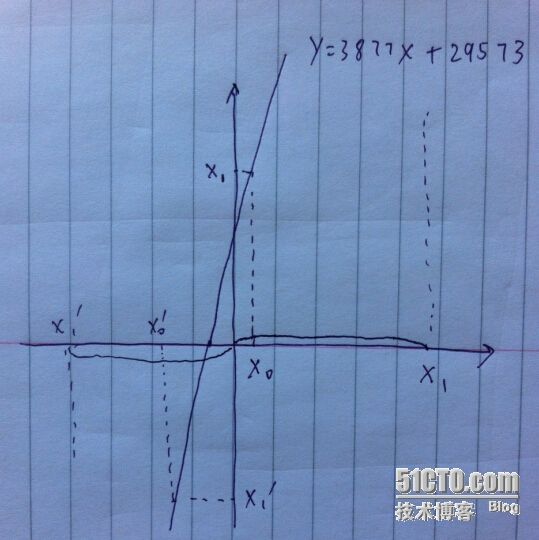
因为我们来看函数 y = 3877x + 29573 的函数图形：

可以看到，如果 x[0] 取一个正数，那么下一个 x[1] 会是一个更大的正数，之后的所有 x 都会更大；如果 x[0] 取一个比较大的负数的时候，之后的 x 都会是更大的负数，那么必然存在一个转折点，x[0] 取这个值的时候，之后的所有 x 都等于 x[0] ，这也就是这个函数的不动点，对于我们这段代码来说，令 3877x + 29573 = x，可以求出 x = - 29573 / 3876，如果 g_seed 最开始取了这个不动点的值，那么这个求随机数的算法就废了，因为每次的随机数都是一样的。

我其实想知道的是，最开始 g_seed 需要取一个怎么样的数，能够保证之后的所有 g_seed 都是单调增加的。当然只有当 g_seed 的取值范围存在负数的时候，我们的随机结果才是分布不均匀的。对这段代码来说，想要分布均匀，只需要最初的 g_seed 为非负数就不会有问题。

我们来寻找更普遍的性质，如果不改变这段代码的写法，依然使用 lua 的这个 % 操作符的含义（a % b == a - math.floor( a / b ) * b）来线性求余数产生伪随机数时，如果要保证随机数分布均匀，那么必须保证 x[n] 恒为非负数（n>=1）。

也就是 x[n] = k^nx[0] + b(k^n-1)/(k-1) 要恒大于等于 0（n>=1） 。k，b，x[0] 均为常数，我们整理得到：

x[n] = (x[0] + b/(k-1))k^n - b/(k-1)

对它求导得到：

x'[n] = (x[0] + b/(k-1))k^nlnk

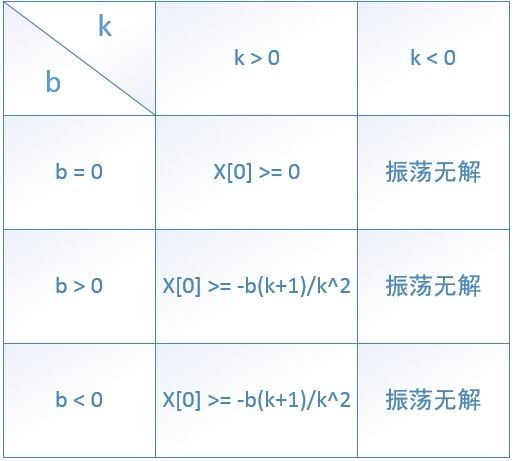
我们想知道当 b 和 k 确定时（k～=0）， x[0] 取什么数时，（1）x[1] >= 0 且 （2）x'[n] > 0。

（1） =》x[0] >= -b/k

（1）带入（2）得到：

并且我们还发现一点，就是当 k  > 1 的时候，x[n] 的绝对值随着 n 的增大是越来越大的，当 0 < k < 1 的时候， x[n] 的绝对值是收敛到 b 的绝对值的。

应用这个表我们最后知道，对于这段代码的 k，b 来说，x[0] 也就是 g_seed 最小不能小于 -29573 × 3878 / 3877^2，差不多是 -7.6 左右，只要最初的 g_seed 比这个值大，那么这段代码求出来的随机数就可以看作是没有问题的。

至此终于知道这段代码风险在哪了，不过既然知道了，就动手改一下呗，可代码是别人的动不得，囧。最近我要离职了，准备找一个新的环境，不知道朋友们有没有觉得靠谱的地，向我推荐下呗：）