今天看了python的教学视频:
https://www.safaribooksonline.com/library/view/python-programming-language/9780134217314/PYMC_08_03.html
讲到了python中多重继承的使用,视频中用多重继承的Mixin+父类实现了装饰者模式。
参考:
https://makina-corpus.com/blog/metier/2014/python-tutorial-understanding-python-mro-class-search-path
分界
python的MRO算法有新旧两种,但并不是以python2和python3为界,具体的分隔为:在python2中如果定义类的时候没有指定父类是object,即定义为
class A:
pass
的使用旧算法。如果指定父类为object的:
class A(object):
pass
使用新算法,python3都是用新算法。
旧算法
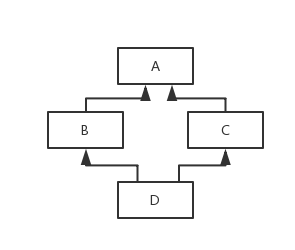
先看示例,类图:
代码:
class A:
def who_am_i(self):
print("I am a A")
class B(A):
def who_am_i(self):
print("I am a B")
class C(A):
def who_am_i(self):
print("I am a C")
class D(B,C):
def who_am_i(self):
print("I am a D")
d1 = D()
d1.who_am_i()
毫无疑问这段代码会输出“I am a D”,稍微改一下D的定义:
class D(B,C):
pass
这时候找到了B实现的方法所以打印出“I am a B”,如果我们把B的实现也去掉:
class B(A):
pass
奇怪的事情发生了,输出是“I am a A”,因为旧算法的MRO推导算法很直观,它使用树状结构组织类。当函数调来到来的时候从左往右的使用深度优先遍历父类:
1,检查对象是否实现了方法
2,如果没有找到,检查首个父类是否实现了该方法
3,如果没有找到,检查本类是否还继承了其他类,是的话从其他分支向上追溯
所以对于本例,查找的顺序就是D B A C A,最后一个A不重复加入最终的顺序是D B C A
来一个例子检查:
class A1():
# def who_am_i(self):
# print("I am a A1")
pass
class A2():
def who_am_i(self):
print("I am a A2")
class A3():
def who_am_i(self):
print("I am a A3")
class B(A1, A2):
# def who_am_i(self):
# print("I am a B")
pass
class C(A3):
def who_am_i(self):
print("I am a C")
class D(B,C):
# def who_am_i(self):
# print("I am a D")
pass
d1 = D()
d1.who_am_i()
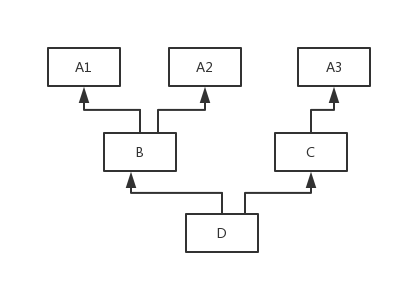
类图为:
套用刚才的规则,查找方法的顺序应该是D B A1 A2 C A3,所以上述代码在python2上的输出是“I am a A2”
新算法
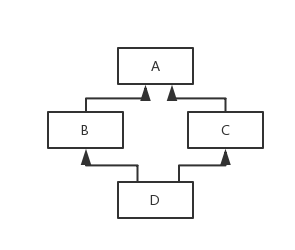
仍然以第一段代码作为例子,重新贴一下类图
新算法在构建MRO的时候第一步与旧算法一样,所以初步结果是D B A C A,然后从左到右判断每个元素是否为“好头(good head)”,不是的话从链中去掉。“好头(good head)”的定义是 - 从该元素开始到链尾,不存在任何元素是该元素的子类 - 初步结果的D, B没问题,第一个A不是好头因为C是其子类所以去掉,再往后的C A也没问题了,最终结果是D B C A,所以在python 3以及当A继承于object的时候如果D,B都不实现who_am_i则最终输出的是“I am a C”。
不可构建的MRO - 新算法补充
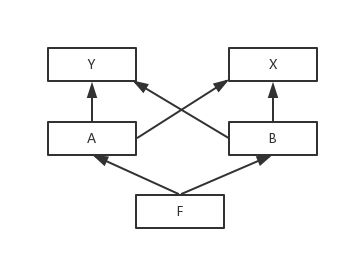
考虑如下蛋疼的继承结构:
代码:
class X():
def who_am_i(self):
print("I am a X")
class Y():
def who_am_i(self):
print("I am a Y")
class A(X, Y):
def who_am_i(self):
print("I am a A")
class B(Y, X):
def who_am_i(self):
print("I am a B")
class F (A, B):
def who_am_i(self):
print("I am a F")
f = F()
f.who_am_i()
如果使用“新算法”,按照上述章节的分析,构建出来的MRO结果应该是F A B Y X,使用python 3跑一遍,结果得到输出:
Traceback (most recent call last):
File "bad_mro.py", line 26, in
class F(A, B):
TypeError: Cannot create a consistent method resolution
order (MRO) for bases X, Y
这又是啥毛病呢,实际上新算法用的是线性算法记为L[]运算以及merge()操作来构造MRO,改线性算法描述为:类C的线性结果是C与merge(C的所有父类的线性结果)之和,用表达式表示为:
L[C(B1...Bn)] = C + merge(L[B1]...L[Bn], B1...Bn)
上边例子的表达式就是:
L[F(A, B)] = F + merge(L[A], L[B], A, B)
merge()运算的规则是:
1,取出merge()中第一个list的第一个元素作为head
2,如果这个head不出现在其他list的尾部,则它是一个“好头”,可以从merge()中移出来
3,否则,取出下一个list中的第一个元素作同样的判断
4,重复上述过程直至所有的类都移到merge()算子的外部则构建MRO完成
5,否则,改继承结果无法生成MRO
所以对于L[F(A, B)] = F + merge(L[A], L[B], A, B)这个表达式,L[A], L[B]可以先按照L[]算法展开为:
L[A]=L[A(X, Y)]=A+merge(L[X],L[Y],X,Y)=A+merge(X,Y,X,Y)=A,X,Y
L[B]=L[B(Y, X)]=B+merge(L[Y],L[X],Y,X)=B+merge(Y,X,Y,X)=B,Y,X
例如这里的merge(X,Y,X,Y)首先判断X,因为X不在其他list的尾部(X算是list的头部)所以先提取X出来,这时候变成了A,X+merge(Y,Y)显然Y也能直接提取出来了;merge(Y,X,Y,X)同理。
把这俩结果代回去,总式子为:
L[F(A,B)] = F + merge( (A,X,Y), (B, Y, X), A, B)
这时候先判断A,因为不在其他list的尾部,所以提出出来式子变为:
F,A + merge((X, Y), (B, Y, X), B)
再判断第二个list的第一个元素B,也不在其他list的尾部,所以提出来:
F,A,B + merge((X, Y), (Y, X))
接着第二轮判断第一个list的头元素X,结果在第二个list中发现了X在尾部不能提取;再判断Y*结果发现在第一个list的尾部也不行。所以最终就遇到了不可构建MRO的情况!
结论
可见,虽然python的多重继承非常强大但是必须小心注意继承顺序(避免上述章节中提及的MRO不可构建的继承结构),与Java这种单继承语言不同 - super()总是沿着继承链向上追溯。python中方法的super()并不总是指向其声明的父类的同名方法,而是沿着MRO从左到往的传播。