非线性动力学笔记C2.6-2.8震荡,势,数值求解
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- C2 一维流动
-
- 2.6 一维流动中震荡(oscillation)的不可能性
-
- 机械类比
- 2.7 势(Potential)
-
- 例2.7.2
- 2.8 数值求解(numerical solution)
-
- 2.8.1 欧拉方法
- 2.8.2 例子
前言
提示:这里可以添加本文要记录的大概内容:
参考书《Nonlinear dynamics and chaos》 Steven H. Strogatz
本节重点Note第二章2.6-2.8震荡,势,数值求解内容,图片来自于该书
C2 一维流动
2.6 一维流动中震荡(oscillation)的不可能性
不动点会主导一节系统的动力学,目前我们看到所有的轨迹,要不接近一个不动点,要么向无穷远处发散。事实上,在一条直线上仅可能发生两种情况,因为轨迹会沿着一个方向单调增加或降低,或保持不变。从更几何的角度来说,相点(phase point)从不方向。也就是说,从更几何的角度来说,一维情况相点从不方向。不动点可以看作平衡解,二趋于平衡解的方式是单调的,在到达平衡点之前不会出现过冲(超出平衡位置,overshot)和阻尼振荡(damped oscillation).因此不存在周期性震荡的解。
注意,这里的 x ˙ = f ( x ) \dot{x}=f(x) x˙=f(x)对应的是一条直线上的运动。而面对二维运动,如一个圆,则有可能回到起始位置。
机械类比
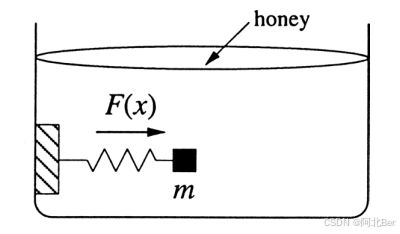
我们将 x ˙ = f ( x ) \dot{x}=f(x) x˙=f(x)看作牛顿定律中的一个特殊情况,此时惯性项可以忽略。
举例,假定质量 m m m由于连接在一个非线性的弹簧上,受到一个恢复力 F ( x ) F(x) F(x),假设该装置浸润在一个非常粘的液体之后,受到一个阻尼力 b x ˙ b\dot{x} bx˙,那么它的控制方程为 m x ¨ + b x ˙ = F ( x ) m\ddot{x} + b\dot{x} = F(x) mx¨+bx˙=F(x)如果粘性阻尼项相对于惯性项非常大,我们可以观察到 m x ¨ m\ddot{x} mx¨可以忽略. 那么控制方程可以近似看作 x ˙ = f ( x ) = b − 1 F ( x ) \dot{x}=f(x)=b^{-1}F(x) x˙=f(x)=b−1F(x)在这种情况下,物体倾向于停留在平衡位置,如果发生了微小的位移偏离平衡位置,由于粘性力很大,被拉离平衡位置后会缓慢回复,由于阻尼(damping)非常大,因此不会发生震荡(oscilaation)。
2.7 势(Potential)
对于方程 x ˙ = f ( x ) \dot{x}=f(x) x˙=f(x),一个颗粒从势能较高(potential wall)的地方滑下来
那么我们定义一个势(potential) V ( x ) V(x) V(x)满足
f ( x ) = − d V d x f(x) = -\frac{dV}{dx} f(x)=−dxdV
由于 d V d t = d V d x d x d t \frac{dV}{dt} = \frac{dV}{dx} \frac{dx}{dt} dtdV=dxdVdtdx
我们可以得到对于一阶系统而言 d x d t = − d V d t \frac{dx}{dt} = -\frac{dV}{dt} dtdx=−dtdV
由于 x ˙ = − d V d x \dot{x} = -\frac{dV}{dx} x˙=−dxdV
我们可以得到 d V d t = − ( d V d x ) 2 ≤ 0 \frac{dV}{dt} = - (\frac{dV}{dx})^2 \leq 0 dtdV=−(dxdV)2≤0
也就是说势(potential)会随着轨迹而逐渐减少,而颗粒会最终向势较低的方向运动. 当运动到 d V d x = 0 \frac{dV}{dx}=0 dxdV=0的位置时颗粒停止运动,即达到平衡点/不动点. 也就是说对于一个势函数 V ( x ) V(x) V(x)的局部极小值(local minimum) 会对应一个稳定不动点(stable fixed point),而势函数 V ( x ) V(x) V(x)的局部极大值(local maximum)对应一个不稳定不动点(unstable fixed point).
例2.7.2
给定系统 x ˙ = x − x 3 \dot{x}=x-x^3 x˙=x−x3我们可以通过分析势得到平衡位置
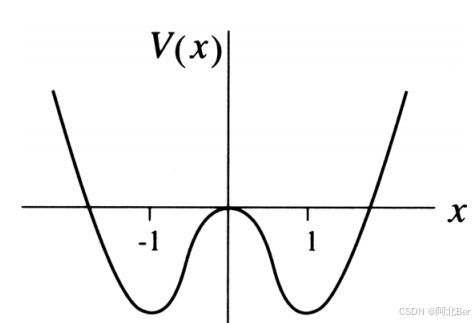
通过解方程 − d V d x = x − x 3 -\frac{dV}{dx} = x - x^3 −dxdV=x−x3 我们可以得到 V = − 1 2 x 2 + 1 4 x 4 + C V = -\frac{1}{2}x^2 + \frac{1}{4}x^4 + C V=−21x2+41x4+C。我们再次设 C = 0 C = 0 C=0。可以得到如下关于 V V V 的图像。在 x = ± 1 x = \pm 1 x=±1处的局部最小值对应于稳定平衡,而在 x = 0 x = 0 x=0 处的局部最大值对应于不稳定平衡。图中显示的势能通常被称为双井势(double-well potential),并且该系统是双稳态的,因为它有两个稳定的平衡点。
2.8 数值求解(numerical solution)
2.8.1 欧拉方法
数值求解的目的是在于求解方程的近似解。
我们可以用如下方式描述该问题:给定微分方程 x ˙ = f ( x ) \dot{x} = f(x) x˙=f(x),在 t = t 0 t = t_0 t=t0 时满足条件 x = x 0 x = x_0 x=x0,找到一个方法来求近似解 x ( t ) x(t) x(t)。
假设我们使用 x ˙ = f ( x ) \dot{x} = f(x) x˙=f(x) 的向量场解释。也就是说,我们想象在 x x x 轴上有一个速度场,位置 x x x 的速度为 f ( x ) f(x) f(x)。想象我们正随着一个相点被流体携带向下游移动。最初我们在 x 0 x_0 x0,局部速度为 f ( x 0 ) f(x_0) f(x0)。如果我们流动一小段时间 Δ t \Delta t Δt,我们将移动距离 f ( x 0 ) Δ t f(x_0)\Delta t f(x0)Δt,因为距离 = 速率 × 时间。当然,这并不完全正确,因为我们的速度在整个步骤中发生了一些变化。但在足够小的步骤中,速度将几乎恒定,我们的近似应该是相当好的。因此,我们的新位置 x ( t 0 + Δ t ) x(t_0 + \Delta t) x(t0+Δt) 大约是 x 0 + f ( x 0 ) Δ t x_0 + f(x_0)\Delta t x0+f(x0)Δt。让我们称这个近似为 x 1 x_1 x1。因此
x ( t 0 + Δ t ) ≈ x 1 = x 0 + f ( x 0 ) Δ t . x(t_0 + \Delta t) \approx x_1 = x_0 + f(x_0)\Delta t. x(t0+Δt)≈x1=x0+f(x0)Δt.
现在我们迭代。我们的近似将我们带到一个新的位置 x 1 x_1 x1;我们的新速度是 f ( x 1 ) f(x_1) f(x1);我们向前移动到 x 2 = x 1 + f ( x 1 ) Δ t x_2 = x_1 + f(x_1)\Delta t x2=x1+f(x1)Δt;依此类推。一般来说,更新规则是
x n + 1 = x n + f ( x n ) Δ t . x_{n+1} = x_n + f(x_n)\Delta t. xn+1=xn+f(xn)Δt.
这是最简单的数值积分方案。它被称为欧拉方法。
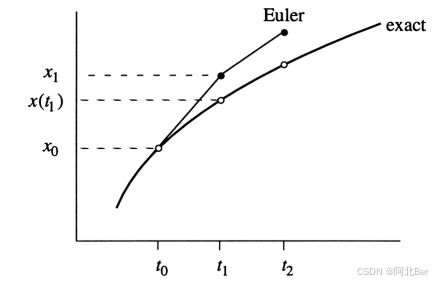
欧拉方法可以通过绘制 x x x 与 t t t 的关系图来直观化。曲线显示了精确解 x ( t ) x(t) x(t),而空心点显示了在离散时间 t n = t 0 + n Δ t t_n = t_0 + n\Delta t tn=t0+nΔt 处的值 x ( t n ) x(t_n) x(tn)。黑色点显示了由欧拉方法给出的近似值。我们可以发现,除非 Δ t \Delta t Δt 非常小,否则近似很快就会变得很差。因此,欧拉方法在实践中并不推荐使用,但是这是一种比较基本直观的思路,实际应用中会使用龙格-库塔法(Runge-Kutta methods)等误差更小的方法。
2.8.2 例子
对 x ˙ = x ( 1 − x ) \dot{x}=x(1-x) x˙=x(1−x)进行数值求解
我们可以得到如下向量场

其中 x = 1 x=1 x=1是一个不动点