写在前面:
对Metal技术感兴趣的同学,可以关注我的专题:Metal专辑
也可以关注我个人的账号:张芳涛
所有的代码存储的Github地址是:Metal
正文
本篇文章只要介绍一些基本的数学函数在图形绘制中的实际运用。
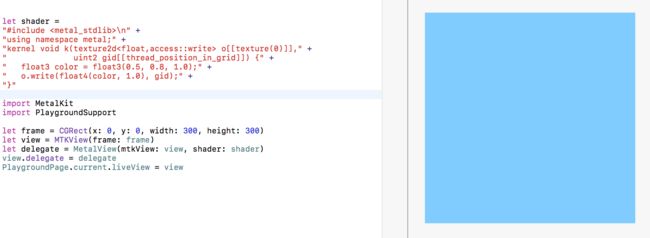
我们还是使用playground来开发。先创建一个MetalView.swift。第一步,先把蓝色的天空绘制出来:
let shader =
"#include \n" +
"using namespace metal;" +
"kernel void k(texture2d o[[texture(0)]]," +
" uint2 gid[[thread_position_in_grid]]) {" +
" float3 color = float3(0.5, 0.8, 1.0);" +
" o.write(float4(color, 1.0), gid);" +
"}"
效果图如下:
为了更逼真一些,我们需要一个渐变色。我们将当前像素坐标划分为屏幕尺寸,我们得到UV - 一对浮点数(0-1)。然后我们将固定颜色与Y相乘- 其垂直分量UV为我们提供渐变:
" int width = o.get_width();" +
" int height = o.get_height();" +
" float2 uv = float2(gid) / float2(width, height);" +
" color *= uv.y;" +
效果图:
看上去还可以,不过好像并不是很像真正的天空。让我们使用颜色混合技术来模拟一个真正的黄昏时候的天空:
" float3 color = mix(float3(1.0, 0.6, 0.1), float3(0.5, 0.8, 1.0), sqrt(1 - uv.y));" +
效果图:
接下来我们使用smootstep绘制一个内部为黑色,外部为蓝色且r与(r + 0.01)之间的混合颜色的圆形。将最后一行替换为:
" float r = 0.2;" +
" color *= smoothstep(r, r + 0.01, length(q));" +
效果图:
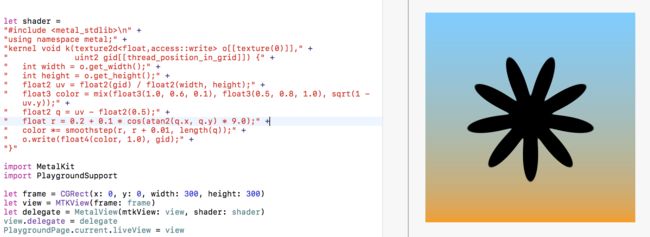
因为我们希望这个圆形区域内部可以形成一些树叶之类的形状,如果我们对圆形周长不满意,我们可以通过使用cos和atan2等数学函数使其变得崎岖不平。我们在这里生成9个尖峰(frequency),尖峰长度(amplitude)为0.1:
" float r = 0.2 + 0.1 * cos(atan2(q.x, q.y) * 9.0);" +
效果图:
这更像是一朵花,而不是树叶,通过如下代码,让图形看起来更自然一些
" float r = 0.2 + 0.1 * cos(atan2(q.x, q.y) * 9.0 + 20.0 * q.x);" +
现在是垂直向下的效果,我们可以对这个图形稍微旋转一下,来使得看上去更逼真:
" float r = 0.2 + 0.1 * cos(atan2(q.x, q.y) * 9.0 + 20.0 * q.x + 1.0);" +
树冠绘制完了,下面我们来绘制树干:
" r = 0.015;" +
" color *= smoothstep(r, r + 0.002, abs(q.x));" +
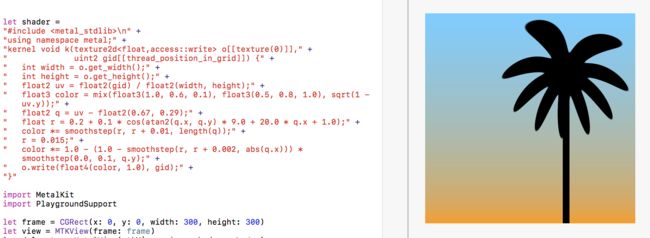
我们可以通过在Y坐标上使用另一个smoothstep来删除不需要的部分:
" color *= 1.0 - (1.0 - smoothstep(r, r + 0.002, abs(q.x))) * smoothstep(0.0, 0.1, q.y);" +
效果图:
由于树冠和树干都使用q,因此修改其值将同时移动:
" float2 q = uv - float2(0.67, 0.29);" +
这可怎么办?sin函数了解一下:sin函数可以用来弯曲树干:我们用2.0的倍数来实现树干的弯曲效果,0.25的振幅也可以让树根和树干之间有平移:
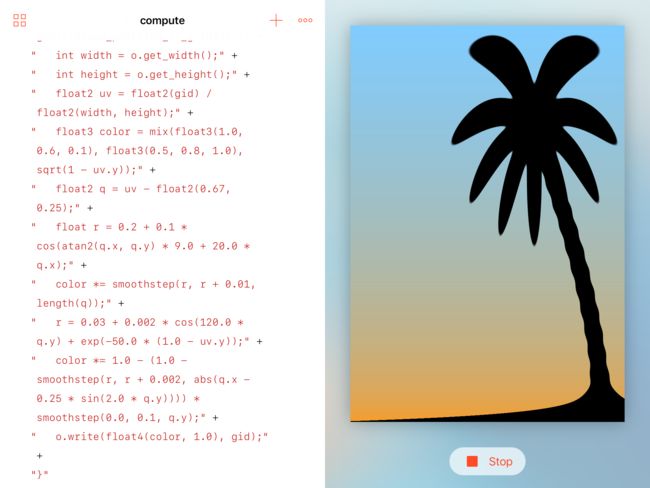
" color *= 1.0 - (1.0 - smoothstep(r, r + 0.002, abs(q.x - 0.25 * sin(2.0 * q.y)))) * smoothstep(0.0, 0.1, q.y);" +!
如果你满意的话,这样也够了。最起码一棵树显示出来了,不过我们还可以对树干进行一下优化,目前树干太平滑了,我们需要让树干有点破浪装的起伏,
cos函数可以解决这个问题:
" r = 0.015 + 0.002 * cos (120.0 * q.y);" +
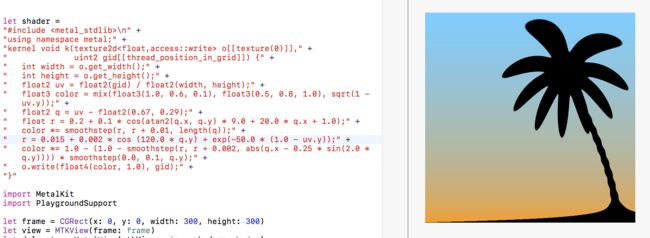
最后再弄一个地面,这个效果需要用到exp函数
" r = 0.015 + 0.002 * cos (120.0 * q.y) + exp(-50.0 * (1.0 - uv.y));" +
我们可以通过使用sqrt函数增加第二种颜色的存在:
" float3 color = mix(float3(1.0, 0.6, 0.1), float3(0.5, 0.8, 1.0), sqrt(1 - uv.y));" +
总之,我们看到如何使用sqrt来形成过渡,然后使用cos来创建形状的起伏变化,然后使用exp来创建曲线,然后使用smoothstep进行阈值处理,然后使用abs进行对称并混合进行混合。
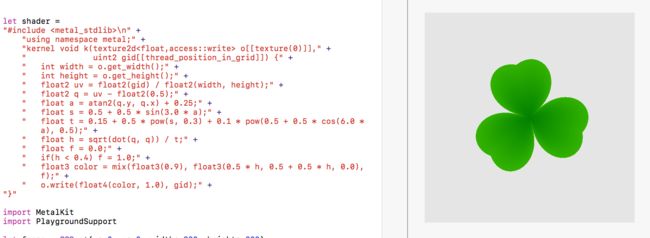
根据上面的说明,绘制一个三叶草,下面的代码可以实现:
"#include \n" +
"using namespace metal;" +
"kernel void k(texture2d o[[texture(0)]]," +
" uint2 gid[[thread_position_in_grid]]) {" +
" int width = o.get_width();" +
" int height = o.get_height();" +
" float2 uv = float2(gid) / float2(width, height);" +
" float2 q = uv - float2(0.5);" +
" float a = atan2(q.y, q.x) + 0.25;" +
" float s = 0.5 + 0.5 * sin(3.0 * a);" +
" float t = 0.15 + 0.5 * pow(s, 0.3) + 0.1 * pow(0.5 + 0.5 * cos(6.0 * a), 0.5);" +
" float h = sqrt(dot(q, q)) / t;" +
" float f = 0.0;" +
" if(h < 0.4) f = 1.0;" +
" float3 color = mix(float3(0.9), float3(0.5 * h, 0.5 + 0.5 * h, 0.0), f);" +
" o.write(float4(color, 1.0), gid);" +
"}"
效果图:
代码点击我