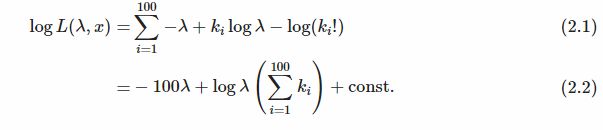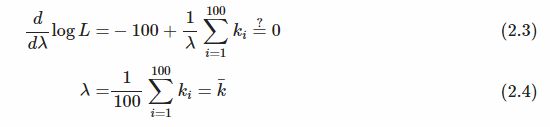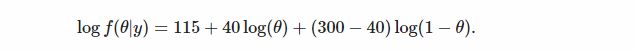《Modern Statistics for Modern Biology》Chapter 一: 离散数据模型的预测(1.1 - 1.3)
《Modern Statistics for Modern Biology》Chapter 一: 离散数据模型的预测(1.4 - 1.5)
《Modern Statistics for Modern Biology》Chapter 二: 统计建模(2.1-2.3)
从这章开始最开始记录一些markdown等小知识
$\hat{p}=\frac{1}{12}$:
掌握R语言中的apply函数族
2.3.1 经典数据的经典统计
-
下面是我们的计算结果的一个正式证明,即平均值使(log-)似然最大
-
我们使用包罗万象的
“const”。对于不依赖于λ的式子(尽管它们确实依赖于x,也就是依赖于ki)。为了找到最大化这一点的λ,我们计算λ中的导数并将其设置为零。
您刚刚看到了统计方法的第一步,从“从头开始”(从数据开始)来推断模型参数:这是从数据中对参数进行的统计估计。另一个重要的组成部分将是选择我们的数据属于哪种分布,这部分是通过评估拟合的优良度来完成的。我们稍后会遇到这个问题。
在经典的统计检验框架中,我们为数据考虑了一个单一的模型,我们称之为零假设模型。零假设模型建立了一个“乏味”的基线,例如,所有的观测数据都来自相同的随机分布,而不管它们来自哪一组或来自哪种处理。然后,我们通过计算数据与该模型兼容的概率来测试是否有更有趣的事情正在进行。通常,这是我们所能做的最好的事情,因为我们不知道什么是“有趣的”、非空的或可供选择的模型。在其他情况下,我们有两个相互竞争的模型,我们可以比较,我们将在稍后看到。
► 问题 2.6
- 使用已知分布进行建模的价值是什么?例如,为什么知道一个变量的泊松分布是有趣的呢?
► 解
另一个有用的方向是回归。我们可能有兴趣知道我们的基于计数的反应变量(例如,计数序列读取的结果)如何取决于连续的协变量,例如温度或养分浓度。您可能已经遇到了线性回归,其中我们的模型是,响应变量y依赖于协变量x,通过方程y=ax+b+e,参数a和b(我们需要估计),以及
残差e,其概率模型是正态分布(我们通常也需要估计其方差)。对于计数数据,同样类型的回归模型也是可能的,尽管残差的概率分布需要是非正态的。在这种情况下,我们使用广义线性模型框架。在第8章中,我们将看到研究RNA-Seq的例子,在第9章,我们将看到另一种类型的下一代测序数据,16S rRNA数据。知道我们的概率模型涉及泊松、二项、多项分布(从这里开始就使用多项吧!!)或其他参数系列,将使我们能够快速回答有关模型参数的问题,并计算
p值和置信区间等数量。
2.4 二项分布与极大似然
- 在一个二项分布中有两个参数:试验次数n,这通常是已知的,和在试验中看到1的概率p。这种可能性通常是未知的。
2.4.1 举例
- 假设我们选取
n = 120名男性测试他们是否为红绿色盲。如果不是红绿色盲就用代码0表示,否则用1。得到数据如下:
> cb <- c(rep(0,110),rep(1,10)) ## 由于这里没找到原始数据,所以就自己生成了一组结果
> table(cb)
cb
0 1
110 10
► 问题 2.7
- 根据这些数据,p的哪个值最有可能?
► 解
在这种特殊的情况下,你的直觉可能会给出估计,这就是最大似然估计。我们给这封信戴上帽子,提醒我们这不一定是潜在的真实价值,而是我们根据数据所作的估计。
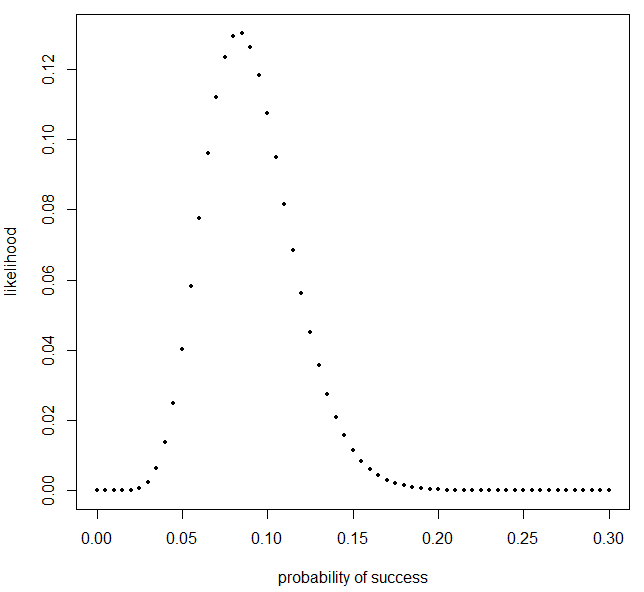
和以前的泊松分布一样,如果我们计算出许多可能的p的可能性,我们可以画出它,看看它的最大值落在哪里。
> probs = seq(0, 0.3, by = 0.005) ## 从0开始到3结束,以0.005为间隔生成一组数据
> likelihood = dbinom(sum(cb), prob = probs, size = length(cb))
> plot(probs, likelihood, pch = 16, xlab = "probability of success",
+ ylab = "likelihood", cex=0.6)
> probs[which.max(likelihood)]
[1] 0.085
- 注:0.085不完全是我们预期的值,这是因为我们尝试的一组值(在
probs中)不包括 ≃ 0.0833的确切值,因此我们得到了第二个最好的值。我们可以使用数值优化方法来克服这一点。
二项分布的似然
- 可能性和概率是相同的数学函数,只是以不同的方式解释-在一种情况下,它告诉我们在给定参数的情况下,看到一组特定的数据值的可能性有多大;在另一种情况下,我们认为数据是固定的,并要求提供使数据更有可能发生的特定参数值。假设
n=300,我们观察到y=40个成功。然后,对于二项分布:
- 因为非常大,它大约是,这可以从Stirling公式中看出。我们也可以用R:
choose(300,40) = 9.8e+49。,我们用似然的对数给出:
- 定义的函数如下:
> loglikelihood = function(theta, n = 300, k = 40) {
+ 115 + k * log(theta) + (n - k) * log(1 - theta)
+ }
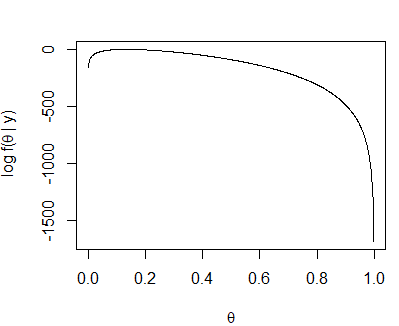
- 我们为从0到1的θ范围绘制图:
> thetas = seq(0, 1, by = 0.001)
> plot(thetas, loglikelihood(thetas), xlab = expression(theta),
+ ylab = expression(paste("log f(", theta, " | y)")), type = "l") ## expression表达式的使用值得好好学习
- 最大值位于
40/300=0.1333…,这与直觉是一致的,但是我们看到,θ的其他值几乎也是一样的,因为函数在最大值附近是相当平坦的。在后面的章节中,我们将看到贝叶斯方法如何允许我们对θ使用一系列的值。
2.5 More boxes:multinomial data(理解是多个box的多项分布数据)
2.5.1 DNA计数模型:碱基对
- DNA有四种碱基分子:
A-腺嘌呤、C-胞嘧啶、G-鸟嘌呤、T-胸腺嘧啶。核苷酸分为两类:嘌呤(A和G)和嘧啶(C和T)。嘌呤/嘧啶 可以使用二项分布模型进行计算,但是A/C/G/T不行。所以我们需要使用来源1.4的多项分布模型。
2.5.2 Nucleotide bias(碱基偏差)
- 这一部分结合了估计和测试的仿真在一个实际的例子。来自金黄色葡萄球菌基因的一条dna的数据可以在
fasta文件staphSequence.ffn.txt中找到, 我们可以通过bioconductor包Biostrings读取数据:
Biostrings这个包也得好好学啊 !!
setwd("e://compute language/NGS/Modern Statistics for Modern Biology/data/")
> library(Biostrings)
> staph = readDNAStringSet("staphsequence.ffn.txt", "fasta")
> staph[1]
A DNAStringSet instance of length 1
width seq names
[1] 1362 ATGTCGGAAAAAGAAATTTGGGAAAAAGTGCTTGAA...TAGAGAATCTTGAAAAAGAAATAAGAAATGTATAA lcl|NC_002952.2_c...
> letterFrequency(staph[[1]], letters = "ACTG", OR = 0)
A C T G
522 219 392 229
► 问题 2.8 Why did we use double square brackets in the second line?
-
双括号[[i]]将第i个基因的序列提取为DNAString,而不是一对单方括号[i],后者返回只有一个DNAString的DNAStringSet。如果看staph[1]的长度,它是1,而staph[[1]]的长度是1362。
► 问题 2.9 按照类似于练习1.8的步骤,测试第一个基因的核苷酸是否在四个核苷酸之间均匀分布。
- 由于它们不同的物理性质,进化选择可以作用于核苷酸频率。所以我们可以问,比如说,从这些数据中得到的前十个基因是否来自同一个多项式。我们没有事先的参考,我们只想确定核苷酸是否在前10个基因中以相同的比例出现。如果不是,这将为我们对这10个基因施加不同的选择性压力提供证据。
vapply(X, FUN, FUN.VALUE, ..., USE.NAMES = TRUE): 掌握R语言中的apply函数族
参数列表:
-
X:数组、矩阵、数据框 -
FUN: 自定义的调用函数 -
FUN.VALUE: 定义返回值的行名row.names -
…: 更多参数,可选 -
USE.NAMES: 如果X为字符串,TRUE设置字符串为数据名,FALSE不设置
> letterFrq = vapply(staph, letterFrequency, FUN.VALUE = numeric(4), letters = "ACGT", OR = 0)
> colnames(letterFrq) = paste0("gene", seq(along = staph))
>computerProportions = function(x){x/sum(x)}
> prop10 = apply(tab10, 2, computerProportions) ## 2表示列
> round(prop10, digits = 2)
gene1 gene2 gene3 gene4 gene5 gene6 gene7 gene8 gene9 gene10
A 0.38 0.36 0.35 0.37 0.35 0.33 0.33 0.34 0.38 0.27
C 0.16 0.16 0.13 0.15 0.15 0.15 0.16 0.16 0.14 0.16
G 0.17 0.17 0.23 0.19 0.22 0.22 0.20 0.21 0.20 0.20
T 0.29 0.31 0.30 0.29 0.27 0.30 0.30 0.29 0.28 0.36
> p0 = rowMeans(prop10)
> p0
A C G T
0.3470531 0.1518313 0.2011442 0.2999714
- 因此,假设
p0是所有十个基因的多项概率的向量,并使用蒙特卡罗模拟来检验在这个假设下观察到的字母频率和期望值之间的偏差是否在一个合理的范围内。 - 我们通过取概率向量
p0的outer函数求外积和10列中的每一列的核苷酸计数之和来计算期望的计数。
> cs = colSums(tab10)
> cs
gene1 gene2 gene3 gene4 gene5 gene6 gene7 gene8 gene9 gene10
1362 1134 246 1113 1932 2661 831 1515 1287 696
> expectedtab10 = outer(p0, cs, FUN = "*") ## * 表示乘以,这里还可以用“+”、“-”表示
> round(expectedtab10)
gene1 gene2 gene3 gene4 gene5 gene6 gene7 gene8 gene9 gene10
A 473 394 85 386 671 924 288 526 447 242
C 207 172 37 169 293 404 126 230 195 106
G 274 228 49 224 389 535 167 305 259 140
T 409 340 74 334 580 798 249 454 386 209
小插曲 : outer函数
- 现在,我们可以使用
rmultinom函数创建一个包含正确列和的随机表。该表是根据实际比例由p0给出的零假设生成的。
> randomtab10 = sapply(cs, function(s) {rmultinom(1, s, p0)}) # n = 1表示看过程。 size = 1表示只看结果
> all(colSums(randomtab10) == cs)
[1] TRUE
- 现在我们重复这个
B=1000次。对于每个表,我们从第1章(函数stat)的1.4.1节计算我们的测试统计信息,并将结果存储在向量simulstat中。这些值共同构成了我们的零假设分布,因为它们是在p0是10个基因中每个基因的多项比例的向量这一零假设下生成的。
> stat = function(obsvd, exptd = 20 * pvec){
+ sum((obsvd - exptd)^2 / exptd)
+ }
> B = 1000
> simulstat = replicate(B, {
+ randomtab10 = sapply(cs, function(s) {rmultinom(1, s, p0)})
+ stat(randomtab10, expectedtab10)
+ })
> S1 = stat(tab10, expectedtab10)
> S1
[1] 70.07533
> sum(simulstat >= S1)
[1] 0
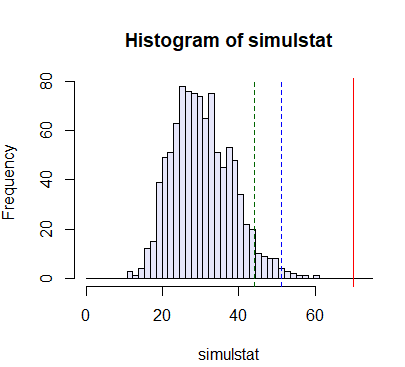
> hist(simulstat, col = "lavender", breaks = seq(0, 75, length.out = 50))
> abline(v = S1, col = "red")
> abline(v = quantile(simulstat, probs = c(0.95, 0.99)),
+ col = c("darkgreen", "blue"), lty = 2)
- 直方图如
图2.7所示。我们看到,在零假设模型下,看到一个大到s1=70.1的值的概率是非常小的。在我们的1000次模拟中,发生了0次出现了与S1一样大的值。因此,这十个基因似乎不是来自同一个多项式模型。