ML-感知器-线性回归-逻辑回归学习

欧式距离

import numpy as np
import math

a = np.random.rand(100)
b = np.random.rand(100)

math.sqrt(np.dot((a-b),(a-b)))

4.161071187845777

曼哈顿距离

np.sum(np.abs(a-b))

34.732195473330904

切比雪夫距离

np.max(np.abs(a-b))

0.9645497259276183

余弦夹角

np.dot(a,b)/((math.sqrt(np.dot(a,a)))+math.sqrt(np.dot(b,b)))

2.1019060661351556

np.dot(a,b)/(np.linalg.norm(a)+np.linalg.norm(b))

2.1019060661351556

线性回归 (欧氏距离)

import numpy as np
import matplotlib.pyplot as plt
import seaborn

W = np.random.rand(10,1)
T = np.random.rand(10,10)
b = 1

np.dot(W.T,T)+b

array([[4.84724558, 3.81349989, 4.01291752, 2.96597734, 5.11944271,
        4.06417777, 3.49035802, 3.43582066, 4.38419865, 4.04254153]])

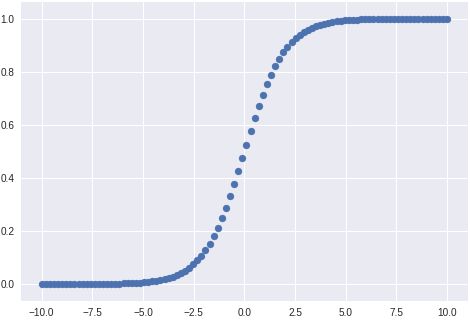
def sigmoid(x):
    return (1 / (1 + np.exp(-x)))

X = np.linspace(-10,10,num=100)
# X = np.random.rand(1000)
Y = [sigmoid(i) for i in X]
X
plt.scatter(X,Y)
plt.show()

image.png

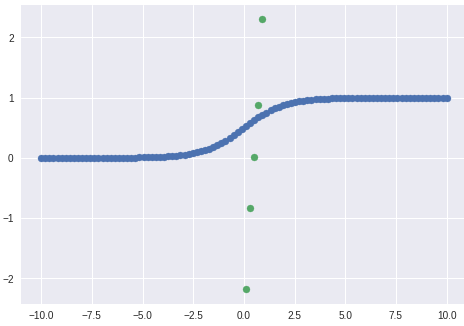
scipy sigmode 函数

from scipy.special import expit, logit

Y = expit(X)
Y1 = logit(X)
plt.scatter(X,Y)
plt.scatter(X,Y1,marker="o")

plt.show()

image.png

numpy 的 revel 和 flatten

a = np.array([[1,2,3],[4,5,6]])
a.ravel() #  ravel 返回视图
a.flatten() # flatten 返回拷贝

array([1, 2, 3, 4, 5, 6])

from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LogisticRegressionCV
lr = LogisticRegressionCV()
X = np.linspace(1,100,100)
X = [[i] for i in X]
y = 50*[0]+50*[1]
lr.fit(X,y)

meshgrid 用来生成网格

np.meshgrid([1,2,3],[4,5,6])

[array([[1, 2, 3],
        [1, 2, 3],
        [1, 2, 3]]), array([[4, 4, 4],
        [5, 5, 5],
        [6, 6, 6]])]

import numpy as np
from sklearn import linear_model
from sklearn import svm

classifiers = [
#     svm.SVR(),
    linear_model.SGDRegressor(),
    linear_model.BayesianRidge(),
    linear_model.LassoLars(),
    linear_model.ARDRegression(),
    linear_model.PassiveAggressiveRegressor(),
    linear_model.TheilSenRegressor(),
    linear_model.LinearRegression()]



for item in classifiers[:1]:
    print(item)
    clf = item
    clf.fit(trainingData, trainingScores)
    print(clf.predict(predictionData),'\n')

from sklearn import linear_model
import numpy as np
clf = linear_model.LinearRegression()

trainingData    = np.array([ [2.3, 4.3, 2.5],  [1.3, 5.2, 5.2],  [3.3, 2.9, 0.8],  [3.1, 4.3, 4.0]  ])
trainingScores  = np.array( [1, 1, 1, 1] )
predictionData  = np.array([ [2.5, 2.4, 2.7],  [2.7, 3.2, 1.2] ])

clf.fit([[1],[1],[1]], [1,2,3])