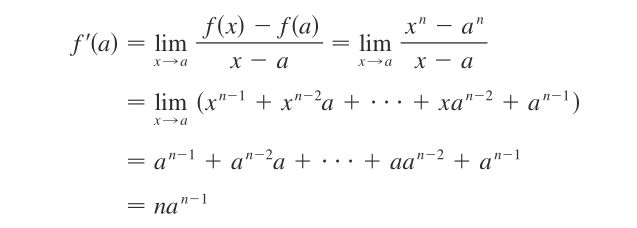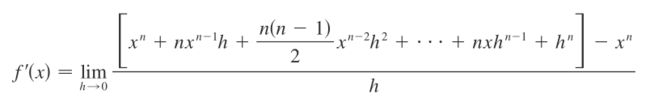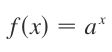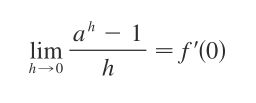- Python教程:一文了解使用Python处理XPath
旦莫
Python进阶python开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath?2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
- 数据结构 | 栈和队列
TT-Kun
数据结构与算法数据结构栈队列C语言
文章目录栈和队列1.栈:后进先出(LIFO)的数据结构1.1概念与结构1.2栈的实现2.队列:先进先出(FIFO)的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中,栈和队列是两种基本且重要的数据结构,它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
- 科幻游戏 《外卖员模拟器》 主要地理环境设定 (1)
穷人小水滴
游戏科幻设计
游戏名称:《外卖员模拟器》(英文名称:waimai_se)作者:穷人小水滴本故事纯属虚构,如有雷同实属巧合.故事发生在一个(架空)平行宇宙的地球,21世纪(超低空科幻流派).相关文章:https://blog.csdn.net/secext2022/article/details/141790630目录1星球整体地理设定2巨蛇国主要设定3海蛇市主要设定3.1主要地标建筑3.2交通3.3能源(电力)
- 00. 这里整理了最全的爬虫框架(Java + Python)
有一只柴犬
爬虫系列爬虫javapython
目录1、前言2、什么是网络爬虫3、常见的爬虫框架3.1、java框架3.1.1、WebMagic3.1.2、Jsoup3.1.3、HttpClient3.1.4、Crawler4j3.1.5、HtmlUnit3.1.6、Selenium3.2、Python框架3.2.1、Scrapy3.2.2、BeautifulSoup+Requests3.2.3、Selenium3.2.4、PyQuery3.2
- 3.1 损失函数和优化:损失函数
做只小考拉
用一个函数把W当做输入,然后看一下得分,定量地估计W的好坏,这个函数被称为“损失函数”。损失函数用于度量W的好坏。有了损失函数的概念后,就可以定量的衡量W到底是好还是坏,要找到一种有效的方法来从W的可行域里,找到W取何值时情况最不坏,,这个过程将会是一个优化过程。损失函数L_i定义:通过函数f给出预测的分数和真实的目标(或者说是标签y),可以定量的描述训练样本预测的好不好,最终的损失函数是在整个数
- HarmonyOS Next鸿蒙扫一扫功能实现
JohnLiu_
HarmonyOSNextharmonyos华为扫一扫鸿蒙
直接使用的是华为官方提供的api,封装成一个工具类方便调用。import{common}from'@kit.AbilityKit';import{scanBarcode,scanCore}from'@kit.ScanKit';exportnamespaceScanUtil{exportasyncfunctionstartScan(context:common.Context):Promise{if
- 探索ASPICE V3.1:汽车行业软件开发的中文指南
阮懿同
探索ASPICEV3.1:汽车行业软件开发的中文指南ASPICE_V3.1中文版.pdf.zip项目地址:https://gitcode.com/open-source-toolkit/422a2在汽车软件工程领域,高质量的标准对于确保行车安全和提升用户体验至关重要。今天,我们为您介绍一个珍贵的开源宝藏——ASPICEV3.1中文版资源。这是一篇专为国内汽车行业开发者、质量管理者准备的深度解读,旨
- 前端知识点
ZhangTao_zata
前端javascriptcss
下面是一个最基本的html代码body{font-family:Arial,sans-serif;margin:20px;}//JavaScriptfunctionthatdisplaysanalertwhencalledfunctionshowMessage(){alert("Hello!Youclickedthebutton.");}MyFirstHTMLPageWelcometoMyPage
- Python OpenCV图像处理:从基础到高级的全方位指南
极客代码
玩转Python开发语言pythonopencv图像处理计算机视觉
目录第一部分:PythonOpenCV图像处理基础1.1OpenCV简介1.2PythonOpenCV安装1.3实战案例:图像显示与保存1.4注意事项第二部分:PythonOpenCV图像处理高级技巧2.1图像变换2.2图像增强2.3图像复原第三部分:PythonOpenCV图像处理实战项目3.1图像滤波3.2图像分割3.3图像特征提取第四部分:PythonOpenCV图像处理注意事项与优化策略4
- matlab游标标注移动,matlab实现图形窗口的数据游标
莫白想
matlab游标标注移动
DatacursorsforfigurewindowSeveralrelatedfunctions:CreateCursorsetsupaverticalcursoronallaxesinafigure.Thecursorscanbemovedaroundusingthemouse.MultiplecursorsaresupportedineachfigureGetCursorLocationre
- php状态监控源码,PHP服务器状态监控实现程序
江子星
php状态监控源码
*/header('Content-type:text/html;charset=utf-8');include'./smtp/class.smtp.php';include'./smtp/class.phpmailer.php';functionsendmail($subject='',$body=''){date_default_timezone_set('Asia/Shanghai');//
- 详解C语言中的循环语句
埋头编程~
C语言c语言开发语言
文章目录1.前言2.while循环2.1if和whlie的对比2.2while语句的工作机制2.3while循环的实践3.for循环3.1for循环语法3.2for循环的工作机制3.3for循环实践4dowhile循环4.1dowhlie循环语法4.2dowhile循环的工作机理4.3dowhile循环实践5.break和continue语句5.1break举例5.2continue举例6.got
- FPGA器件在线配置方法概述
fpga和matlab
FPGA其他fpga开发FPGA在线配置
目录1.配置电路结构和原理2.ICR控制电路软件3.几种常见的FPGA在线配置方法3.1动态部分重配置(PartialReconfiguration,PR)3.2在系统编程(In-SystemProgramming,ISP)3.3多比特流配置(Multi-BitstreamConfiguration)3.4远程更新与配置3.5使用OpenCL或HLS工具FPGA(Field-Programmabl
- Apache HBase基础(基本概述,物理架构,逻辑架构,数据管理,架构特点,HBase Shell)
May--J--Oldhu
HBaseHBaseshellhbase物理架构hbase逻辑架构hbase
NoSQL综述及ApacheHBase基础一.HBase1.HBase概述2.HBase发展历史3.HBase应用场景3.1增量数据-时间序列数据3.2信息交换-消息传递3.3内容服务-Web后端应用程序3.4HBase应用场景示例4.ApacheHBase生态圈5.HBase物理架构5.1HMaster5.2RegionServer5.3Region和Table6.HBase逻辑架构-Row7.
- 数据分析-24-时间序列预测之基于keras的VMD-LSTM和VMD-CNN-LSTM预测风速
皮皮冰燃
数据分析数据分析
文章目录1普通的LSTM模型1.1数据重采样1.2数据标准化1.3切分窗口1.4划分数据集1.5建立模型1.6预测效果2VMD-LSTM模型2.1VMD分解时间序列2.2对每一个IMF建立LSTM模型2.2.1IMF1—LSTM2.2.2IMF2-LSTM2.2.3统一代码2.3评估效果3CNN-LSTM模型3.1数据预处理3.2建立模型3.3效果预测4VMD-CNN-LSTM模型4.1VMD分解
- Swift4.0: 利用图形上下文画基础图?
Dayu大鱼
步骤:开启图片上下文获取上下文配置上下文3.1填充颜色cgColor3.2填充尺寸从图形上下文中获取图片关闭上下文返回图片importFoundationimportUIKitextensionUIImage{///画一个白色背景的图片classfuncimageWithWhiteBackGroundColor()->UIImage{//开始图形上下文UIGraphicsBeginImageCon
- Python 报错 ImportError: cannot import name xxx from partially initialized module xxx
SmallerFL
其他问题fixPython相关python深度学习pytorch人工智能
文章目录1.报错2.原因3.参考1.报错ImportError:cannotimportname'SummaryWriter'frompartiallyinitializedmodule'torch.utils.tensorboard'(mostlikelyduetoacircularimport)(/Library/Frameworks/Python.framework/Versions/3.1
- 2017.11.23打卡计划
爱跑步的coder
11.23打卡做完calculus_oneweek2的作业(暂时不学这个了,意义不大),并尽量将内容代码化。(已用python和ruby的匿名函数来表示)11.24打卡明晚学习中国人文文化导读第一周的课程。
- Spark集群的三种模式
MelodyYN
#Sparksparkhadoopbigdata
文章目录1、Spark的由来1.1Hadoop的发展1.2MapReduce与Spark对比2、Spark内置模块3、Spark运行模式3.1Standalone模式部署配置历史服务器配置高可用运行模式3.2Yarn模式安装部署配置历史服务器运行模式4、WordCount案例1、Spark的由来定义:Hadoop主要解决,海量数据的存储和海量数据的分析计算。Spark是一种基于内存的快速、通用、可
- python容器四之字典
@听风吟
Pythonpythonjavarpc大数据
文章目录1.字典介绍2.使用字典3.字典的常见操作3.1添加元素3.2删除元素3.3修改元素3.4查找元素4.字典遍历方法4.1遍历字典元素5.公共运算符6.公共方法1.字典介绍先来看看现实生活中的字典。我们知道,可以应用字典来查找汉字。在这里插入图片描述接着,来看看Python中的字典。比如,定义一个本书:{"name":"新华字典","page":568,"price":46.5}仔细观察,会
- SQLServer2022新特性 GENERATE_SERIES函数
zxrhhm
sqlserver数据库
SQLServer2022新特性GENERATE_SERIES函数,在给定间隔内生成一系列数字。序列值之间的间隔和步骤由用户定义。参考官方地址https://learn.microsoft.com/en-us/sql/t-sql/functions/generate-series-transact-sql?view=sql-server-ver161、本文内容语法参数返回类型权限示例相关内容适用于
- 从零开始学PostgreSQL (十三):并行查询
DBA实战
postgresql数据库
目录概述1.并行查询的工作原理2.什么时候可以使用并行查询?3.并行计划3.1.并行扫描3.2.并行连接3.3.并行聚合3.4.并行追加3.5.并行计划提示4.并行安全4.1.函数和聚合的并行标签5.注意事项6.总结概述并行查询是PostgreSQL提供的一种功能,它允许查询在多个CPU核心或处理器上同时执行,从而显著提高查询性能,特别是在处理大型数据集时。并行查询的设计目标是在多核处理器的现代硬
- NoClassDefFoundError: org.apache.poi.POIXMLDocument问题排查解决
qinmingjun718
apache
java.lang.NoClassDefFoundError:org/apache/poi/POIXMLDocumentPart这错很明显就是没找到这个类POIXMLDocumentPart就是找不到类问题原因是大概是因为poi从3.1.X低版本版本升级到pio4.1.2高版本的后与org.apache.poi.xwpf.converter.core-1.0.6.jar不兼容问题,导致这个情况的主
- SpringBoot3与SpringBoot2的区别
bjzhang75
springboot
文章目录1、JDK环境2、SpringFramework版本3、主要变化和新特性3.1配置变化3.2GraalVM3.3安全性改进3.4性能优化3.4.1启动时间3.4.2内存使用3.5改进的依赖管理3.6全新启动器3.7Kotlin支持SpringBoot3与SpringBoot2的区别1、JDK环境SpringBoot3最低要求JDK17SpringBoot2最低要求JDK82、SpringF
- MySQL8.0默认TCP端口介绍
zxrhhm
tcp/ip网络协议mysql
1、本文内容选择题TCP/IPMySQL8.0的默认TCP端口showvariables查看总结2、选择题A、3306B、33060C、33062D、330633、TCP/IPTCP/IP(TransmissionControlProtocol/InternetProtocol,传输控制协议/网际协议)是指能够在多个不同网络间实现信息传输的协议簇。以下是对TCP/IP协议的详细解释:3.1.定义与
- java unix网络编程_《UNIX网络编程 卷2:进程间通信(第2版)》PDF 下载
weixin_39688019
javaunix网络编程
图书目录:第一部分简介第1章简介1.1概述1.2进程、线程与信息共享1.3IPC对象的持续性1.4名字空间1.5fork、exec和exit对IPC对象的影响1.6出错处理:包裹函数1.7Unix标准1.8书中IPC例子索引表1.9小结习题第2章PosixIPC2.1概述2.2IPC名字2.3创建与打开IPC通道2.4IPC权限2.5小结习题第3章SystemVIPC3.1概述3.2key_t键和
- 大模型框架:vLLM
m0_37559973
大模型大模型通义千问Qwen
目录一、vLLM介绍二、安装vLLM2.1使用GPU进行安装2.2使用CPU进行安装2.3相关配置三、使用vLLM3.1离线推理3.2适配OpenAI-API的API服务一、vLLM介绍vLLM是伯克利大学LMSYS组织开源的大语言模型高速推理框架。它利用了全新的注意力算法「PagedAttention」,提供易用、快速、便宜的LLM服务。二、安装vLLM2.1使用GPU进行安装vLLM是一个Py
- Swift基础语法学习
中古传奇
swiftc++面试java
Swift基础语法学习0前言--Swift特点优势(忽悠点)1环境搭建1.1Xcode安装1.2离线安装踩坑指南2Swift语言2.1基本数据类型2.1.1申明常量和变量2.1.2整数类型2.1.3浮点数2.1.4布尔值2.1.5元组2.1.6可选类型2.1.7错误处理3断言和先决条件3.1断言和先决条件调试代码的好处3.2使用断言进行调试3.3强制执行先决条件3.4基本运算符时间:2021-22
- 微信小程序中组件封装与全局调用技巧
人工智能的苟富贵
前端小程序微信小程序小程序
文章目录前言一、组件传参方式1.1直接在组件标签上传参1.2调用组件内部方法传参1.3通过事件传参1.4通过回调函数传参二、组件封装与调用方式1.基础组件封装2.高级组件封装三、全局组件的封装与调用3.1.通过App()全局调用组件四、动态组件的加载与按需渲染五、不同传参方式的优缺点分析六、总结前言微信小程序的开发,离不开组件化思维。通过封装自定义组件,我们能够极大地提升开发效率、增强代码复用性。
- Websocket及三次握手/四次挥手
小童不学前端
网络通信websocket网络协议网络
Websocket-实时通信文章目录前言一、目前可实现实时通信的方式1、轮询(polling)2、长轮询(longpolling)3、Websocket3.1、WebSocket心跳机制3.2、WebSocket工作原理3.3、Websocket优点3.4、HTTP和Websocket关系二、HTTP协议-TCP三次握手、四次挥手1、TCP和TCP连接2、HTTP和TCP关系3、关于TCP连接的常
- 解线性方程组
qiuwanchi
package gaodai.matrix;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Test {
public static void main(String[] args) {
Scanner scanner = new Sc
- 在mysql内部存储代码
annan211
性能mysql存储过程触发器
在mysql内部存储代码
在mysql内部存储代码,既有优点也有缺点,而且有人倡导有人反对。
先看优点:
1 她在服务器内部执行,离数据最近,另外在服务器上执行还可以节省带宽和网络延迟。
2 这是一种代码重用。可以方便的统一业务规则,保证某些行为的一致性,所以也可以提供一定的安全性。
3 可以简化代码的维护和版本更新。
4 可以帮助提升安全,比如提供更细
- Android使用Asynchronous Http Client完成登录保存cookie的问题
hotsunshine
android
Asynchronous Http Client是android中非常好的异步请求工具
除了异步之外还有很多封装比如json的处理,cookie的处理
引用
Persistent Cookie Storage with PersistentCookieStore
This library also includes a PersistentCookieStore whi
- java面试题
Array_06
java面试
java面试题
第一,谈谈final, finally, finalize的区别。
final-修饰符(关键字)如果一个类被声明为final,意味着它不能再派生出新的子类,不能作为父类被继承。因此一个类不能既被声明为 abstract的,又被声明为final的。将变量或方法声明为final,可以保证它们在使用中不被改变。被声明为final的变量必须在声明时给定初值,而在以后的引用中只能
- 网站加速
oloz
网站加速
前序:本人菜鸟,此文研究总结来源于互联网上的资料,大牛请勿喷!本人虚心学习,多指教.
1、减小网页体积的大小,尽量采用div+css模式,尽量避免复杂的页面结构,能简约就简约。
2、采用Gzip对网页进行压缩;
GZIP最早由Jean-loup Gailly和Mark Adler创建,用于UNⅨ系统的文件压缩。我们在Linux中经常会用到后缀为.gz
- 正确书写单例模式
随意而生
java 设计模式 单例
单例模式算是设计模式中最容易理解,也是最容易手写代码的模式了吧。但是其中的坑却不少,所以也常作为面试题来考。本文主要对几种单例写法的整理,并分析其优缺点。很多都是一些老生常谈的问题,但如果你不知道如何创建一个线程安全的单例,不知道什么是双检锁,那这篇文章可能会帮助到你。
懒汉式,线程不安全
当被问到要实现一个单例模式时,很多人的第一反应是写出如下的代码,包括教科书上也是这样
- 单例模式
香水浓
java
懒汉 调用getInstance方法时实例化
public class Singleton {
private static Singleton instance;
private Singleton() {}
public static synchronized Singleton getInstance() {
if(null == ins
- 安装Apache问题:系统找不到指定的文件 No installed service named "Apache2"
AdyZhang
apachehttp server
安装Apache问题:系统找不到指定的文件 No installed service named "Apache2"
每次到这一步都很小心防它的端口冲突问题,结果,特意留出来的80端口就是不能用,烦。
解决方法确保几处:
1、停止IIS启动
2、把端口80改成其它 (譬如90,800,,,什么数字都好)
3、防火墙(关掉试试)
在运行处输入 cmd 回车,转到apa
- 如何在android 文件选择器中选择多个图片或者视频?
aijuans
android
我的android app有这样的需求,在进行照片和视频上传的时候,需要一次性的从照片/视频库选择多条进行上传
但是android原生态的sdk中,只能一个一个的进行选择和上传。
我想知道是否有其他的android上传库可以解决这个问题,提供一个多选的功能,可以使checkbox之类的,一次选择多个 处理方法
官方的图片选择器(但是不支持所有版本的androi,只支持API Level
- mysql中查询生日提醒的日期相关的sql
baalwolf
mysql
SELECT sysid,user_name,birthday,listid,userhead_50,CONCAT(YEAR(CURDATE()),DATE_FORMAT(birthday,'-%m-%d')),CURDATE(), dayofyear( CONCAT(YEAR(CURDATE()),DATE_FORMAT(birthday,'-%m-%d')))-dayofyear(
- MongoDB索引文件破坏后导致查询错误的问题
BigBird2012
mongodb
问题描述:
MongoDB在非正常情况下关闭时,可能会导致索引文件破坏,造成数据在更新时没有反映到索引上。
解决方案:
使用脚本,重建MongoDB所有表的索引。
var names = db.getCollectionNames();
for( var i in names ){
var name = names[i];
print(name);
- Javascript Promise
bijian1013
JavaScriptPromise
Parse JavaScript SDK现在提供了支持大多数异步方法的兼容jquery的Promises模式,那么这意味着什么呢,读完下文你就了解了。
一.认识Promises
“Promises”代表着在javascript程序里下一个伟大的范式,但是理解他们为什么如此伟大不是件简
- [Zookeeper学习笔记九]Zookeeper源代码分析之Zookeeper构造过程
bit1129
zookeeper
Zookeeper重载了几个构造函数,其中构造者可以提供参数最多,可定制性最多的构造函数是
public ZooKeeper(String connectString, int sessionTimeout, Watcher watcher, long sessionId, byte[] sessionPasswd, boolea
- 【Java命令三】jstack
bit1129
jstack
jstack是用于获得当前运行的Java程序所有的线程的运行情况(thread dump),不同于jmap用于获得memory dump
[hadoop@hadoop sbin]$ jstack
Usage:
jstack [-l] <pid>
(to connect to running process)
jstack -F
- jboss 5.1启停脚本 动静分离部署
ronin47
以前启动jboss,往各种xml配置文件,现只要运行一句脚本即可。start nohup sh /**/run.sh -c servicename -b ip -g clustername -u broatcast jboss.messaging.ServerPeerID=int -Djboss.service.binding.set=p
- UI之如何打磨设计能力?
brotherlamp
UIui教程ui自学ui资料ui视频
在越来越拥挤的初创企业世界里,视觉设计的重要性往往可以与杀手级用户体验比肩。在许多情况下,尤其对于 Web 初创企业而言,这两者都是不可或缺的。前不久我们在《右脑革命:别学编程了,学艺术吧》中也曾发出过重视设计的呼吁。如何才能提高初创企业的设计能力呢?以下是 9 位创始人的体会。
1.找到自己的方式
如果你是设计师,要想提高技能可以去设计博客和展示好设计的网站如D-lists或
- 三色旗算法
bylijinnan
java算法
import java.util.Arrays;
/**
问题:
假设有一条绳子,上面有红、白、蓝三种颜色的旗子,起初绳子上的旗子颜色并没有顺序,
您希望将之分类,并排列为蓝、白、红的顺序,要如何移动次数才会最少,注意您只能在绳
子上进行这个动作,而且一次只能调换两个旗子。
网上的解法大多类似:
在一条绳子上移动,在程式中也就意味只能使用一个阵列,而不使用其它的阵列来
- 警告:No configuration found for the specified action: \'s
chiangfai
configuration
1.index.jsp页面form标签未指定namespace属性。
<!--index.jsp代码-->
<%@taglib prefix="s" uri="/struts-tags"%>
...
<s:form action="submit" method="post"&g
- redis -- hash_max_zipmap_entries设置过大有问题
chenchao051
redishash
使用redis时为了使用hash追求更高的内存使用率,我们一般都用hash结构,并且有时候会把hash_max_zipmap_entries这个值设置的很大,很多资料也推荐设置到1000,默认设置为了512,但是这里有个坑
#define ZIPMAP_BIGLEN 254
#define ZIPMAP_END 255
/* Return th
- select into outfile access deny问题
daizj
mysqltxt导出数据到文件
本文转自:http://hatemysql.com/2010/06/29/select-into-outfile-access-deny%E9%97%AE%E9%A2%98/
为应用建立了rnd的帐号,专门为他们查询线上数据库用的,当然,只有他们上了生产网络以后才能连上数据库,安全方面我们还是很注意的,呵呵。
授权的语句如下:
grant select on armory.* to rn
- phpexcel导出excel表简单入门示例
dcj3sjt126com
PHPExcelphpexcel
<?php
error_reporting(E_ALL);
ini_set('display_errors', TRUE);
ini_set('display_startup_errors', TRUE);
if (PHP_SAPI == 'cli')
die('This example should only be run from a Web Brows
- 美国电影超短200句
dcj3sjt126com
电影
1. I see. 我明白了。2. I quit! 我不干了!3. Let go! 放手!4. Me too. 我也是。5. My god! 天哪!6. No way! 不行!7. Come on. 来吧(赶快)8. Hold on. 等一等。9. I agree。 我同意。10. Not bad. 还不错。11. Not yet. 还没。12. See you. 再见。13. Shut up!
- Java访问远程服务
dyy_gusi
httpclientwebservicegetpost
随着webService的崛起,我们开始中会越来越多的使用到访问远程webService服务。当然对于不同的webService框架一般都有自己的client包供使用,但是如果使用webService框架自己的client包,那么必然需要在自己的代码中引入它的包,如果同时调运了多个不同框架的webService,那么就需要同时引入多个不同的clien
- Maven的settings.xml配置
geeksun
settings.xml
settings.xml是Maven的配置文件,下面解释一下其中的配置含义:
settings.xml存在于两个地方:
1.安装的地方:$M2_HOME/conf/settings.xml
2.用户的目录:${user.home}/.m2/settings.xml
前者又被叫做全局配置,后者被称为用户配置。如果两者都存在,它们的内容将被合并,并且用户范围的settings.xml优先。
- ubuntu的init与系统服务设置
hongtoushizi
ubuntu
转载自:
http://iysm.net/?p=178 init
Init是位于/sbin/init的一个程序,它是在linux下,在系统启动过程中,初始化所有的设备驱动程序和数据结构等之后,由内核启动的一个用户级程序,并由此init程序进而完成系统的启动过程。
ubuntu与传统的linux略有不同,使用upstart完成系统的启动,但表面上仍维持init程序的形式。
运行
- 跟我学Nginx+Lua开发目录贴
jinnianshilongnian
nginxlua
使用Nginx+Lua开发近一年的时间,学习和实践了一些Nginx+Lua开发的架构,为了让更多人使用Nginx+Lua架构开发,利用春节期间总结了一份基本的学习教程,希望对大家有用。也欢迎谈探讨学习一些经验。
目录
第一章 安装Nginx+Lua开发环境
第二章 Nginx+Lua开发入门
第三章 Redis/SSDB+Twemproxy安装与使用
第四章 L
- php位运算符注意事项
home198979
位运算PHP&
$a = $b = $c = 0;
$a & $b = 1;
$b | $c = 1
问a,b,c最终为多少?
当看到这题时,我犯了一个低级错误,误 以为位运算符会改变变量的值。所以得出结果是1 1 0
但是位运算符是不会改变变量的值的,例如:
$a=1;$b=2;
$a&$b;
这样a,b的值不会有任何改变
- Linux shell数组建立和使用技巧
pda158
linux
1.数组定义 [chengmo@centos5 ~]$ a=(1 2 3 4 5) [chengmo@centos5 ~]$ echo $a 1 一对括号表示是数组,数组元素用“空格”符号分割开。
2.数组读取与赋值 得到长度: [chengmo@centos5 ~]$ echo ${#a[@]} 5 用${#数组名[@或
- hotspot源码(JDK7)
ol_beta
javaHotSpotjvm
源码结构图,方便理解:
├─agent Serviceab
- Oracle基本事务和ForAll执行批量DML练习
vipbooks
oraclesql
基本事务的使用:
从账户一的余额中转100到账户二的余额中去,如果账户二不存在或账户一中的余额不足100则整笔交易回滚
select * from account;
-- 创建一张账户表
create table account(
-- 账户ID
id number(3) not null,
-- 账户名称
nam