javascript实现KMP算法

假设

• 源字符串source为abcdabceedabcdabcdee，长度为m。
• 要匹配字符串match为abcdabcd，长度为n。

1.一般的子字符串查找方法

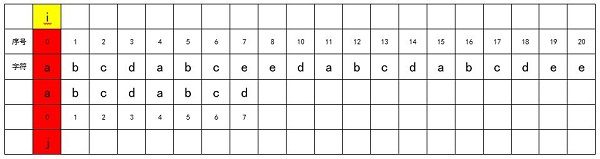
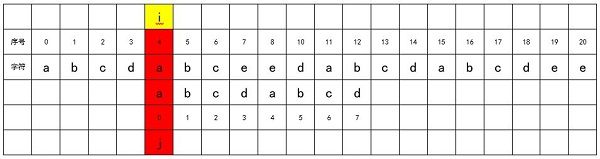
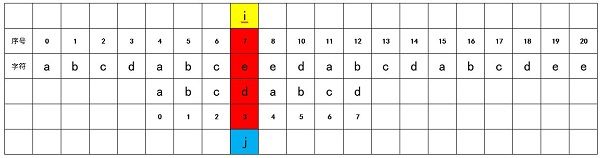
我们用i进行源字符串的索引，用j来对要匹配字符串match进行索引。我们从头部开始进行匹配，即i = 0，j = 0。source[0] == match[0],匹配成功，因此对j进行加1，即j = 1，继续匹配下一位。

source[1] == match[1],匹配成功，因此对j进行加1，即j = 2，继续匹配下一位。

source[2] == match[2],匹配成功，因此对j进行加1，即j = 3，继续匹配下一位。

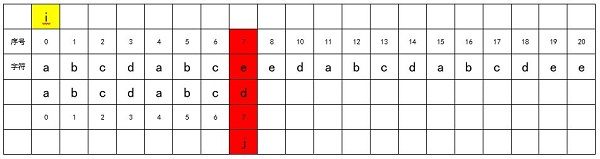
直到j = 7，出现了不匹配的情况，因此整个匹配过程被中断。

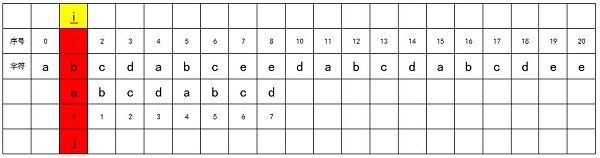
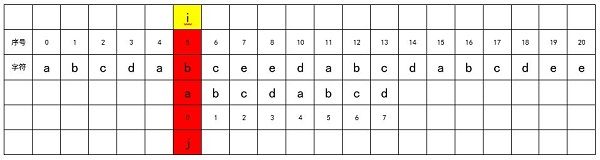
我们对i进行加1，即i = 1，将j归0，从match字符串的头部重新开始匹配，如下图所示：

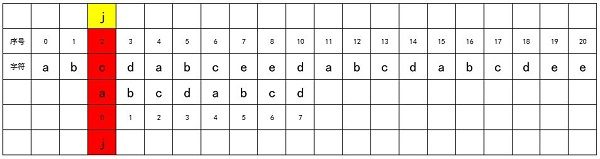
匹配不成功，对i进行加1，即i = 2，将j归0，从match字符串的头部重新开始匹配，如下图所示：

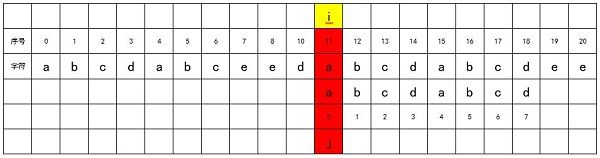
直到i = 4时，source[4] == match[0]，开始进行新一轮匹配过程。

当j = 3，出现了不匹配的情况：

因此和之前一样，对i进行加1，将j归0，重新开始匹配。

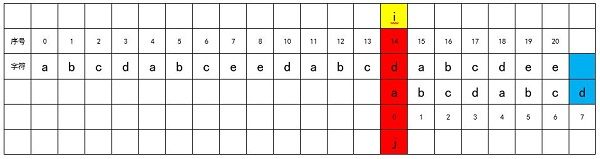
直到i = 11 时，开始进行新一轮匹配。

直到j = 18，完全匹配，此时j等于match字符串的长度，表明完全匹配。

之后，查找下一个匹配的位置，即对i加1，将j归0。

直到i大于source字符串的长度m减去match字符串的长度n，即i > m – n，结束整个查找过程。

我们发现这种匹配方式效率非常低，时间复杂度为O(m*n)。

2.KMP

KMP算法主要是根据match的特征优化i的调整步进。不需要再每次匹配不成功后对j进行归0，并对i进行加1。如下图所示，在i = 0，j = 7，出现了不匹配的情况：

我们分析match字符串可以发现：子串match[0]到match[2]与子串match[4]到match[6]完全一样。因此，我们直接调整j，从match[3]的位置和当前的source[7]进行比较，不需要从source[1]的位置重新进行匹配。

3.NEXT数组计算

next数组和待匹配字符串数组长度一样，用于保存当前位置的字符作为结束与头部能够匹配的长度值减1，减1的原因就是便于数组索引，因为数组索引是从0开始的。

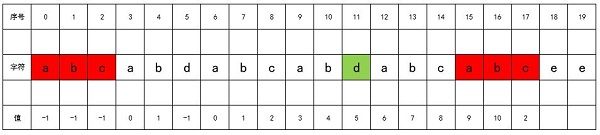
如下图所示，为待匹配字符串match，第一行为字符在数组中的索引，第二行为字符串，第三行为next数组的值，即能够匹配的长度值减1。

待匹配字符串

• 从0开始，因为第一个字符之前没有字符，所以长度为0，减1之后为-1。
• 同理，以第二个字符作为结束的字符串只能有ab或者b，因为它不能和自己本身进行匹配，所以长度为0，减1之后为-1。
• 直到第四个字符，它可以和第一个字符匹配，因此长度为1，减1之后为0。
• 第五个和第四个结合在一起，可以和第一个字符和第二个字符结合体匹配，所以长度为2，减1后为1。
• 第六个也是如此。
• 接下来应该是第七个和第三个进行匹配，但是两个不相等，此时我们就要思考如何计算，而next数组计算的难点也就在于此。

我们需要采用递归的方式，因为第七个字符和前面紧挨着它的某一部分字符串拼接的字符可能和头部匹配，比如str[15]到str[18]与str[0]到str[3]，我们来具体看一看。

当i = 18时，我们会发现str[7] !== str[18]，此时我们不能马上下结论说要从头开始匹配，即从序号为0的位置开始，那样将意味着next[18] = -1或者0。由于str[18]之前的子串中会有一部分和前面匹配，比如此处的str[15]到str[17]“abc”和str[0]到str[2]“abc”相同。所以，正确的匹配应该是下面这种情况：

正是因为在前面字符串中存在着子串，所以我们需要递归对子序列进行判断。也就说我们需要判断str[18]是否可以和前面紧挨着的一部分字符串匹配到开始的字符串。也就说我们要对str[0]到str[6]之间字符串进行检查，看以str[6]为结束的字符串是否会和头部匹配。

next[6]等于2，则说明以str[6]为结束的字符串与头部匹配的长度为3，即str[4]到str[6]与str[0]到str[2]相同。因此如果str[18]和str[3]相同，那么说明str[15]到str[17]（str[15]到str[17]和str[4]到str[6]肯定相同，因为之前的匹配过程已经匹配过了，不然也不会到这一步）加上str[18]应该str[0]到str[3]这段字符串一致。这样一来的话，next[18]应该等于3。

如果str[18]和str[3]不同，说明还要进行递归查询，如下所示：

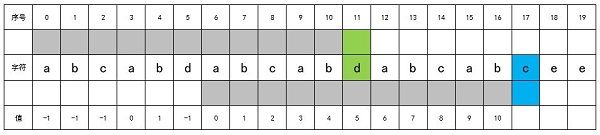
当计算到str[11]和str[12]的时候，因为不相同，所以要进行递归查找，即str[17]之前的某部分子串是否可以和str[17]结合在一起，与头部开始匹配，究竟从哪开始？这个我们无法确定，我们只有不断的去递归查找。
第一次我们j = next[j]，此时j = 10，所以j = next[10]，即j = 4。那么我们比较str[4+1]和str[17]，发现两者不相等。所以我们需要进行再次递归，递归范围在str[0]到str[4]，也就是判断以str[4]为后缀结束字符的字符串可以和头部匹配多长。

第二次，我们继续令j = next[j]，此时j = 4，所以j = next[4]，即j = 1。那么我们比较str[1+1]和str[17]，发现两者相等，那么递归结束，我们计算得到next[17] = j + 1，即j = 2。如下图所示：

代码实现：

function calcNext(str){

  let next = [-1],
      len = str.length,
      i = 1,
      j = -1;

  for (i = 1; i < len; i++) {

    while (str[i] !== str[j+1] && j > -1) {
      j = next[j]; // 递归
    }

    if (str[j+1] === str[i]) {
      j = j + 1;
    }
    // else j = -1
    // 此时j已经等于-1，因此可以省略此段代码

    next[i] = j;

  }

  return next;
}

4.完整实现代码

(function(){

  // 计算next数组
  function calcNext(str){

    let next = [-1],
        len = str.length,
        i = 1,
        j = -1;

    for (i = 1; i < len; i++) {

      while (str[i] !== str[j+1] && j > -1) {
        j = next[j];
      }

      if (str[j+1] === str[i]) {
        j = j + 1;
      }

      next[i] = j;

    }

    return next;
  }

  // source 源字符串
  // match 要匹配的字符串
  // res 保存匹配位置的数组
  function search(source, match){
    let next = calcNext(match),
        m = source.length,
        n = match.length,
        i = 0,
        j = 0,
        res = [];

    while (i < m-n) {
      if (source[i] === match[j]) {
        i++;
        j++;

        if (j === n) {
          res.push(i-n);
          j = next[j-1] + 1;
        }
      } else {
        if (j === 0) {
          i++;
        } else {
          j = next[j-1] + 1;
        }
      }
    }

    return res;
  }

  let source = '21231212121231231231231232234121212312312312331212123',
      match = '12123123123123';

  let res = search(source, match);
  console.log(res);

})();

喜欢的话，点个赞！