R语言之生信⑤TCGA生存分析2

目录

R语言之生信①差异基因分析1

R语言之生信②差异基因分析2

R语言之生信③差异基因分析3

R语言之生信④TCGA生存分析1

R语言之生信⑤TCGA生存分析2

R语言之生信⑥TCGA生存分析3

R语言之生信⑦Cox比例风险模型(单因素)

=========================================================

正文

接上文，Kaplan-Meier曲线有助于可视化两个分类组之间的生存差异，当你设置参数pval = TRUE时，可以获得的对数秩检验值有助于探讨不同组之间的生存率是否存在差异。 但这并不能很好地评估连续性定量变量的对生存的影响。比如你的某一个node属性取值范围是0-33，这将导致生存曲线图上出现33条生存曲线。如果遇到分组过多或者想要评估多个变量如何协同以影响生存。 例如，比如当希望同时检查种族和社会经济状况对生存的影响时就可能需要换种生存分析方法。

Cox PH回归可以评估分类变量和连续变量的影响，并且可以一次模拟多个变量的影响。 coxph（）函数使用与lm（），glm（）等相同的语法。使用Surv（）创建的响应变量位于公式的左侧，用〜指定。

让我们使用常见的肺癌数据并对性别进行Cox回归分析。

> fit <- coxph(Surv(time, status)~sex, data=lung)
> fit
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)

      coef exp(coef) se(coef)     z      p
sex -0.531     0.588    0.167 -3.18 0.0015

Likelihood ratio test=10.6  on 1 df, p=0.00111
n= 228, number of events= 165 

exp（coef）列是风险比 - 该变量对危险率的乘法效应（对于该变量的每个单位增加）。因此，对于像性别这样的分类变量，从男性到女性，死亡风险降低约40％。如果翻转coef的正负，比如exp（0.531），您可以将其解释为从女性到男性，死亡危险性增加1.7倍，或者男性死亡率约为每单位时间内女性1.7倍（女性死亡率为每单位时间男性的0.588倍）。

简单起见可以用下列来解释：

• HR = 1：无效
• HR> 1：危险增加
• HR <1：减少危害（保护性）
  下一步让我们创建一个模型来分析数据集中的所有变量！ 这向我们展示了所有变量在一起考虑时如何影响生存。比如其中有一些变量是非常强大的预测因子（性别，ECOG评分）。

> fit <- coxph(Surv(time, status)~sex+age+ph.ecog+ph.karno+pat.karno+meal.cal+wt.loss, 
+              data=lung)
> fit
Call:
coxph(formula = Surv(time, status) ~ sex + age + ph.ecog + ph.karno + 
    pat.karno + meal.cal + wt.loss, data = lung)

               coef exp(coef)  se(coef)     z      p
sex       -5.51e-01  5.76e-01  2.01e-01 -2.74 0.0061
age        1.06e-02  1.01e+00  1.16e-02  0.92 0.3591
ph.ecog    7.34e-01  2.08e+00  2.23e-01  3.29 0.0010
ph.karno   2.25e-02  1.02e+00  1.12e-02  2.00 0.0457
pat.karno -1.24e-02  9.88e-01  8.05e-03 -1.54 0.1232
meal.cal   3.33e-05  1.00e+00  2.60e-04  0.13 0.8979
wt.loss   -1.43e-02  9.86e-01  7.77e-03 -1.84 0.0652

Likelihood ratio test=28.3  on 7 df, p=0.000192
n= 168, number of events= 121 
   (60 observations deleted due to missingness)

下一步，我们尝试在肺数据集上基于年龄属性创建一个分类变量，其中以0,62（平均值）和Inf（无限大）为截断值。 基于截断值我们可以添加labels =选项来标记我们创建的分组，例如，'yong'和'old'。 最后，我们可以将结果分配给肺数据集中的新对象。

mean(lung$age)
hist(lung$age)
ggplot(lung, aes(age)) + geom_histogram(bins=20)

cut(lung$age, breaks=c(0, 62, Inf))
cut(lung$age, breaks=c(0, 62, Inf), labels=c("young", "old"))

# the base r way:
lung$agecat <- cut(lung$age, breaks=c(0, 62, Inf), labels=c("young", "old"))

# or the dplyr way:
lung <- lung %>% 
  mutate(agecat=cut(age, breaks=c(0, 62, Inf), labels=c("young", "old")))

head(lung)
> head(lung)
  inst time status age sex ph.ecog ph.karno pat.karno meal.cal
1    3  306      2  74   1       1       90       100     1175
2    3  455      2  68   1       0       90        90     1225
3    3 1010      1  56   1       0       90        90       NA
4    5  210      2  57   1       1       90        60     1150
5    1  883      2  60   1       0      100        90       NA
6   12 1022      1  74   1       1       50        80      513
  wt.loss agecat
1      NA    old
2      15    old
3      15  young
4      11  young
5       0  young
6       0    old

现在，通过截断值我们将age属性截断成“老”和“年轻”两类患者的曲线，同时探讨两者的生存曲线是否存在一些差异，老年患者的生存几率略差。 但是如下图所示p值 = 0.39时，这说明62岁以下和62岁以下人群的生存率差异不显着。

ggsurvplot(survfit(Surv(time, status)~agecat, data=lung), pval=TRUE)

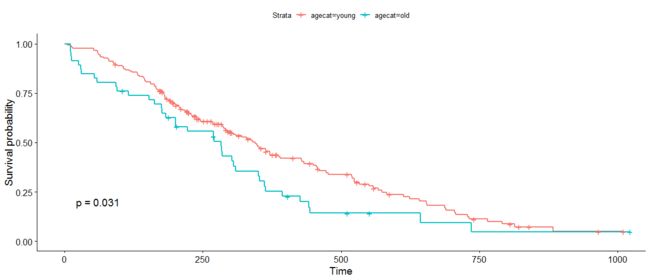
但是，如果我们选择一个不同的切点，比如70岁，这大致是年龄分布的上四分位数的截止值（参见？分位数）。 结果现在略显重要！

# the base r way:
lung$agecat <- cut(lung$age, breaks=c(0, 70, Inf), labels=c("young", "old"))
# or the dplyr way:
lung <- lung %>% 
  mutate(agecat=cut(age, breaks=c(0, 70, Inf), labels=c("young", "old")))
# plot!
ggsurvplot(survfit(Surv(time, status)~agecat, data=lung), pval=TRUE)

请记住，Cox回归是分析连续变量在其分布范围内，其中Kaplan-Meier图上的对数秩检验值可以根据您对连续变量的截断值分组而改变。 这两种生存分析方法以不同的方式回答了一个类似的问题：回归模型是在问“年龄对生存的影响是什么？”，而生存表法回答的问题是，“组与组之间存在生存差异吗？ 比如在那些不到70岁的人群和70岁以上的人群？“