PCA只对符合高斯分布的样本点比较有效
ICA对于高斯分布的样本点无效,对于其他分布的有效。
回顾我们之前介绍的《模型选择和规则化》,里面谈到的特征选择的问题。但在那篇中要剔除的特征主要是和类标签无关的特征。比如“学生的名字”就和他的“成绩”无关,使用的是互信息的方法。
这里的,是想把与类标签有关的,但是相似的特征组成一个好的。比如在语义分析中,learn和study是类似的,出现的频率也类似,能不能合为一个特征呢?
而这里的特征很多是和类标签有关的,但里面存在噪声或者冗余。在这种情况下,需要一种特征降维的方法来减少特征数,减少噪音和冗余,减少过度拟合的可能性。
PCA的思想是将n维特征映射到k维上(k
一、PCA步骤
1、数据处理,求均值,相减,替换,求方差,替换
这里第一步数据处理的意义,就是想让投影后的样例之间,均值为 0。
第二步数据处理的意义就是归一化了,比如样例中,一个特征是汽车速度,一个特征是汽车座位数,显然第二个方差比第一个小。这样协方差矩阵中的值会受到影响。
所以需要归一化。
2、求特征协方差矩阵
3、求协方差矩阵的特征值和特征向量
4、将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
上面的如果k=1,那么只会留下这里的水平轴,轴上是所有点在该轴的投影。
5、将样本点投影到选取的特征向量上。
假设样例数为m,特征数为n,减去均值后的样本矩阵为DataAdjust(mn),协方差矩阵是nn,选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为
----------------------------------------------------------------------------------------
这样,就将原始样例的n维特征变成了k维,这k维就是原始特征在k维上的投影。
----------------------------------------------------------------------------------------
理论基础
参考Jerrylead图。
在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。如前面的图,样本在横轴上的投影方差较大,在纵轴上的投影方差较小,那么认为纵轴上的投影是由噪声引起的。
因此我们认为,最好的k维特征是将n维样本点转换为k维后,每一维上的样本方差都很大。
我们要找到一个最佳的u,使得样例的特征x在u上投影后,方差最大。经过来回化简(参考讲义),我们得到
λ即作为特征值,又作为特征点投影后的方差。
根据上面,我们想要得到一个最佳的u,使得投影后的方差最大。那么也就是说,上式中,λ最大时(也就是方差最大时)的u即为所求。
此时,u是协方差矩阵的特征值λ对应的特征向量。解答完毕。
------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------
二、ICA步骤
1、问题 经典的鸡尾酒宴会问题
s是人发出的信号,x是得到的一组数据,A是一个未知的混合矩阵,用来叠加信号s。于是有
这里x(i)的每个分量都是由s(i)的分量线性表示。A和s都是未知的,x是已知的,我们要想办法根据x来推出s。这个过程也称作为盲信号分离。
先表达出每个信号源s(i)(即我们最终想要得到的每个人说话的声音):
2、ICA的不确定性
从上面可知,我们只知道一个x,其余两个变量w和s都是不知道的。在没有先验知识的情况下,是无法同时确定这两个相关参数的。
还有,在已知先验知识的情况下,如果信号服从高斯分布,根据推断,也是不能确定原信号的。
那么,我们就给s假设出一个合理的分布,这样,就可以求得p(x)
知道了p(s),x也已经有,和概率有关,在给定采样后的训练样本以后,做对数似然估计,可得到
对W求导,就可得到w的迭代公式。
迭代求出W后,便可以用s=Wx来还原出原始信号。
------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------
ICA和PCA的对比
PCA主成分分析==>主要的k个特征
ICA独立成分分析==>独立的信号
ICA是盲信号分析领域的一个强有力方法,也是求非高斯分布数据隐含因子的方法。
从之前我们熟悉的样本-特征角度看,我们使用ICA的前提条件是,认为样本数据由独立非高斯分布的隐含因子产生,隐含因子个数等于特征数,我们要求的是隐含因子。
而PCA认为特征是由k个正交的特征(也可看作是隐含因子)生成的,我们要求的是数据在新特征上的投影。
同是因子分析,一个用来更适合用来还原信号(因为信号比较有规律,经常不是高斯分布的),一个更适合用来降维(用那么多特征干嘛,k个正交的即可)。有时候也需要组合两者一起使用。
3、线性判别分析(LDA)
PCA降维没有将类别标签考虑进去,属于无监督的。
而LDA降维,将类别标签考虑了进去,使得投影后的不同类样本点越分开越好(不同类的中心点距离越大越好),同类的越聚集越好(散列度越小越好)。
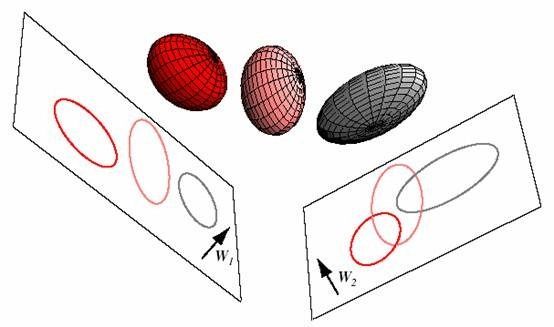
LDA效果:将3维空间上的球体样本点投影到二维上,W1相比W2能够获得更好的分离效果。
PCA与LDA的降维对比
PCA选择样本点投影具有最大方差的方向,LDA选择分类性能最好的方向。