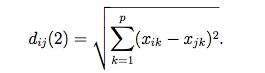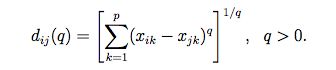各位小伙伴们大家好,这几天我在学习聚类分析这个统计方法,所以希望通过这个文章来概括下自己所学的知识,并且希望大家可以指出不足
1:什么是聚类分析?
聚类分析(cluster analysis)是一种将数据所研究的对象进行分类的统计方法,像聚类方法这样的一类方法有个共同的特点:事先不知道类别的个数和结构,据以进行分析的数据是对象之间的相似性(similarity)和相异性(dissimilarity)的数据.将这些相似(相异)的数据可以看成是对象与对象之间的”距离”远近的一种度量,将距离近的对象看做一类,不同类之间的对象距离较远,这个可以看作为聚类分析方法的一个共同的思路.
聚类分析可以根据分类对象的不同分为Q类型聚类分析和R类型聚类分析.
Q类型可以看做为对于样本的聚类,R类型可以看作为对于变量进行聚类分析.
2:距离和相似系数
其实个人觉得,聚类分析本质上就是研究样本和变量的聚类的一个过程,尽管我们在聚类的时候使用的方法有很多,但是这样的方法的选择往往都和变量的类型有关系,因为数据来源和测量方法的不同,我们可以把变量大致分为两类:
1:定量的变量:比如说我们的长度重量,人口,速度等,这些变量都是由具体的特征数值所构成,很多都是用真实的测量计数而来
2:定性变量:这样的量并非只有数量上的变化,但是往往有一些性质上的差异,比如说成绩的名次,性别,产品的型号等等.
1:距离:
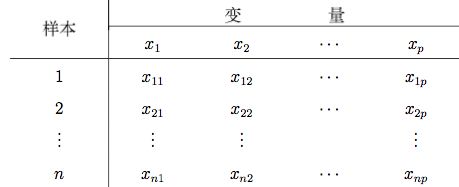
现在设X(ik)为第i个样本的第K个指标,数据矩阵如图所示:
每一个样本都具有P个变量,现在我们把每个样本看成为一个点,这n个样本就可以看作为n个点,第i个样本与第j个样本之间的距离记作为d(ij),在聚类的过程中,个人倾向于距离较近的点归为一类,距离较远的点归为不同的类.距离必须满足一下几个条件:
1:对于一切的i,j,d(ij)>=0;
2:d(ij)=0,当且仅当i,j个样本的各种变量相同;
3:dij=dji,对于一个i,j
4:dij<=dik+dkj,对于一切i,j,k
对于求距离的几种常用的方法:
1:求绝对值距离:
2:Euclide距离:
3:Minkowski距离:
这里我发现绝对值距离和Eucide距离是MinKowski距离的特例,要是各种变量的单位不同或者测量值范围相差很大时,不应该采用Minkowski距离,应该是先进行标准化数据处理,然后再用标准化数据进行计算.
4:chebyshev距离:
这个是minkowski距离中q趋向于无穷的时候的状况
以上的这几种都是丢定量变量的距离定义,还有几种定性的变量距离定义的方法,接下来打算用实例的时候再结合进行解释:
2:相似系数
聚类分析方法不仅用对样本进行分类,而且也可以用对变量进行分类,在对变量进行分类时,一般用相似系数来度量变量之间的相似程度:
现在我们设C(ij)表示Xi和Xj间的相关系数一般要求:
当C(ij)越接近于1,说明Xi和Xj之间的关系也就越亲切,如果C(ij)越接近0,则两者的关系也就越疏远.一般用求夹角余弦的方法,来求相似的系数.
3:一个实例:
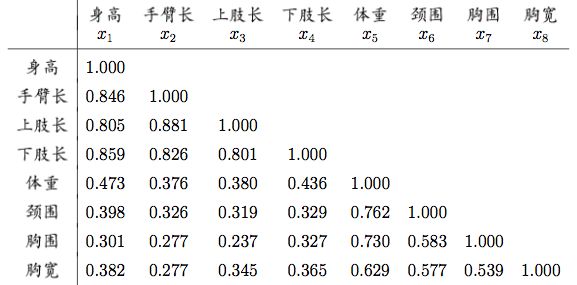
对305名女中学生测量8个相关的体型指标,相应的相关矩阵如下图所示,将相关系数看做相似系数,定义距离为:
现在使用最长距离法做系统分析:
现在解题的方法如下:
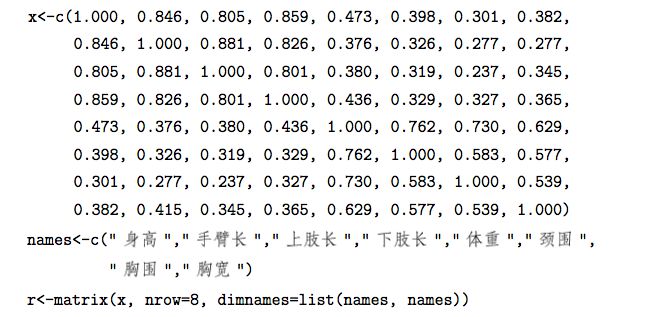
首先,我们先输入相应的相关系数矩阵,这里使用R语言来进行操作:
1:先输入相关的矩阵
然后做相关的系统聚类分析
这里边使用了一个新的函数as.dist(),其作用是将普通的矩阵转化为聚类分析所使用的距离结构
d<-as.dist(1-r);hc<-hclust(d);dend<-as.dendrogram(hc)
然后写一段小程序,在绘图命令中调用它,使谱系图变得更好看
最后一步,画出谱系图:
de <- dendrapply(dend,addE);plot(de,nodePar= nP)
所有的代码如图所示:
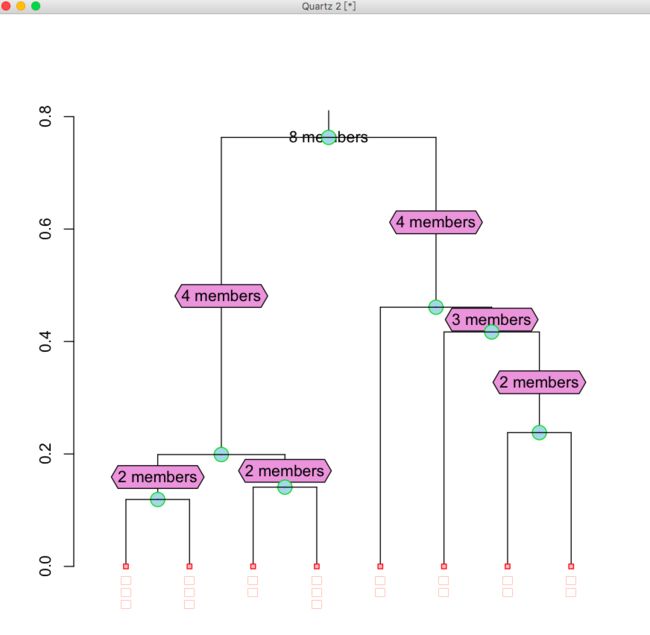
所得到的图形如图所示:
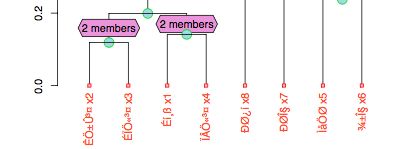
从这个图里我们可以看出,变量X2(手臂长)与X3(上肢长)首先合为一类,接下来是X1(身高)和X4(下肢长)合并为一了你,在合并就是讲得到的类合并为一个新类,后边的X5和X3合并,最后X7,X8合并为一类.
这个时候,肯定有很多的小伙伴们想,在聚类中类的个数应该怎么选择才是最适宜的,所以我想在下一篇文章中讲一讲我对于类的个数的确定以及系统聚类法的自己学习的一些经验.
PS:自己在学习中,曾经陷入到了深陷算法推理的迷局,往往花费大量时间,还得不到结果,但是我们并不是每个人都有数学天赋,并不是每个人都是数学家,这个时代更最看重的是我们的应用能力,我们只需要保证我们理解调用就好,所以我尽量减少算法推理过程,加强工具的使用过程,大家一起加油吧!