书本内容:见相册
preface
还记的我们上一篇说的Monte Carlo 维度诅咒吗
上一篇算是二维的例子吧,大家看了之后是否想着写一个一维的Monte Carlo模拟积分?(我想了,没写出来)
为什么要整这个嘞
光照渲染中多处涉及重积分,最终结果是要求取一个近似值,因而需要对其值进行数值估计,Monte Carlo方法就是一个较为理想的方案。
其实我们的光线追踪器不仅用了很多向量运算,还用了很多数值分析的知识,比如之前的背景用的是最简单的插值,柏林噪声纹理用的是三线性插值等
ready
你需要对以下知识有了解:
二重定积分
概率密度函数
反函数
Chapter 2:One Dimensional MC Integration
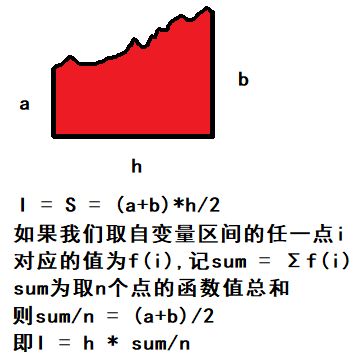
积分是用来求取面积或者体积的东东,常见形式为:I=∫x2 dx
假设积分区间为0->2,我们用计算机符号表示为I = area(x2,0,2)
那么我们来模拟以下这个积分
我们先来看一个普通的:
那么,我们就可以写代码了(程序2-1)
void MC_integration(double(*f)(double x), double low, double high) { size_t all = 1000000; double sum{ 0 }; for (int i = 0; i < all; ++i) { double x = 2 * rand01(); sum += x*x; } stds cout << "I = " << 2 * sum / all << stds endl; } int main() { MC_integration([](double x) {return x*x; }, 0, 2); }
正如我们所期望的,但上述方法也可以计算那些我们用解析法无法解决的积分,如被积函数为log(sin(x)。
在图形学中,我们经常有一些我们可以评估但不能明确写下来的函数,或者我们只能概率评估的函数。 事实上,前面两本书的光线追踪代码中的lerp函数,其实我们不知道在每个方向上看到的是什么颜色,但我们可以在任何给定的维度上统计估算它。
我 又想起来上本书刚刚写过的区域光照渲染图片,里面的黑色噪点真的把好精美的Cornell box 盒子给糟蹋了,那时因为我们对所有的东西做了统一的采样,而没有对光源进行足够的光源采样,所以我们可以对光源进行更多的随机采样,但是我们又需要控制这个比重,以防止过采样的发生,所以,如何控制这个比例,已达到更好的效果,这就需要引入一个非常重要的概念——重要性采样
但是在讲重要性采样之前,我们需要了解一些关于概率密度函数的东东
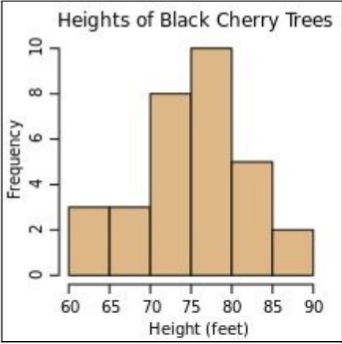
先看书上这张图
如果我们添加更多的tree,那么这张图的长条将会增高(变长),因为他们的数量更多了,如果Height轴细分为更多的小块,那么,每个长条的高度会降低(变短)。
离散密度函数与直方图的不同之处在于它将频率y轴归一化为分数或百分比。
而连续直方图中,我们将Height轴细分为无数个小块,那么,纵轴将不会是一个分数,因为所有小格对应的长条基本没有高度(每个小格代表的树高区间基本只有一棵树或者没有树,出现频率几乎为0)
所以对于密度函数,我们调整小格对应的影响因素,使得我们添加更多的小格时,长条不会太低
对于上述条形图,我们采取如下:
小格的高 = 树高介于H~H'的比例 / (H - H')
它将是很有用的! 我们可以将其解释为树高的统计预测器:
即:一个介于H~H'的随机树高的概率 = 小格的高 * (H - H')
如果我们需要知道多个小格对应的概率,那么加和即可
其实上述公式就构成了概率密度函数,即,面积代表着对应横坐标区间的概率,也就是上面的第二个公式
而概率密度函数就是一种连续的分数直方图,简称为pdf(probability density function)
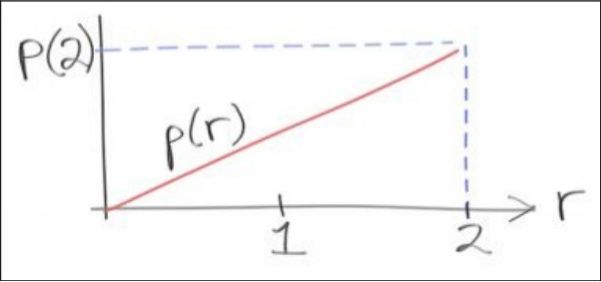
让我们来整一个pdf,或许会有更深入的理解。如果我想要一个0~2的随机数r它的出现概率和r自己成比例,我们将期望pdf为如下图像:
r位于(x0,x1)的概率为C*area(p(r),x0,x1),其中C为常量,为了简便,C一般取1
而area(p(r),0,2) = 1(概率密度函数的总面积就是总概率)
因为p(r)和r成比例,所以,设另一个常量C',则p(r) = C'r
故我们解积分:
1 = ∫0->2 C'r dr = C'r2/2|0->2 = 2C' =>C' = 1/2 公式2-1
所以 p(r) = r/2
我们如何用pdf p(r)生成一个随机数?为此我们需要更多的机器。不要担心这不会永远持续下去!(不会像上一篇最后那个程序,永无止境。。)
给一个随机数d = rand01(),我们知道我们写的rand01()产生的随机数对于0~1的每个浮点数的概率都是均匀一致的,我们需要找个函数f(d)得到我们想要的。假定e = f(d) = d2,这次将不再是一个均匀一致的pdf了,以前是的,之后我们讲(把此处记为pos1遗留问题)
我们为了观察这个函数还需要累积概率分布函数Cpdf(Cumulative probability distribution function)
记为P(x),则P(x) = area(p,-inf,x),几何意义就是从负无穷到x的累积概率和,也就是x左边部分的积分形成的面积
而且我们规定在没有定义的定义域内p(x) = 0,若采用pdf函数p(r) = r/2,那么,P(x)如下:
P(x) = 0, x < 0
P(x) = x2/4, 0 < x < 2
P(x) = 1, x > 2
当x∈(0,2),P(x) = ∫0->x p(r) dr = ∫0->x r/2 dr = x2/4
那么,x和r是什么关系?其实就是两个虚拟变量,类似于程序中的参数,如果我们把x调整为有效区间的中点,那么
P(1.0) = 1/4
这就是说基于我们的pdf概率密度函数p(r) = r/2的设定下产生一个小于1的随机数的概率为25%
这产生了一种巧妙的观察结果,这种观察结果是产生非均匀随机数的许多方法的基础。
我们想要一个函数f(),它满足:
当我们调用f(drand48())时,我们得到一个基于设定的Cpdf(x2/4)的一个返回值。 我们不知道那是什么,但我们知道当x为25%时应该小于1,而参数为75%应该高于1。 如果f()为增函数,那么我们期望f(0.25)= 1.0。
上面说了一堆,意思就是x和r无非就是函数参数,即P(1.0) = 0.25的时候,我们同样想得到一个函数f(),它满足f(0.25)=1.0
即:根据Cpdf得知随机数小于1.0的概率为0.25,而存在一个f(),使得以0.25为参数的时候能够得到那个1.0(即累积概率分布函数右端的边界线)
这可以推广到每个可能的输入
即:f(P(x)) = x
也就是说f(x) = P-1(x)
也就是P(x)的反函数。对于我们的目的而言,上述的意思就是:如果我们有了pdf函数p()和对应的Cpdf函数P(),我们为f()输入一个随机数,那么它就会给出我们想要的:
e = P-1(rand01())
对于我们的pdf函数p(x) = x/2,以及对应的P(x),我们需要计算P-1
即:如果我们有 y = x2/4
那么,x = sqrt(4y)
因此基于pdf,我们输入随机数,得到的就是
e = sqrt(4*rand01())
那么e∈(0,2),正如我们所期望的,我们输入一个0.25,它就返回一个1.0
到了这里,其实上面重复了很多废话,上面一大堆,表面上干了一个什么事情呢,用一个0~1的随机数映射0~2这个积分区间
我们想一下我们要做的是什么,模拟x的二次方曲线的积分,我们要用随机数模拟随机选取积分区间的值,而我们的积分区间就是0~2,
但是没必要这么麻烦啊,0~1随机数随机模拟0~2取值,直接2 * rand01()不就完啦,也就是程序2-1
不不不,它们有着天差地别,我们上述一顿操作是为了引入一个概念——Important Sample
我们通过设置pdf使得,对于积分区间的自变量取值有了权重比例,也就是说有些地方的采样要多一点,有些地方要少一点。
也就是:I = 1/n * Σ(F(xi)/pdf(xi))
由此可知,每个积分采样 Ii = 采样高度(函数值)/该采样点占的权重,所有的积分采样取均值,实现了不同采样点为整个积分做的贡献是不同的
constexpr double pdf(const double x) {return 0.5 * x; } void pdf1() { size_t all{ 100000 }; double sum{ 0. }; for (int i = 0; i < all; ++i) { double x = sqrt(4 * rand01()); sum += x*x / pdf(x); } stds cout << "I = " << sum / all << stds endl; }
我们来解释pos1处的遗留问题
之前的程序2-1所指的积分方案中,是均匀一致采样,即对于任意采样点同等对待
即,设p(x) = C
则公式2-1 写为
1 = ∫0->2 C dr = Cr|0->2 = 2C =>C = 1/2
即,开篇的方法中的pdf函数为p(x) = 1/2
所以程序2-1可以改写为:
constexpr double pdf(const double x) {return 0.5; } void pdf1() { size_t all{ 100000 }; double sum{ 0. }; for (int i = 0; i < all; ++i) { double x = 2 * rand01(); sum += x*x / pdf(x); } stds cout << "I = " << sum / all << stds endl; }
在important sample中我们觉得函数峰高的部分对于整个积分的贡献更多,低峰对于积分贡献不大,所以我们对于x2积分函数采取的pdf函数为x/2
其实,pdf应该采取的就是积分函数本身,在知道答案的情况下,我们采取如下pdf函数最佳:
p(x) = (3/8)x2
则P(x) = x3/8
P-1(x) = pow(8x,1/3)
则函数为:
constexpr double pdf(const double x) { return 3 * x * x / 8; } void pdf1() { size_t all{ 1 }; double sum{ 0. }; for (int i = 0; i < all; ++i) { double x = pow(8 * rand01(), 1. / 3); sum += x*x / pdf(x); } stds cout << "I = " << sum / all << stds endl; }
至此,所有的内容都已经阐述完毕
我们回顾一下,因为这个是光线追踪蒙特卡罗中的大部分概念
1. 你有一个被积函数f(x)的积分域【a,b】
2. 在域【a,b】中选择一个非零的pdf函数p()
3. 对所有的积分采样Ii = f(r)/p(r)取平均,pdf函数p(),随机数r
这总是会收敛到正确答案,p越接近f,收敛越快
感谢您的阅读,生活愉快~