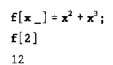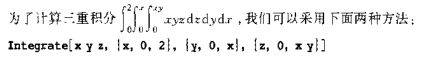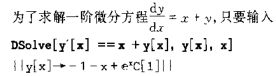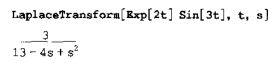作者:桂。
时间:2018-06-27 21:53:34
链接:https://www.cnblogs.com/xingshansi/p/9236502.html
前言
打算系统学习一些数学知识,容易碰到一些复杂数学的求导、积分,Mathmatica在这方面有优势,简单了解一下,打算后续运算主要借助它来完成。
软件来自北邮人论坛。 学习资料——主要参考:Mathmatica权威指南.pdf。
一、Mathmatica简介
Mathmatica更侧重数学运算,主要功能有:
1)符号运算【仅这一点就能省去多少草稿纸?】
- 初等数学
- 微积分
- 线性代数
- 解方程组
- ....
2)数值计算
- 求极值
- 插值与拟合
- 数值积分
- 线性代数
- 线性规划
- 概率统计
- ....
3)数据可视化
主要是数据的展示,初步来看,Mathmatica个人觉得比MATLAB优秀。
基本界面:
二、Mathmatica常用操作
以后需要经常使用该软件,先熟悉常用快捷键:
遇到一个新工具,自然会问到3个问题:
1)如何查找帮助文档?了解该点就学会了解决问题的方法。
2)常用快捷键? 该点提高操作效率。
3)是否支持模块化? 该点对于复杂模型尤其重要。
A-查找帮助文档
参考网页:http://www.wolfram.com/mathematica/new-in-10/symbolic-geometry/integrate-over-regions.html
输入指令,右键:帮助。
或选中指令,F1.
帮助里可以查找所选函数,例如高数::
选择高等数学计算:
B-常用快捷键
- shift enter:运行
- Crtl + N:新建笔记本
- Crtl + home/end:跳转
- Crtl + K,类似TAB,完整指令名
- Crtl + O:打开文件
- Crtl +shift + B: 检查括号平衡
- 停止:crtl + break
- 继续:F5 步进F10 步入F11 步出SHIFT+F11 中断F9 步出shift+CRTL+F9
- 清除变量:clear[var]
- 清屏:可关闭 + Crtl N的操作 /Crtl + A ,del
- 其他用到再补充,参考附件。
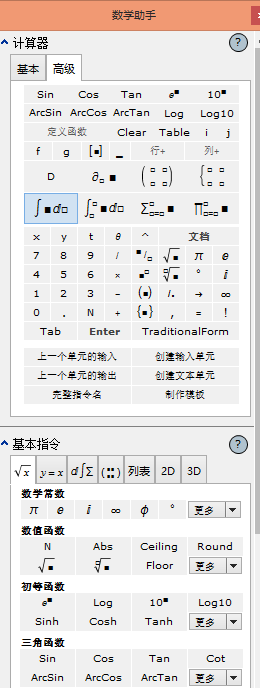
可借助面板——数学助手,类似mathtype敲打公式,自动转换为mathmatica指令:
其中包括公式中的特殊字符:
C-模块化
Crtl + N ,新建*.nb格式的文件。
三、常用数学运算
A-基本项
1)平方根:Sqrt[ ],首字母大写+中括号[] -> 指令的标配。
2)Sin[Pi/2] Cos
3) Sqrt[-1] = i
4) N[exp, n] 给出exp的n位有效数字近似值
5)%调用前一次计算结果,%%再前一次,依次类推,如
Out[1] a=3
In[2] s = b+% 等价于s = b+ a
6)解方程:Solve,如Solve[x^3-2x+1 == 0]
7)多项式展开 Expand[(1+x)^10] Factor因式分解
8) Factorial[n]阶乘
9)Random伪随机数
10)Round, Floor, Ceiling, GCD, LCM, Sin Cos Tan Sec Cot Sin[Pi/3] = Sin[60 Degree]
11)Log自然对数,Log[2,100] log_2^100
12)
加Plus[a,b,c]
减Subtract
乘Times
除Divide
指数Power[a,b]
14)连乘
15)二项式
16)条件语句、循环语句
![]()
![]()
17)自定义函数(下划线)
18)序列Range[10]
19) 矩阵-花括号
B- 解方程
1)Solve[方程,变量], 1个变量时,变量可忽略。
2)多个方程式:Solve[{方程1,方程2,....},{变量1, 变量2, ...}]
3)对于超越方程,可以借助FindRoot( 本质是梯度下降 )
4)多项式化简Simplify[Expression]
C- 微分运算
1)极限运算 Limit[f(x), x->a, Direction ->1]其中Direction 可省略,1为左趋近,-1为右趋近。
2)自定义函数f,导数f',3阶导数f''',依次类推。
3)D[f[x],{x,n}]针对x求n阶导
4)多元 D[f[x,y],{x,n},{y,m}]针对x求n阶导
D- 积分运算
1)Integrate[f[x],x]
2)Integrate[f[x],{x,a,b}]
3)多重积分
E- 常微分方程
1)Dsolve[方程,y,x]
2)拉普拉斯变换
F-其他
1)添加备注:(*此处内容忽略*)
2)自然对数底是E,而不是e,区分大小写,Pi、Infinity(无穷)等等常数都是如此。
3) 搜索指令: ?*关键词*,即通配符的模糊匹配查找。
四、基本作图
暂时无此需求,用到再说。