(一)统计学习三要素:模型、策略、算法
(二)统计学习:
1.定义:基于数据建立概率统计模型并运用模型对数据进行预测和分析的学科。
2.学习:如果一个系统通过执行某个过程不断改善系统的性能,这个过程就是学习。(目前人们指的机器学习大多数是指统计机器学习)
3.统计学习的对象:数据--假设数据具有统计规律。
4.目的:考虑数据应该学习什么样的模型、如何学习模型、提高模型的学习和应用效率。
5.方法:监督学习、非监督学习、半监督学习(semi-半)、强化学习
注:首先假设数据独立同分布产生的,并且属于某个函数的集合 --假设空间(模型)
然后应用某个评价准则,选择一个最优的模型来预测数据 --模型选择的准则(策略)
最后最优模型的选取由算法决定 --模型学习的算法(算法)
6.步骤: 1-得到一个有限的数据集
2-确定包含所有可能模型的假设空间,即学习模型的集合--建立网络结构
3-实现求解最优模型的准则,即学习的策略--设置损失函数并使之最小
4-实现求解最优模型的算法,即学习的算法--随机梯度下降&&adam
5-通过学习方法选择最优模型--训练
6-应用模型进行预测、分析
7.统计学习中大数据未必是好事,过多的冗余数据对我们的学习模型造成了严重的压力,降低学习效率和效果,如果真正能做到小数据学习才是好事--作者
(三)监督学习
1.基本概念:
(1)输入空间、输出空间:所有输入和输出可能额集合--有限元素的集合。
(2)每一个具体的输入是一个实例,通常由特征向量(https://blog.csdn.net/woainishifu/article/details/76418176)表示。
矩阵乘法:m*s 与 s*n 矩阵相乘得到 m*n的矩阵。
向量:n*1维的矩阵
特征向量:如下公式所示,矩阵A乘一个向量以后等于某常数乘这个向量。那么这个向量v就是A的特征向量,这个常数就是特征值。
如一个4*4的矩阵A与4*1的向量相乘得到了4*1的向量,等同于这个4*1的向量乘一个常数N,那么N就是特征值,向量为特征向量。一个矩阵可以用特征值和特征向量表示。
具体应用场景:图片的特征值分解
2.三要素:
(1)模型:可表示为决策函数或者条件分布函数
(2)策略:
损失函数 - 01损失、平方损失、绝对损失、对数损失
(3)算法:学习模型的具体计算方法
(四)模型评估与模型选择
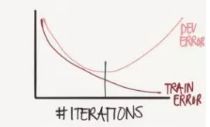
1.训练误差与测试误差
训练误差:代表了模型对训练集的学习程度
测试误差:代表了模型对未知数据的预测能力
2.过拟合与模型选择
过拟合:一味的提高模型的复杂度,以至于模型对已知数据训练的很好,但是对未知数据的预测能力较差。正如之前所说的模型过度重视了训练集中的噪点,而忽略了该有的整体趋势。
模型选择:训练误差会越来越小,测试误差会先减小后增大。模型应选择测试误差最小的点---方法正则化与交叉验证。
(五)正则化与交叉验证
1.正则化(结构风险最小化)
在经验风险最小化(预测与实际的差距)的基础上加上结构风险最小化(模型参数)。
2.交叉验证
重复的使用数据,把给定的数据进行切分,将切分的数据集组合为训练集和测试集,在此基础上反复的进行训练、测试和模型选择。
1.简单交叉验证:70训练集、30测试集。训练集各种不同的模型进行训练,测试集测试。
2.S折交叉验证:数据分为S个不想交的数据集,利用S-1个子集进行训练,剩下的进行测试。这一过程多S种选择重复进行。
3.留一交叉验证:S折交叉验证中S为训练集样本数量。比较繁琐,适用于小样本数据。
(六)泛化能力--模型对未知数据的预测能力
1.泛化误差:对未知数据的预测误差。
2.泛化误差上界
(七)生成模型和判别模型
监督学习得到的模型一般为:决策函数Y=f(x)或者条件概率分布P(Y|X)
1.生成模型:朴素贝叶斯、隐马尔科夫模型
2.判别方法:k邻近算法、感知机、决策树、逻辑回归
(八)分类问题
(九)标注问题:输入是一个观测序列(一句话),输出是一个标记序列(短语的开始、结束)--主要用于自然语言处理
(十)回归问题