Matplotlib的使用

1.pyplot基础语法

（1）创建画布
figure()创建一个空白画布，可以指定画布的大小figsize和设置分辨率dpi

plt.figure() 
plt.figure(figsize=(8,6),dpi=80) #（8，6)代表图像的长和宽单位是英寸，dpi代表分辨率

（2）创建子图
figure.add_subplot方法用来创建子图,也可以直接使用subplot.

fig=plt.figure()
fig.add_subplot(2,2,1)
或
subplot(2,2,1)
例如：
plt.figure()
x=np.linspace(-np.pi,np.pi,100)
y1=np.sin(x)
y2=np.cos(x)
plt.subplot(211)  #表示2x1的画布中的第一个
plt.plot(x,y1,'-r')
plt.title('sin')
plt.subplot(212) #等同 fig.add_subplot(212) 2x1画布中第二个
plt.title('cos')
plt.plot(x,y2,'-.b')
plt.show()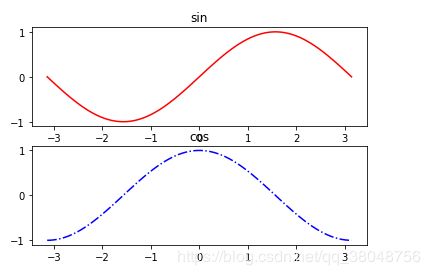

（3）添加画布内容
注意：
对于中文乱码问题，可以在作图之前添加如下代码：

plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

添加图例一定是在绘图（plot）之后，设置标签等和绘图没有先后顺序，并且图例中的顺序和绘图的顺序一致。

函数	作用
plt.title	添加标题
plt.xlabel	设置x轴的名称
plt.ylabel	设置y轴的名称
plt.xlim	设置x轴的范围（参数是上下限的tuple）
plt.ylim	设置y轴的范围
plt.xticks	设置x轴的刻度数目和取值（参数是list）【其参数rotation代表倾斜角度】
plt.yticks	设置y轴的刻度数目和取值
plt.legend	设置图例
plt.grid	设置网格线

示例（应用上面的全部设置）：

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
fig=plt.figure()
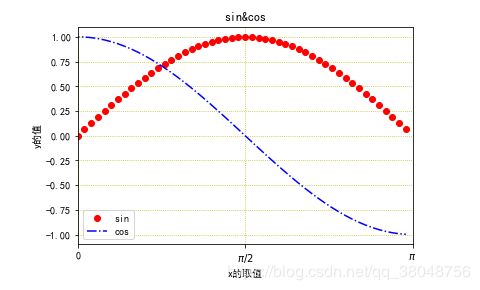
plt.title('sin&cos')
x=np.linspace(-np.pi,np.pi,100,endpoint=False)
y1=np.sin(x)
y2=np.cos(x)
plt.plot(x,y1,'-r') #实线
plt.plot(x,y2,'-.b') #虚线
a=[-np.pi,-1/2*np.pi,0,1/2*np.pi,np.pi] 
label=[r'$-\pi$',r'$-\pi/2$',0,r'$\pi/2$',r'$\pi$']  #使用laTex
plt.xticks(a,label) #设置x轴的记号，如果仅有a,则为设置x轴的ticks，其还有个参数rotation代表倾斜角度，如果x轴的刻度标签太长可以设置角度让其倾斜，例如rotation=45，代表倾斜45度
plt.xlim((0,np.pi)) #设置x轴的显示范围[0,pi)
plt.xlabel('x的取值')
plt.ylabel('y的值')
plt.grid(linestyle=':',color='y')#添加背景网格线
plt.legend(['sin','cos'],loc='lower left') #调整图例的位置在左下，注意图例中的sin,与cos对应绘图时的顺序
plt.show()

结果：

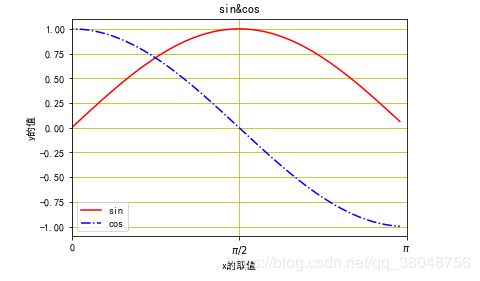
（4）保存与显示图形
savefig可以用来保存绘制的图形
show()用来显示图形

plt.savefig('1.png') #可以添加路径

2.散点图与折线图

散点图可以利用scatter函数来绘制，这个是专门绘制散点图的，也可以使用plot函数来绘制。
利用plot直接将关于连接线的部分去掉，加上marker部分就可以了就由折线图变成了散点图，对于上面例子中的：

plt.plot(x,y1,'-r')  
将其改为 plt.plot(x,y1,'ro') 就变成了散点图（用o代表点）
也可以通过scatter函数
plt.scatter(x,y1,c='r',marker='o') 

结果：

3.3D图与等高线图

对于3D图的绘制需要引入from mpl_toolkits.mplot3d import Axes3D
3D图和2D图的区别就是将x和y进行了meshgrid操作
对于meshgrid函数的作用是将x,y向量 编织成二维的栅格.
例如：
二维坐标系中X轴的取值是1，2，3，而Y轴的取值是4，5，那么可以获得（1，4）（1，5）
（2，4）（2，5）
（3，4）（3，5）这些坐标，这就构成了一个二维的网格，而meshgrid的作用就是这个。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
a=np.array([1,2,3])
b=np.array([4,5])
c,d=np.meshgrid(a,b)  #c[[1,2,3],[1,2,3]] d[[4,4,4],[5,5,5]]
e=np.array([[1,2,1],[7,8,9]])
fig=plt.figure()
#在画布上添加3D坐标轴
ax=Axes3D(fig)
#画出3d图：rstride 和 cstride 分别代表 row 和 column 的跨度，一般选择默认就行，不设置。
ax.plot_surface(c,d,e,rstride=1,cstride=1,cmap='rainbow')
ax.scatter(c, d,e, c = 'g', marker = '^') #将点标出来

结果：

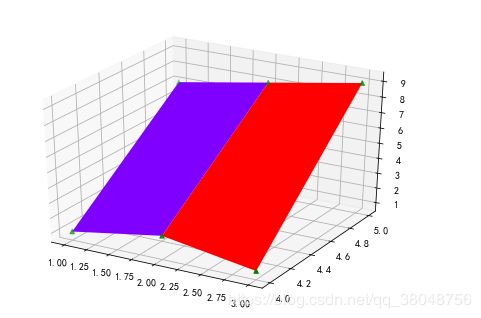
我感觉对于3D图的绘制，因为此时x轴和y轴都是二维数组，按照2d中二维数组绘图时，会对以对其进行横向分割的方式，然后去进行连接。对于3d中，首先就是根据横向分割，然后按照构成点的顺序进行连接，然后再根据纵向分割，然后按照构成点的顺序进行连接，这样就连接成了3d图。对于3D图的绘制只需要做的就是构成网格矩阵，然后根据x,y的值去求z的值，这样x,y,z全部有了后就可以对其绘制三维图。
注意：
当x和y是二维数组时，会对以对其进行横向分割的方式，然后去进行连接。

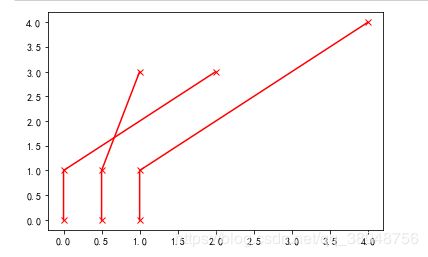
x=np.array([[0,0.5,1],[0,0.5,1],[2,1,4]])
y=np.array([[0,0,0],[1,1,1],[3,3,4]])
plt.plot(x,y,'-rx')
按照(0,0)(0,1)(2,3)连接，然后再(0.5,0)(0.5,1)(1,3)以此类推.

2D的结果：

三维的话就相当于多了个z，设z=np.array([[0,1,2],[1,2,3],[4,5,6]])
那么绘图可以理解为：
按照(0,0,1)(0.5,1,1)(2,3,4)连结,然后再(0.5,0,1)(0.5,1,2)(1,3,5)以此类推,然后再横向(0,0,1)(0.5,0,1)(1,0,2)连接，以此类推。
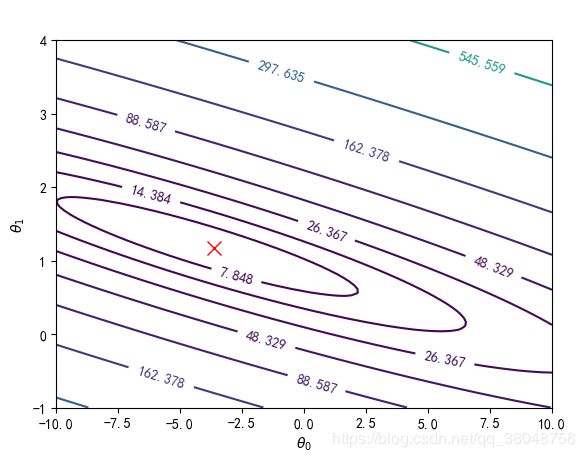
可以理解成横向分割后连接，然后再纵向分割后连接。

等高线图：

plt.figure()
plt.xlabel(r'$\theta_0$')
plt.ylabel(r'$\theta_1$')
theta0_val=np.linspace(-10,10,100)
theta1_val=np.linspace(-1,4,100)
xs,ys=np.meshgrid(theta0_val,theta1_val)
#使用contour生成三维结构表面的等值线图, np.logspace(-2,3,20)代表z值10^-2到10^3的20元素的等比数列,即那些等高线
CS = plt.contour(xs, ys, J_val, np.logspace(-2,3,20))
#最后加入Label，inline控制是否将Label画在线里面，字体大小为10。
plt.clabel(CS, inline=1, fontsize=10)
# 绘制最优解
plt.plot(theta[0,0], theta[1,0], 'rx', markersize=10, linewidth=2)
#theta[0,0], theta[1,0]为最优解的值
plt.show()

结果：